Раздел 2. Механика гибкой нити.

2.1 Аналитический расчет формы и натяжения гибких нитей.

Рис. 2.1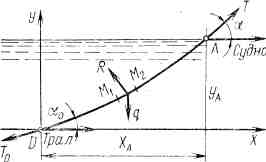

Г ибкая нить под действием сил тяжести и гидродинамического сопротивления. Большинство орудий промышленного рыболовства представляет собой пространственные сетные конструкции, оснащенные системой канатов. Для расчета формы и нагрузок, возникающих в канатах, последние рассматриваются как гибкие нити, определенным образом закрепленные и находящиеся под действием внешних сил. При определении формы и нагрузок сетных элементов орудий используются расчетные схемы, в которых сети также заменяются гибкими нитями. Для этого из сети двумя вертикальными (или горизонтальными) сечениями вырезается элементарная полоска, свойства которой аналогичны свойствам гибкой нити. Для расчета деталей орудий лова в ви­де гибких нитей используется ряд типовых расчетных схем. Одна из них имеет вид, показанный на рис. 2.1.

Дифференциальные урав­нения, описывающие форму гиб­кой нити и усилий в ней, имеют вид

(2.1)

где Т — натяжение нити в рассматриваемой точке; S — длина ни­ти; q — вес в воде нити единичной длины;  — угол, образованный касательной к нити в рассматриваемой точке и горизонталью; R_, R_n — касательная и нормальная составляющие силы сопротивления нити единичной длины.

Если нагрузка в нижней точке нити D равна нулю (T₀ = 0), то нить примет форму прямой линии, находящейся под углом  к вектору v. Значение угла в этом случае называется предельным и обозначается _Пред.

Гибкая нить сохраняет прямолинейную форму, если составляю­щие усилия Т₀, приложенного к нижнему концу, находятся в соот­ношении

To_yJT_0x=tga_Пpeд (2.2)

Таким образом, гибкая нить, закрепленная в верхней точке и находящаяся под действием сил тяжести и гидродинамического давления воды, может принять форму

прямой линии при условии _О = a= a_Пpeд;(2.3)

кривой, обращенной выпуклостью вниз, при условии о < a< a_Пpeд; (2.4)

кривой, обращенной выпуклостью вверх, при условии о > a> a_Пpeд. (2.5)

Угол атаки нити прямолинейной формы вычисляется по фор­муле

(2.6 )

где , (2.6,а )

с — коэффициент сопротивления ваера, расположенного перпен­дикулярно вектору скорости (с≈1,1); d — диаметр троса.

Нить, обращенная выпуклостью вниз (см. рис. 4), схематизи­рует форму ваера. Если пренебречь малой величиной тангенциаль­ной составляющей полного давления воды (R_x = 0), то координаты любой точки нити (ваера) вычисляются по формулам:

(2.6,б)

(2.7)

В выражениях (3.6,б) и (3.7) приняты следующие обозначения:

(2.14)

(2.15).

По формуле (2.6,6) вычисляется горизонт хода Y_А нижнего кон­ца ваера. По формуле (2.7) — расстояние по горизонтали Х_А меж­ду судном и траловой доской.

Угол атаки  любого элемента нити (ваера), в том числе в точке А крепления ваера на судне, находится по формуле

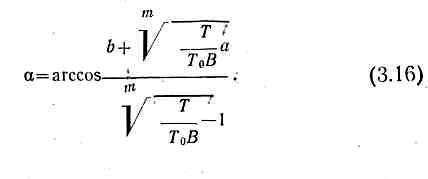
Длина гибкой нити (ваера) находится из выражения

Натяжение в нижней точке D гибкой нити (ваера) находится как

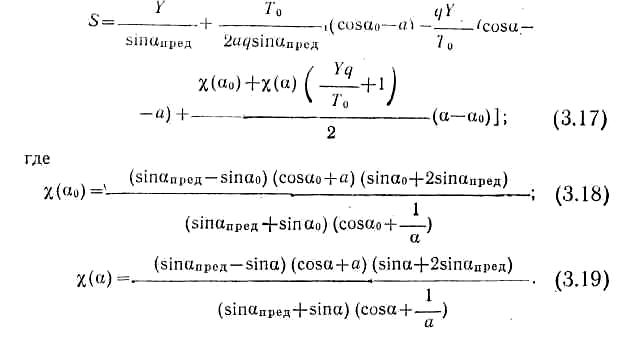
T₀ = T²оx, + T²oу. (2.20)

При расчете характеристик ваера составляющие усилия Т₀ определяются по формулам:

Тох=0,5(Rс.ч+Rос) +Rхд; (2.21)

Т₀у= (G_Д,+G_осн)-N_ГP (2.22)

г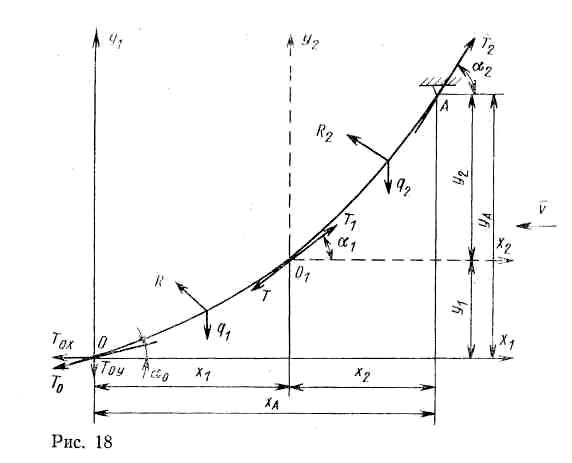 де Rсу — сопротивление канатно-сетной части трала, Н; R₀c— сопротивление оснастки подбор трала, Н; R_XД — лобовое сопротив­ление траловой доски, Н; G_осh — половина веса оснастки трала в воде, Н; в_я — вес траловой доски в воде, Н; N_ГР — реакция грун­та при движении донной траловой доски по грунту [приближенно равно (0,4-0,7) G_д].

Усилие в любой точке нити (ваера) без учета действия тан­генциальной составляющей давления воды определяется выраже­нием Рис.2.2

T = T₀+qy. (2.23)

При длине ваера более 1000 м необходимо учитывать влияние сил R_x и для расчета усилия в верхней точке ваера вместо (2.23) использовать формулу

T = T₀+qy + R_xS. (2.24)

Сила сопротивления ваера при движении в воде находится из выражения

R_b=Tcos— T_Ocos_. (2.25)

Ваер может состоять из нескольких частей, отличающихся ве­сом и диаметром троса. Расчетная схема для составного ваера показана на рис. 2.2.

Характеристики ваера в этом случае определяются поэтапно. На первом этапе рассчитываются характеристики участка ваера 00₁ для чего в качестве начальных условий ис­пользуются значения силы Т₀ и угла _O. По формулам (2.7) и (2.6,б) находятся координаты точки 0₁ — x₁ и y₁ по формуле (3.16) рас­считывается значение угла ₁ по формуле (2.17)—длина первого участка ваера S₁ по формулам (2.23) или (2.24)—усилие Т₁ в точке ваера O₁. На втором этапе рассчитываются характеристики участка ваера O₁А. При этом начальными условиями являются: Т₀=Т₁ и ₀=. По указанным формулам для второго участка на­ходятся значения х₂, у₂, ₂, S₂, Т₂. Характеристики составного вае­ра определяются как:

x_A=x₁+ x₂; (2.26)

y_а=y₁ + y₂; (2.27)

S = S₁ + S₂. (2.28)

Сопротивление составного ваера

R_B = T₂cosa₂—T_осоsа_о . (2.29)

Гибкая нить, обращенная выпуклостью вниз, схематизирует также форму сети, нижняя подбора которой закреплена на грунте.

С помощью гибкой нити, обращенной выпуклостью вверх, схе­матизируется форма деталей орудий лова, как, например, кабель сетного зонда или сеть, закрепленная у поверхности воды за верх­нюю подбору.

Замена цепной линии параболой. Для упрощения расчетов цеп­ную линию часто заменяют параболой. Гибкая нить принимает форму параболы, если внешние силы равномерно распределены по ее хорде (проекции АВ на рис. 2.3).

Уравнение параболы имеет вид

y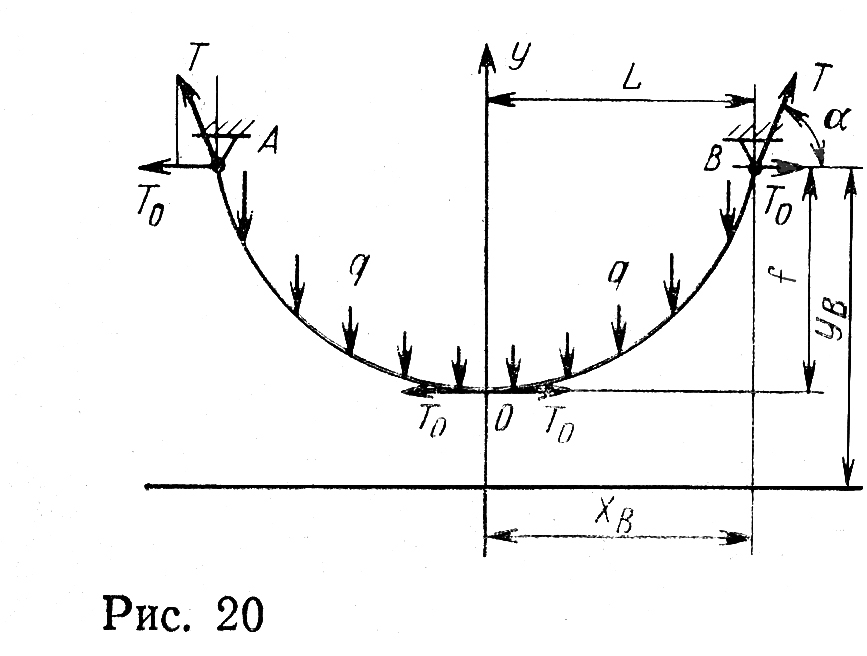 =x²/2р (3.43)

или

, x=p·tg. (3.44)

где – параметр гибкой нити.

Длина нити, имеющей форму параболы, от вершины до точки закрепления (ОА на рис. 20) приближенно может быть определе­на из выражения

Рис. 2.3

Половина хорды нити вычисляется в этом случае по формуле

(2.46)

Горизонтальная составляющая натяжения Т₀ в нити, имеющей форму параболы, находится как

T_O = qL²/2f. (2.47)

Натяжение Т в гибкой нити, как и ранее, определяется на ос­новании зависимости (2.23).

Если точки закрепления нити расположены на разных уровнях, то значение горизонтальной составляющей натяжения Т₀ зависит от взаимного расположения вершины нити и точек ее подвеса. Возможны три варианта такого взаимного расположения. Если вершина С находится между точками подвеса (рис. 2.4), то значение Т₀ будет минимальным и находится по формуле

Если воображаемая вершина нити находится вне точек подвеса, то значение Т₀ будет максимальным и определяется по фор­муле

Третий вариант имеет место, когда одна из точек подвеса совмещена с вершиной кривой. Тогда Т₀ принимает среднее значение и подсчитывается из выражения

ToСР = 2∙g∙a/y. (2.50) Силы натяжения Т в точках подвеса (рис. 2.4) определяются по формулам: (2.51) . (2.52) Если для нити, точки подвеса которой находятся на разном уровне, заданными являются значения горизонтальной состав­ляющее натяжения Т0, внешней нагрузки q, разницы абсцисс точек подвеса 2а и ординат 2b, то координаты точек подвеса, соответствующие этим значениям, могут быть вычислены по формулам:

Рис. 2.4

(2.53)

(2.54)

(2.55)

(2.56)

Учет растяжения гибкой нити. Реальные нитки, веревки и канаты существенно растягиваются под воздействием внешней нагрузки, в связи с чем возникающие в них усилия будут несколько меньше расчетных, а прогиб — больше расчетного.

С учетом растяжения гибкой нити (форма которой соответствует параболе) горизонтальная составляющая натяжения Т₀ и стрелка прогиба f находятся из выражений:

где s—относительное удлинение нити под нагрузкой.

Q = 2qL: (2.59)

Зависимость =f/(T) определяется свойствами материала, из которого изготовлена нить.

Стальные канаты подчиняются закону Гука, поэтому для них

=Т/EF; (2.60)

где Е — модуль упругости стального каната, Н/м²; F — площадь поперечного сечения каната, м².

С учетом (3.60) для стальных канатов вместо выражений (2.57) и (2.58) следует использовать:

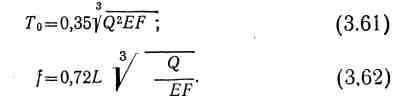
Для растительных канатов (пеньковых) можно принять

(2.63)

В связи с этим выражения для расчета горизонтальной составляющей натяжения в канате и стрелки прогиба принимают вид:

; (2.64)

. (2.65)

Гибкая нить под действием сосредоточенных сил. Если к гибкой нерастяжимой нити приложена одна сосредоточенная сила R, а точка ее приложения может перемещаться (внешняя сила приложена к кольцу, через которое проходит канат), то без учета сил трения (между кольцом и канатом) натяжения Т в ветвях нити будут одинаковыми и вычисляются по формуле

, (2.66)

где  — угол между ветвями каната.

С учетом сил трения натяжения в ветвях нити отличаются на величину силы трения. Если нить растягивается под действием со­средоточенной силы, то натяжения в ветвях снижаются по сравнению с результатом расчета по формуле (2.66). Для определения силы натяжения в этом случае необходимо знать зависимость s = f(T) для материала, из которого изготовлена рассматриваемая нить.

Гибкая нерастяжимая нить, находящаяся под действием нескольких сосредоточенных сил R₁, R₂..., различных по величине и направлению, принимаем форму многоугольника. Если точки приложения сил имеют возможность перемещаться, то без учета сил трения натяжения во всех ветвях нити будут одинаковыми и вычисляются по формуле где ₁ ₂,. — углы между соответствующими ветвями каната

, (2.67)

Вопросы для самоконтроля

1. Как определяются усилия в нитях, нагруженных сосредоточенными силами.

2. В каких случаях нить нагруженная распределённой силой принимает форму тяжелой нити? Как определить её форму и натяжение?

3. В каких случаях нить нагруженная распределённой силой принимает форму параболы? Как определить её форму и натяжение?

4. Опишите метод определения натяжения в ваере.