§ 2. Сопротивление деталей орудий лова, имеющих форму шара

Форму шара имеют, например, такие детали оснастки орудий лова, как траловые кухтыли и бобинцы, дрифтерные буи. Зависимость Cx=f(Re) для шара показана в приложении 3 [ ].

Результаты многочисленных экспериментов по определению коэф­фициента сопротивления шара показаны на рис. 1.53. На оси абсцисс нанесены значения чисел Рейнольдса, по оси ординат — значения коэффициента с.

При малых значениях числа Рейнольдса течение вокруг шара таково, что силы вязкости преобладают над силами инерции. В при­легающем к шару пограничном слое наблюдается ламинарное течение. При дальнейшем увеличении числа Рейнольдса значение инерцион­ных сил возрастает. Обтекание передней части шара остается ламинарным, но пограничный слой становится неустойчивым и отры­вается от экватора. С повышением числа Рейнольдса сверх 5·10³ происходит переход течения из ламинарного в передней части шара в турбулентное в задней части. С образованием турбулентного тече­ния изменение коэффициента с прекращается и он становится прак­тически постоянным, не зависимым от числа Рейнольдса, на участке примерно до Re = 2·10⁵. Эта область сравнительно постоянных ко­эффициентов с называется автомодельной.

	Рис. 1.5. Результаты экспериментов по определению коэффициентов сопротивления: 1 — шара; 2 — пластин; 3 — цилиндра.
5·10 102 103 104 105 Re 106

При Re = 2- 10^б точка перехода ламинарного слоя в турбулент­ный отодвигается назад по потоку, из-за чего распределение давле­ния приближается к идеальному и коэффициент с резко падает («кризис»).

Форму шара имеют поплавки и грузила различного диаметра (от d = 0,01 до d = 0,8 м). Скорость движения их в воде колеблется от v = 0 до v = 3,0 м/с. При величине диаметра до 0,2 м и скорости до 2 м/с значения коэффициента с остаются постоянными (с = 0,45 -f-— 0,5). При больших значениях d и v, что характерно, например, для'тралового лова (кухтыли, бобинцы), значения коэффициента с могут оказаться в зоне кризиса сопротивления.

Число Re подсчитывается из соотношения

(1.24)

где d — диаметр шара, м;  — коэффициент кинематической вязкости воды, м²/с.

Данные о коэффициентах кинематической вязкости морской воды в зависимости от температуры и солености приведены в приложении 2.

Сопротивление деталей орудий лова, имеющих форму пластины.

Форму пластины имеют, например, такие детали оснастки орудий лова, как траловые распорные доски и подъемные щитки.

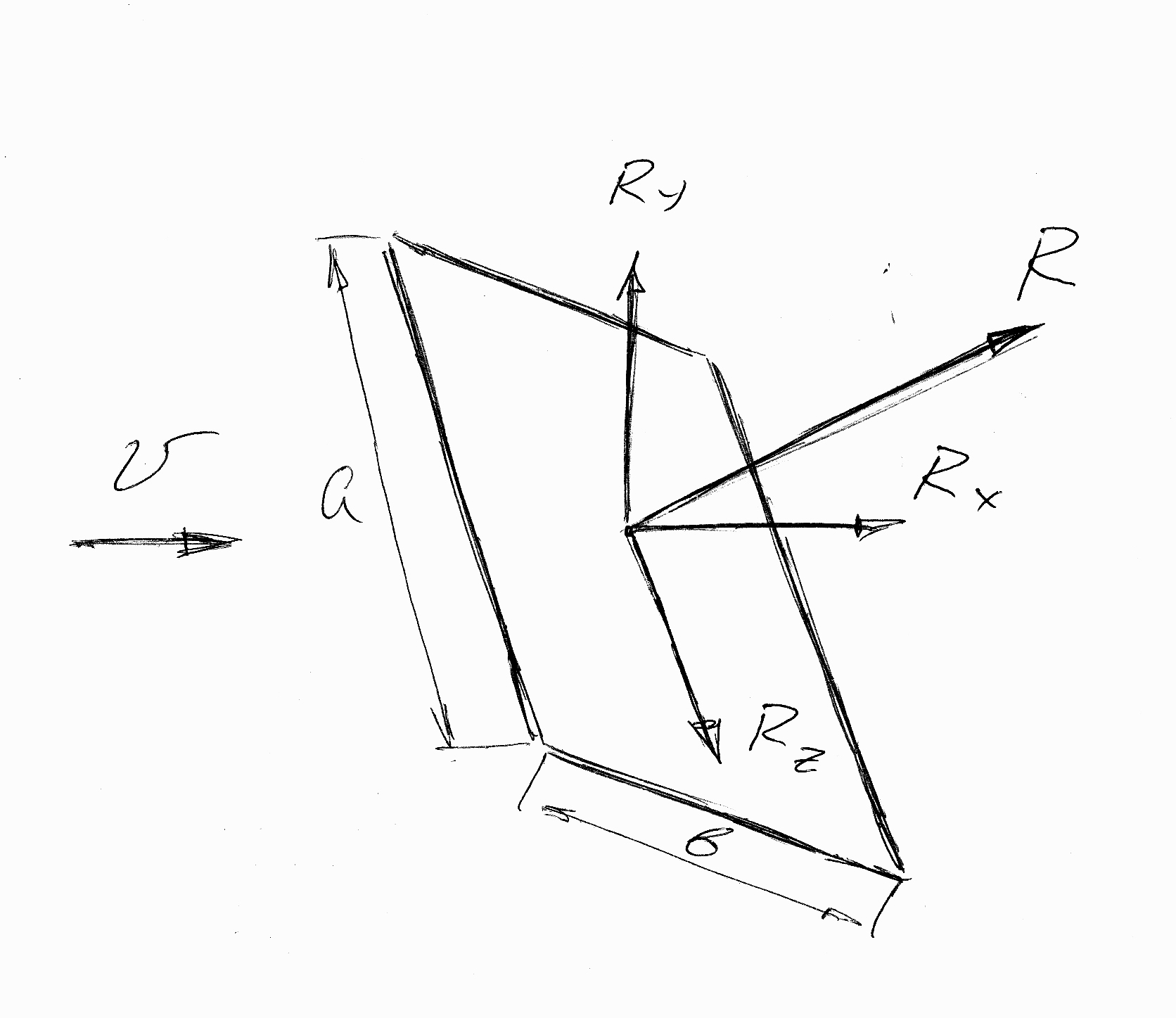
Рис. 1.6. Проекции вектора равно­действующей сопротивления плас­тины на координатные оси.

Для пластины, расположенной под некоторым углом  к направлению движения, результирующая гидродина­мических сил R может быть разложена на составляющие: силу лобового сопротивления R_x, подъемную (или распорную) силу R_y, боковую силу R_z.

Точка приложения равнодействующей сил сопротивления (центр давления) при изменении угла а лежит на продольной оси симметрии пластин между передним ее ребром и поперечной осью симметрии.

Значения составляющих рассчитываются по формулам:

где с_х, с_у, c_z — гидродинамические коэффициенты этих сил.

(1.25)

(1.26)

(1.27)

Отношение cу/с_х, т.е. коэффи­циентов подъемной силы и лобово­го сопротивления, называется гидродинамическим качеством. Гидродинамическое качество k пластины определяется из от­ношений:

k=Cylc_x=R_y/R_X: (1.28)

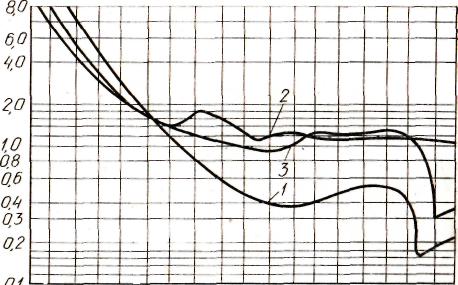
Его ве­личина имеет максимальное значение при малых углах атаки. В ка­честве примера на рис. 17 показана зависимость гидродинамического качества пластины от угла атаки при X = 0,5.

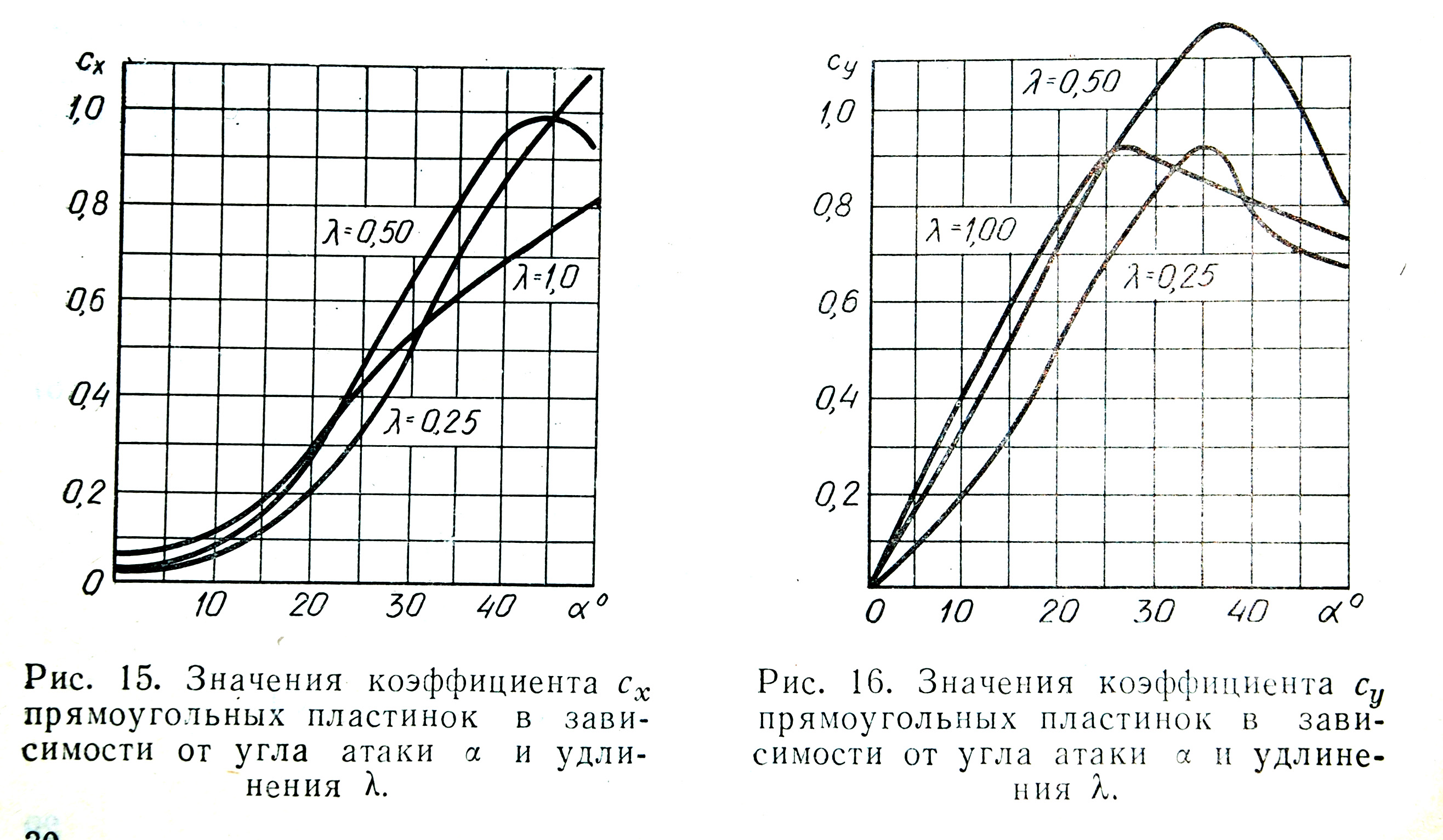
Значения коэффициентов с_х и с_х для некоторых прямоугольных пластин в зависимости от угла а и удлинения X приведены на рис. 1.7 и 1.8.

Рис. 1.7. Значения коэффициента сх прямоугольных пластинок в зави­симости от угла атаки  и удли­нения 	Рис. 1.8. Значения коэффициента су прямоугольных пластинок в зави­симости от угла атаки а и удлине­ния

В общем случае для пластины любой формы удлинением назы­вают отношение

(1.29)

где а размах; F — площадь пластины

Значения коэффициента лобового сопротивления с_х для квадратной или круглой пластины, плоскость которой расположена пер­пендикулярно направлению движения, в зависимости от числа Рейнольдса показаны в приложении 6. Удлинение пластины находится из выражения

=a²/F. (1.30)

Для прямоугольной пластины

 =а/b, (1.31)

где а – размах пластины; b – ее хорда.

Коэффициент центра давления C_d1 находится из отношения

C_d1=х_1d/b, (1.32)

где х_1d — расстояние между передним ребром пластины и центром давления.

Вектор результирующей гидродинамических сил R в общем случае не проходит через начало координат и создает моменты относительно осей X,Y,Z. Момент M_z (относительно оси Z) находится из выражения

(1.33)

где т_г — коэффициент гидродинамического момента.

Зависимости указанных гидродинамических коэффициентов от угла атаки для профилированных пластин индивидуальны для каждого профиля пластины и ее формы в плане.

Связь между значениями гидродинамических коэффициентов определяется выражением

(1.34)

Сопротивление пластины, параллельной течению, целиком обус­ловлено силами трения и находится по формуле

(1.35)

где Cf — гидродинамический коэффициент трения

Коэффициент трения Сf зависит от числа Рейнольдса.

Для ус­ловия Re<10⁴ (1.36)

Для условий 10⁶<Re<2*10⁷ c_f=0,074/Re^1/5 (1.37)

В диапазоне. 10⁴ <Re<10⁶ коэффициент c_f принимает промежуточные значения.

В соотношениях (1.36) и (1.37) число Re находится как

(1.38)

Для расчета сил трения также используются формулы: для условия Re<10⁴

R= 0,7b ^-0,57Fv ^1,5 (1.39)

и для условия 10⁶<Re<2*10⁷

R=2,3b^-0,2Fv ^1,8 (1.40)

Расчет подъемной силы R_y и силы лобового сопротивления R_x гидродинамических щитков, применяемых для оснастки тралов, аналогичен изложенным выше расчетам для пластины.

Для оснастки орудий лова применяются также тела и более сложных форм, чем рассмотренные выше (стяжные кольца кошелькового невода, поплавки и грузила в виде цилиндров с закругленными или конусообразными концами и т. д.).

Сопротивление деталей орудий лова, имеющих форму цилиндра.

Форму цилиндра имеют поплавки и грузила, применяемые для оснастки подбор кошельковых неводов, закидных неводов, плавных и ставных сетей. Близки к цилиндрической форме прямолинейные тросы, канаты и нитки.

Гидродинамические коэффициенты для цилиндра зависят от формы его сечения (круг, эллипс ...), Re, удлинения  (отношения длины l к диаметру d), угла атаки .

Для кругового цилиндра значения гидродинамических коэффициентов находятся в три этапа. Сначала находится значение коэффициента Cб.у для цилиндра бесконечного удлинения (>40) при расположении оси цилиндра перпендикулярно вектору скорости набегающего потока в зависимости от числа Рейнольдса. Зависимость Cб.y=f(Re) для цилиндра с круговым сечением показана в прило­жении 4. Re определяется из соотношения (1.24). Далее уточняется значение гидродинамического коэффициента с учетом его фактиче­ского удлинения:

Ск._У=С_б._уk(λ). (1.41)

Данные о поправочном коэффициенте k() приведены в приложении» 5. Затем находятся гидродинамические коэффициенты подъемной силы с_у и лобового сопротивления с_х в зависимости от угла атаки :

C_Y = C_КY.sin²cos; (1.42)

C_Х = C_KYsin². (1.43)

Ориентировочные значения коэффициентов сопротивления для цилиндров бесконечного удлинения при расположении оси перпендикулярно вектору скорости набегающего потока: для эллиптического сечения Сб.у=0,2; для цилиндра, имеющего в сечении форму тела наилучшего обтекания, Сб.у=0,026.

Качественно сопротивление прямолинейных тросов, канатов и ниток подчинено тем же закономерностям, что и сопротивление гладких цилиндров. Количественно значения гидродинамических коэффициентов этих тел отличаются существенно. Поэтому значения коэффициентов для цилиндра могут использоваться лишь в ориентировочных расчетах гидродинамических сил, действующих на пря­молинейные тросы, канаты и нитки.

Гидродинамические коэффициенты для прямолинейных стальных тросов, расположенных под углом а к потоку, могут быть найдены по формулам:

(1.44)

c_У=asin²cos; (1.45)

c_Z = ±bsin³cos, (1.46)

где C₉₀ — коэффициент сопротивления троса, ось которого располо­жена перпендикулярно направлению движения, его значение может быть принято равным 0,9—1,15; C_O — коэффициент сопротивления троса, ось которого совпадает с направлением движения, его зна­чение находится в пределах 0,02—0,03; а - эмпирический коэффи­циент, равный 0,92; b - эмпирический коэффициент, значение кото­рого зависит от диаметра троса следующим образом:, для тросов диаметром 18—20 мм b = 0,65; для тросов диаметром 20—25 мм b = 0,65-1,0; для тросов диаметром больше 25 мм b = 1,0.

Формула (1.46) справедлива для стальных шестипрядных тросов. Знак «минус» здесь относится к тросам правой свивки, знак «плюс» — к тросам левой свивки. Таким образом, направления бо­ковой силы R_z для тросов правой и левой свивок противоположны.

Характерную площадь F в этом случае следует вычислять как про­изведение хорды и диаметра каната.