Контрольные вопросы.

1. Охарактеризуйте двухмерные расчетные модели траловых систем.

2. Охарактеризуйте трёхмерную расчетную модель В.И.Габрюка.

3. Охарактеризуйте трёхмерную расчетную модель А.В.Дверника и Г.М. Долина.

4. Охарактеризуйте трёхмерную расчетную модель В.П. Карпенко.

5. Охарактеризуйте трёхмерную расчетную модель с раздельным изображением голых концов.

6. Опишите алгоритм оптимизации размеров траловой системы.

7. Что представляет собой симплексный метод нахождения экстремума функции.

4.2. Механика кошельковых неводов

Теоретическая модель лова рыбы кошельковым неводом

В соответствии со схемой В. А. Ионаса допустим, что кошельковым неводом обметано некоторое водное пространство , где имеется n_O рыб. Во время выполнения последующих промысловых операций рыба выходит из невода со скоростью v_P через ворота площадью S. Пусть к рассматриваемому нами моменту времени из невода уже ушло п₁ рыб. Тогда концентрация ₁ рыбы в неводе к этому моменту будет

(4.1)

За элементарный промежуток времени dt из невода уходит dn₁ рыб, причем dn₁=₁Sv_Pdt

где  — вероятность выхода рыбы (0 ≤  ≤ l)

Подставляя сюда в это равенство выражение (4.1), после ин­тегрирования получим, что количество ушедших из невода рыб к дан­ному моменту времени будет

(4.2)

Пусть, например, t есть момент полного закрытия ворот. Тогда оста­ток рыбы в неводе, т. е. улов п = n_Q — n_L, определится как

(4.3)

Первоначальное количество рыб в неводе было п₀ = , где  — первоначальная их концентрация в обметанном объеме.

Этот объем можно представить в функции от главных размеров не­вода —его длины L и высоты Н. Если замет выполнен по окружности радиуса R, а высоту Н полагать постоянной, то

(4.4)

Тогда

(4.5)

Таким образом, получено, что величина улова зависит от трех био­логических параметров рыбы (, , v_P), трех технических параметров невода (L, H, S) и времени t, которое зависит также и от параметров сейнера.

Из выражения (4.5) следует очевидная и без анализа линей­ная зависимость улова п от концентрации рыбы р. Зависимость п от L и H в действительности, конечно, сложнее, так как распределение рыбы в водном пространстве обычно неравномерно, а размеры самих скопле­ний ограничены. Влияние на величину улова параметров , S, v_P и t одинаково.

С помощью выражения (4.5) можно найти выражение для коэф­фициента абсолютной уловистости кошелькового невода ср. Учитывая, что по определению  = п/п₀, получим

(4.6)

Определение длины кошелькового невода

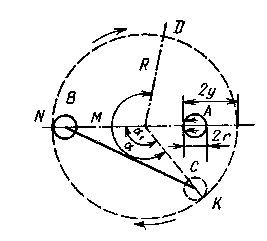
Рис. 4.14 Расчетная схема замета невода для лова тихоходных рыб

Схема лова тихоходных рыб. При определении минимальной длины кошелькового невода принимают во внимание главным образом факто­ры, действующие в процессе его замета. Во время замета различают две основные ситуации: либо косяк, наткнувшись на стенку невода, поворачивает в сторону ворот, чтобы выйти между клячами, либо об­метанный косяк, обнаружив стенку невода, погружается, чтобы уйти под нижнюю подбору. Заранее нельзя сказать, какой способ ухода изберет рыба, поэтому даже при облове стай одного и того же вида необходимо предусматривать возможности обеих ситуаций.

На рис. 4.14 показана расчетная схема замета невода для лова срав­нительно тихоходных рыб, движущихся со скоростью порядка 0,1 — 0,2 м/с.

Предположим, что косяк рыбы продольного размера 2r с центром в точке А движется со скоростью v_P. Замет начинается из некоторой точки К по окружности радиуса R, центр которой находится на линии движения рыбы. Допустим, что к моменту подхода головы косяка к

стене невода судно уже находится в точке D, причем скорость его дви­жения v_c.

За время, в течение которого судно проходит путь KD = R,косяк

пройдет путь АВ, причем

(4.7)

Отношение скоростей судна и рыбы (обозначим его ) пропорцио­нально отношению путей, проходимых судном и косяком за один и тот же промежуток времени, т. е.

 = v_C/v_P = KD/AB = R/2(R—у), откуда (4.8)

Наихудшим случаем для ситуации, когда косяк ищет выхода через ворота невода, будет такой, когда косяк, наткнувшись на стенку не­вода в поисках выхода, повернет из точки В прямо к точке К- Чтобы закрыть путь рыбе, судно должно успеть замкнуть окружность, т. е. пройти расстояние DK.

Путь косяка будет ВС =2(R — r)sin_, а путь судна за это время составит DK. = (2 — )R, поэтому отношение скоростей судна и ры­бы выразится как  = v_C/v_P = (2 — )R /2(R — r) • sin  ₁/2, откуда

(4.9)

Из сравнения выражений (4.7) и (4.8) получим

(4.10)

(4.11)

Рассмотрим случай, когда косяк пытается уйти под низ невода. Допустим, что когда невод выметывается в точке N (см. рис. 4.14), косяк подошел в точку М. Следовательно, за одно и то же время путь косяка будет AM, а путь судна KN, т. е. AM = v_Pt, KN = v_ct =Ra₁. Тогда  = v_C/v_P = KN/AM. Путь, пройденный рыбой, AM =Ra₁/ , а дистанция между судном и косяком ВМ = А В — AM = 2(R — у) — Ra₁/.

Пусть время, в течение которого нижняя подбора погрузится на достаточную глубину, равно t₀, тогда при скорости погружения рыбы v_П.Р величина ВМ должна быть больше или равна v_П.Рt_O.

Обозначим опережение косяка судном ВМ — v_П.Рt_O, тогда

(4.12)

и соответственно (4.13)

Схема лова быстроходных рыб. Схема лова подвижных рыб, когда  = 3÷5, основана на том, чтобы «закружить» косяк (рис. 191). Когда это удается, косяк при встрече со стеной невода продолжает двигаться вдоль нее и стремится уйти под невод.

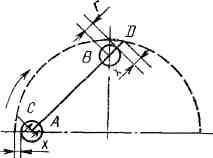
Рис. 4.15. Схема лова бы­строходных рыб.

Замет начинают из точки С, чтобы пересечь направление движения рыбы в точке D на некотором расстоянии х от головы косяка. За одно и то же время путь судна CD = R/2, а путь рыбы AВ = (R — х —r) . Поэтому отношение скоростей хода судна и дви­жения рыбы будет  = CD/A В = R/2 (R — х — r), откуда

(4.14)

Вопросы для самопроверки.

1. Как теоретически оценить процент рыбы, пойманный неводом?

2. Схемы замёта кошелькового невода в зависимости от скорости хода рыбы.

3. Как зависит длина требуемого невода от скорости рыбы?