- •Курс – 3
- •Содержание
- •Введение
- •Тематический план дисциплины.
- •Раздел 1. Внешние силы, действующие на орудия лова
- •1.1 Силы веса и трения; усилия, развиваемые рыбой
- •1.2 Гидродинамические силы
- •§ 2. Сопротивление деталей орудий лова, имеющих форму шара
- •Сопротивление канатов и ниток
- •Сопротивление объёмных сетей.
- •1.3. Тяговые характеристики судов
- •Фактическая тяга судна определяется по зависимости:
- •Раздел 2. Механика гибкой нити.
- •2.1 Аналитический расчет формы и натяжения гибких нитей.
- •2.2 Графостатический расчет формы и натяжения гибких нитей, канатов и сетей
- •Вопросы для самоконтроля
- •Раздел 3. Механика сетей
- •3.1 Геометрия и статика рыболовных сетей
- •3.1.1. Общие свойства рыболовных сетей
- •3.1.2. Статика плоской рыболовной сети
- •2.3. Сетные оболочки
- •Раздел 4. Механика основных орудий лова
- •Механика тралов Расчетные схемы траловых систем.
- •4.1.1. Двухмерные схематизации траловой системы.
- •Трёхмерные схематизации траловой системы.
- •Описание входных параметров.
- •Алгоритм расчета конфигурации траловой системы.
- •Контрольные вопросы.
- •4.2. Механика кошельковых неводов
- •4.3. Механика дрифтерных порядков Форма сетей во время лова
- •4.4 Механика ярусов
- •4. Выбор каната для хребтины
- •4.5. Физическое моделирование орудий лова
- •Перечень литературы
- •Тираж __________ экз. Подписано к печати ______________________.
2.3. Сетные оболочки
Рис.
3.19. Криволинейный элемент
произвольной пространственной
сети.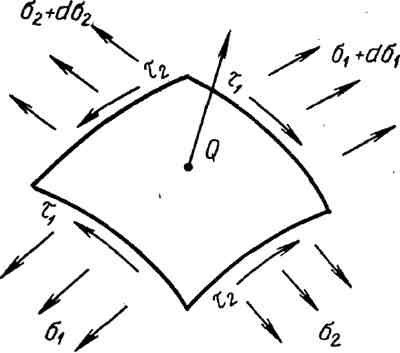 собенности
расчета сетных оболочек. Общие уравнения
равновесия рыболовной сети
произвольной формы составлены А. И.
Зоновым. Для этого рассматривается
элементарный криволинейный четырехугольник
(рис. 3.19), стороны которого совпадают
с диагональными, линиями ячей сети,
нагруженной некоторой внешней
силой Q.
На кромках сети,
помимо нормальных напряжений ,
возникают в общем случае и касательные
напряжения .
Расчет сетной оболочки осуществляется
путем решения системы дифференциальных
уравнений равновесиями использования
некоторых геометрических соотношений.
Ограничим рассмотрение
существующих методов расчета
только некоторыми вопросами,
относящимися к сетям типа сетной
оболочки вращения. При определенных
допущениях к таким оболочкам можно
отнести сети тралов, кошельковых неводов
и других орудий лова. Так, например,
в качестве исходной для трала можно
рассматривать сетную оболочку, посаженную
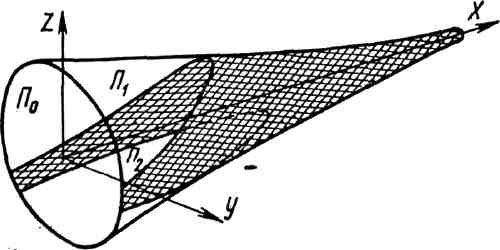
на круглый обруч П0 (рис. 3.20). Рассчитав
исходную оболочку, т. е. определив ее
размеры, раскрой, ассортимент делей и
нагрузки в нитях, затем отрезаем излишние
сети по назначенным линиям подбор
П1 и П2. Действие отброшенных сетей
заменяем соответствующими усилиями
оснастки, приложенными к подборам П1 и
П2.
собенности
расчета сетных оболочек. Общие уравнения
равновесия рыболовной сети
произвольной формы составлены А. И.
Зоновым. Для этого рассматривается
элементарный криволинейный четырехугольник
(рис. 3.19), стороны которого совпадают
с диагональными, линиями ячей сети,
нагруженной некоторой внешней
силой Q.
На кромках сети,
помимо нормальных напряжений ,
возникают в общем случае и касательные
напряжения .
Расчет сетной оболочки осуществляется
путем решения системы дифференциальных
уравнений равновесиями использования
некоторых геометрических соотношений.
Ограничим рассмотрение
существующих методов расчета
только некоторыми вопросами,
относящимися к сетям типа сетной
оболочки вращения. При определенных
допущениях к таким оболочкам можно
отнести сети тралов, кошельковых неводов
и других орудий лова. Так, например,
в качестве исходной для трала можно
рассматривать сетную оболочку, посаженную
на круглый обруч П0 (рис. 3.20). Рассчитав
исходную оболочку, т. е. определив ее
размеры, раскрой, ассортимент делей и
нагрузки в нитях, затем отрезаем излишние
сети по назначенным линиям подбор
П1 и П2. Действие отброшенных сетей
заменяем соответствующими усилиями
оснастки, приложенными к подборам П1 и
П2.
|
|
Рис. 3.20. Исходная сетная оболочка для трала.
|
Рис. 3.21. Поверхность вращения, на которую нужно наложить сеть. |
Рассмотрим некоторую поверхность вращения (рис. 3.21), да которую нужно наложить сеть. Для однозначного определения требуемой формы сети необходимо зафиксировать посадку ее вдоль параллели П0 и меридиана М, т. е. задать и0 и им = f(s), где s — длина меридиана. Задание требуемой посадки иM вдоль меридиана можно осуществить, пропустив вдоль него канатную подбору.
Такая сеть будет иметь правильную структуру (без изломов), если диагональные линии ятей будут направлены соответственно по меридианам и параллелям оболочки (т. е. диагональные линии являются линиями кривизны поверхности).
Упрощенная расчетная схема. При обосновании упрощенных методов расчета сетей введены следующие допущения: сеть имеет вид поверхности вращения, диагональные линии ячей совпадают с параллелями и меридианами поверхности, неравномерность размера ячей отсутствует, размер ячей весьма мал по сравнению с размерами сети, сетные нити нерастяжимы.
П
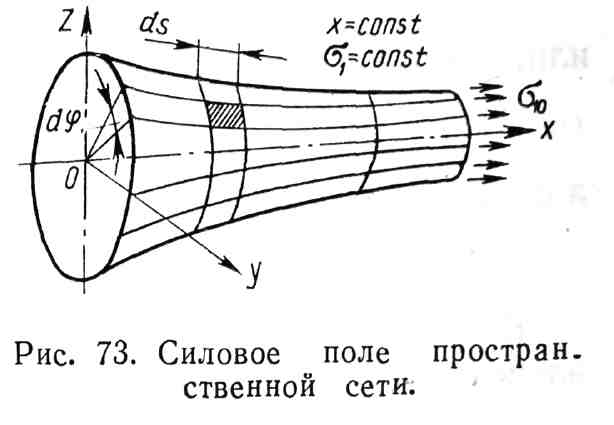
Рис
3.22 Силовое поле пространственной сети
Линии уровня поля = const совпадают с параллелями, а изменение
 градиента
поля происходит вдоль меридианов.
градиента
поля происходит вдоль меридианов.
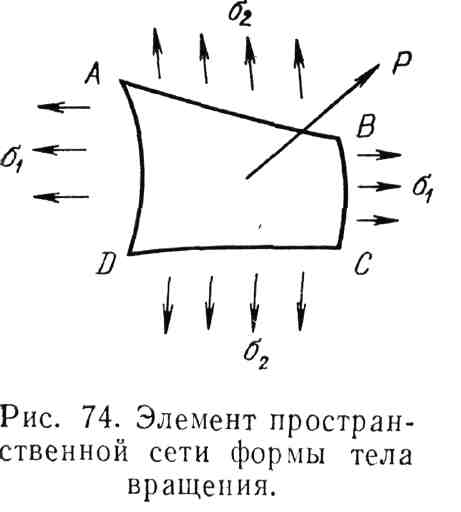
На поверхности сети выделим двумя меридианами узкую Полоску шириной dy, а на ней — участок длиной ds. Действующие на выделенный элемент ABCD внешние гидродинамические силы Р уравновешиваются внутренними усилиями по его кромкам x и y (рис. 3.23). Суммарное внутреннее усилие по кромке AD есть
Тм=xrd, (3.48)
где r — радиус параллели кромки.
|
|
Рис 3.23 Элемент пространственной сети формы тела вращения |
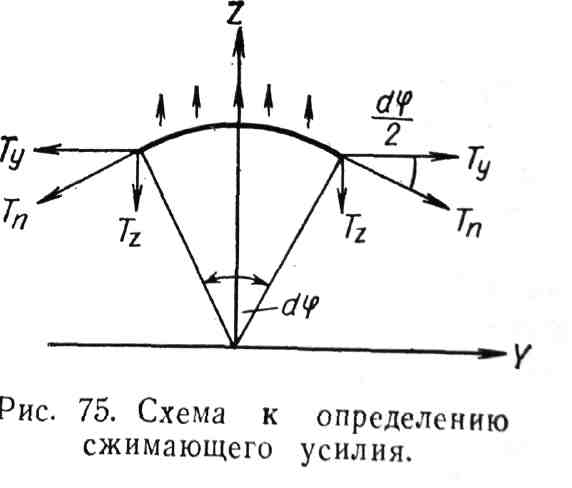
Рис 3.24 Схема к определению сжимающего усилия |
Суммарное внутреннее усилие покромке АВ будет
Tn=yds. (3.49)
Внутренние силы ТП, действующие по параллелям, вызывают некоторое сжимающее усилие ТZ, направленное по оси Z. На рис. 3.24 видно, что составляющие ТY взаимно уравновешиваются, а сумма составляющих Tz дает силу
Tz = 2TПsin(d/2)
или, учитывая, что величина d мала,
Tz = 2TПd
а с учетом выражения (3.43) Tz = xdds. (3.50)
Внешняя гидродинамическая сила Р, действующая на выделенный элемент сети, может быть представлена как
P = pdF
Или P = pr d ds. (3.51)
Если представить ее состоящей из двух компонент: рx — по оси X и py — по радиусу r, то
Px = pxr d ds, (3.52)
Рy = pyr d ds.
Полоску сети шириной rdy можно заменить гибкой нитью — плоским эквивалентом пространственной сети и ее силового поля, который представляет собой меридиональное сечение поверхности сети. Для этого умножим все силы на коэффициент k = 1/d и с учетом этого определим силы, действующие на единицу длины гибкой нити.
Натяжение нити по выражению (3.48) будет
![]() (3.53)
(3.53)
Сжимающее усилие по выражению (3.50) будет
![]() (3.54)
(3.54)
Это усилие, являющееся для нити внешним, для сети будет внутренним и на нее не действует. Составляющие внешней гидродинамической силы, приложенной к элементу нити, с учетом выражения (3.52) будут
![]() (3.55)
(3.55)
![]() (3.56)
(3.56)
Схема приложения этих сил показана на рис. 3.25.
Рассматриваемая гибкая нить — плоский эквивалент сети — имеет особое свойство: ее длина, как и величина действующих на нее внешних| сил, зависит от формы ячеи в сетной оболочке. Так, например, выражение (3.54) можно представить как
qC = y=xtg2
или с учетом выражения (3.53)
![]() (3.57)
(3.57)
-
где — угол, определяющий форму ячеи сети.
Длина элемента гибкой нити ds связана с длиной сети в жгуте dl очевидным соотношением
ds = dl cos , (3.58)

что позволяет учесть в расчетах необходимое изменение длины эквивалентной нити.
Рис- 3.25. Равновесие нити — плоского эквивалента сети.
Уравнения равновесия. Уравнения равновесия гибкой нити — плоского эквивалента сетной оболочки — в проекциях на натуральные оси и n будут
![]()
![]() ,
(3.59)
,
(3.59)
где Fx и Fy — проекции внешних сил соответственно на направления касательной и нормали; Ry — радиус кривизны гибкой нити.
Натяжение T определяется по формуле (3.53). Проекции внешних сил имеют вид
Fx = qx cos + (qC — qy) sin , (3.60)
Fy = qx sin + (qC — qy) cos ,
где — угол, определяющий направление оси относительно оси X или соответственно оси п относительно оси Y.
Различные решения уравнений (3.59) будут зависеть от конкретного вида функций F1 и F2, которые сложным образом зависят от формы сети, формы и размеров ячеи и от ряда задаваемых дополнительных условий или требований к форме сети, ее раскрою, посадке и натяжениям в нитях. Дополнительные условия вводятся в дифференциальные уравнения. Их решения получают, как правило, с помощью ЭВМ. Задачи расчета оболочки произвольной формы являются еще более сложными и достаточных решений пока не имеют.
Определение формы сети графоаналитическим методом. Для случая, когда сеть имеет форму тела вращения, вид кривой ее меридиального сечения можно получить графоаналитическим методом.
На рис. 3.26 кривая АО'В — меридианное сечение сетной поверхности плоскостью, проходящей через ось вращения X. Внутреннее давление отсутствует. Сеть посажена на два обруча. Один из них закреплен, а второй нагружен осевой силой.
Пусть в некоторой точке С' поверхности главные радиусы кривизны будут r1 и r2. Соотношение их можно определить при помощи одного
Рис
3.26 Меридианное сечение сети, посаженной
на обручи
из основных уравнений равновесия сетной оболочки произвольной формы:
![]() (3.61)
(3.61)
При отсутствии внутреннего давления Q = 0 и
![]() (3.62)
(3.62)
Искомую кривую А В получим как сопряжение большого числа малых дуг, проводимых соответствующими радиусами r1. Точность построения тем выше, чем меньшей длины будут эти дуги. Величина r1 определится из выражения (3.62):
![]() , (3.63)
, (3.63)
а с учетом выражения (3.29) получим
 (3.64)
(3.64)
Для начала построения необходимо знать величину желаемого радиуса окружности г2 и коэффициента посадки и2 в наиболее узком месте тела вращения. Если ось X совместить с осью вращения, а начало координат поместить так, чтобы ось Y проходила через сеть в наиболее узком месте, то величина r2 будет равна радиусу окружности в этом сечении (r2 = у), причем оба радиуса кривизны r1 и r2 лежат на оси ординат. Значение и2 легко определить из равенства
sy и2 = 2паи2 = 2у (3.65)
где sy — ширина сетного полотна в жгуте; п — число ячей по ширине; а — шаг ячеи.
Отсюда
![]() (3.66)
(3.66)
Построение
ведем следующим образом. На оси ординат
(рис. 3.27) отмечаем
точку A,
где r2
= у —
желаемому радиусу наиболее суженной
части сети. Затем по формуле (3.57) определяем
r1
и,
откладывая
его
на оси Y,
находим
центр кривизны В.
Отсюда
радиусом r1
описываем
малую дугу АА’.
Если
теперь провести из точки B
через точку
А’ прямую
до пересечения с осью X,
то новое значение r2'
будет равно A’O’,
а
новое значение у1
будет
А'А1’.
Подставляя
его в выражение (3.66), находим
значение и'2,
а затем с помощью выражения (3.64) находим
значение
r’1
для
следующей малой дуги искомой кривой.
Откладывая от
точки А'
отрезок
r’1,
н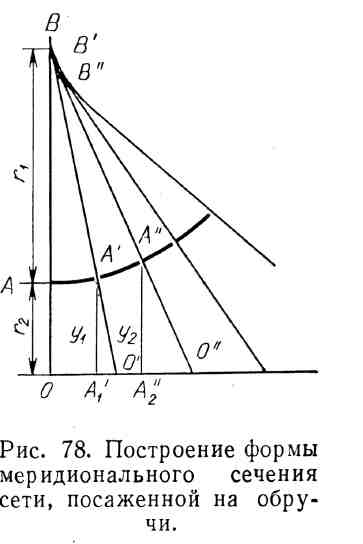 айдем
точку В'—
новый центр кривизны. Из точки В'
радиусом
r’1
описываем следующую малую дугу А’
А” и т. д.,
постепенно строим один квадрант
меридионального сечения сети.
айдем
точку В'—
новый центр кривизны. Из точки В'
радиусом
r’1
описываем следующую малую дугу А’
А” и т. д.,
постепенно строим один квадрант
меридионального сечения сети.
К
Рис
3.27 Построение формы меридианного
сечения сети, посаженной на обручи
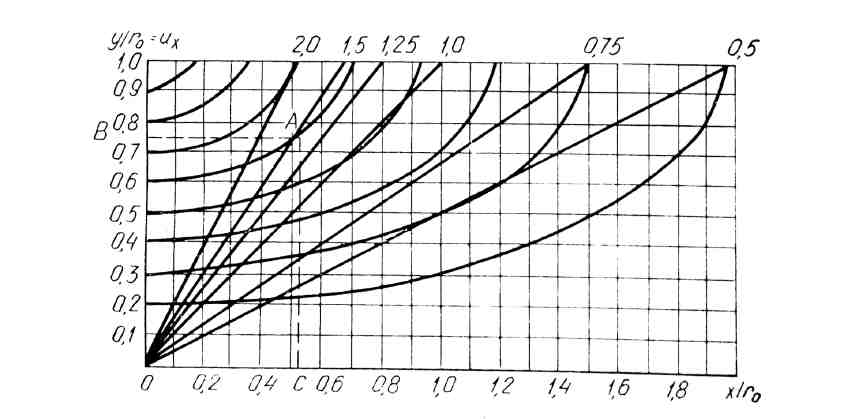
Расстояние между обручами L = 2х/r0 определяют по графику из соотношений L/r = 2AB/AC, L = 2r·0,55/0,76 =1,5r, где r — радиус обруча. Наклонные прямые на графике соответствуют различным соотношениям r/(L/2) = D/L.
|
Рис. 3.28. Форма меридионального сечения сети, посаженной на обручи в зависимости от расстояния между обручами и посадочного коэффициента. |
Практически часто нужно знать требуемые размеры сетного полотна в жгуте sx и sy для постройки сети (например, секция вентеря) требуемой формы. Зависимости между размерами сетей в жгуте и размерами их после прикрепления к обручам приведены в работе Н. Н. Андреева «Проектирование кошельковых неводов».