3.1.2. Статика плоской рыболовной сети

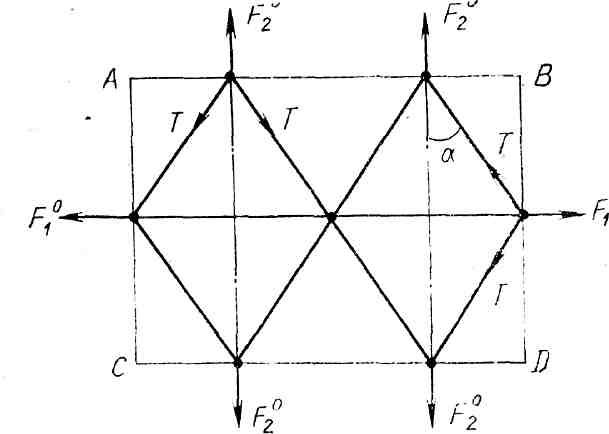
Соотношения сил, растягивающих ячею сети. Чтобы определить основные силовые соотношения для плоской сети, предположим, что сеть ABCD (рис. 3.8) состоит всего из двух ячей. Сеть растянута внеш­ними силами F₁^O и F₂^O, которые приложены к узлам и направлены вдоль диагоналей ячей. Они уравновешиваются натяжениями в ни­тях Т.

Из условий равновесия узлов получаем

F₂^O = 2Tcos,

F₁^O =2Tsin,

откуда

F₂^O = F₁^O ctg. (3.26)

Теперь увеличим число ячей сети по каждой стороне в k раз, а шаг их пропорционально уменьшим в k раз. Тогда внешние усилия,, растягивающие ячею уменьшенных размеров вдоль ее диагоналей. F₂ и F₁ будут

F₂ = F₁ ctg.

Сравнивая выражения (3.27) и (3.26), видим, что соотноше­ние сил F₂ и F₁ не зависит от размера ячеи.

Положим, что шаг ячеи сети бесконечно мал, а число ячей бес­конечно велико (непрерывная мoдель сети). Из-за малого шага ячеи можно считать, что по кромкам идеализированной сети внешние силы распределены равномерно. Тогда в пределах одной ячеи с достаточно. малыми диагоналями x: и у напряжения будут

и

^{Их соотношение поэтому выразится как}

а с учетом соотношения (3.27) получим

₂ = ₁ctg² или 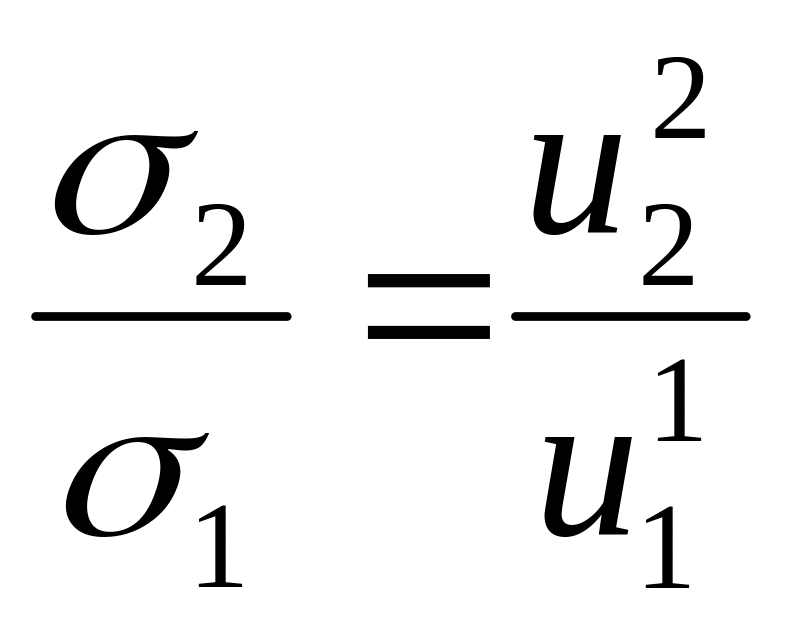(3.29)

Рис. 3.11. Внешние и внутренние силы в ячеях сети.	Рис. 3.12. Переход от непре­рыв­ной модели сети к дискретной

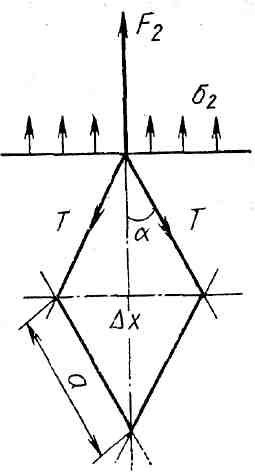
Для определения величины натяжения нитей рассмотрим схему, изображенную на рис. 3.12. Очевидно, что F₂ = ₂x= ₂asin. Кроме того, F₂ = 2Tcos. Приравнивая правые части, получим T = ₂ a tg. (3.30)

Рассмотрение аналогичной схемы для горизонтальных сил Ft дает

T = ₁ a ctg.. (3.31)

Таким образом, мы перешли к натяжению в отдельных нитях как функции от распределенной по сети внешней нагрузки, величины шага ячеи и посадки, т. е. перешли от непрерывной модели сети к дис­кретной.

Соотношение сил, растягивающих сеть. Если сеть длиной L и вы­сотой Н растягивается по кромкам вертикальными P_y и горизонталь­ными Р_x нагрузками, то, поскольку Р_y = _L, Р_x = _H, соотноше­ние между ними будет

(3.32)

Рис 3.13 Деформация боковых участков сети, нагруженной вертикальными силами

Взаимозависимость вертикальных и горизонтальных нагрузок учитывают при выборе коэффициентов посадки. Так, например, при и_X= 0,5 в соответствии с выра­жением (3.29) имеем _y = 3_x, a при и_X= 0,87 вертикальная нагрузка снижается до  _y = l/3_x. Отче­том этого иногда применяют посадку жаберных сетей и кошелько­вых неводов с большим и_X. Для тралов же большие и_х нежелательны, поскольку это вызывает повыше­ние стяги­ва­ющих усилий по пе­риметру трала и снижение его рас­крытия.

В сети, нагруженной верти­каль­ными силами, возникает де­форма­ция ее боковых участков. Из рис. 3.13 видно, что левее линии ABC нагружены все четыре нити, вы­ходящие из каждого узла. На участках, ограни­чиваемых линия­ми ABD и СВЕ, нагружены лишь три нити каждого узла, а в узлах, расположенных на участке, огра­ничиваемом линией DBE, нагру­жены только две нити в каждом узле. Вследствие этого узлы сети, расположенные правее линии ABC, стремятся сдвинуться влево. Аналогичное явление имеет место на левом боковом участке сети. Если же приложить к сети не вертикальные, а горизонтальные на­грузки, то выгибаться будут ее верхняя и нижняя кромки. По этой же причине (несимметричные нагрузки в узлах) расходятся края отверстия внутри сети при ее порывах.

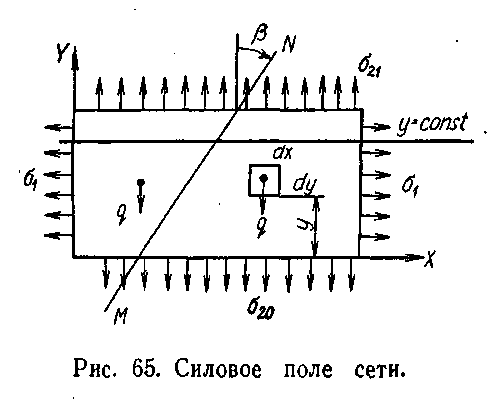
Сеть под действием параллельных сил, понятие о силовом поле сети. Пусть на прямоугольную сеть, рассмотренную ранее, помимо растягивающих сил, действуют дополнительные внешние силы q_y равномерно распределенные по ее площади (рис. 3.14). Положим» что форма всех ячей сети сохраняется одинаковой, т. е. и_х = const, и_y = const. Выделим из сети бесконечно малый элемент со сторонами dx и dy, нижняя кромка которого имеет ординату у, и рассмотрим условия его равновесия (рис. 3.15). С учетом размеров элемента внешняя сила, приходящаяся на его площадь, будет qdxdy.

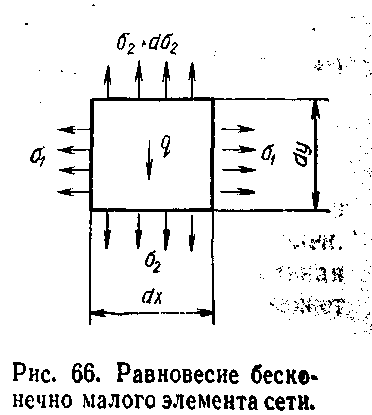
Рис 3.14 Силовое поле сети	Рис 3.15 Равновесие бесконечно малого элемента сети

Тогда, проектируя все силы на ось Y, получим (₂ + d₂)dx – ₂dx – qdxdy = 0 или d₂ – qdy = 0, откуда после интегрирования и оп­ределения произвольной постоянной

 ₂ = qy+  _2О (3.33)

^{С учетом выражения (3.28) получим}

 ₁ = (qy+  _2О )tg². 3.34)

На любой горизонтальной линии у = const величины _ и ₂ не­изменны. Но вдоль других линий сети, например вдоль линии MN (см. рис. 3.14), характеризуемой углом , они изменяются. Такую идеа­лизированную сеть можно рассматривать как силовое поле ₁ или  ₂. Линии уровня у = const совпадают здесь с горизонтальными диаго­нальными линиями ячей сети, а градиент этого поля совпадает с вертикальными диагональными линиями. Градиенты поля с учетом выражений (3.33) и (3.34) будут

(3.35)

(3.36)

Изменение  ₁ и ₂ вдоль любой линии MN найдем с учетом того, что линейный элемент ds вдоль линии MN будет ds == dy/cos, поэто­му градиенты  ₂ и  ₁ вдоль линии MN составят

(3.37)

(3.38)

Силовое поле сети может представлять собой поля нескольких сил, которые связаны между собой. Так, помимо рассмотренных сил ₁ и ₂ имеет место поле сил натяжения нитей N, внешних сил q и скалярное поле коэффициента посадки и(х, у) — факторов, которые в общем случае могут быть переменными по поверхности сети.

Рис 3.16 Обеспечение требуемой формы сети	Рис 3.17 Бесконечно малый элемент на кромке сети

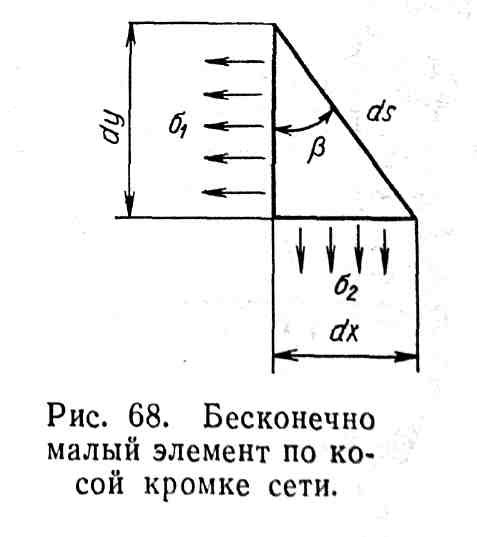
Обеспечение требуемой формы сети. Пусть задана требуемая форма сети ABCD, показанная на рис. 3.16. Чтобы эта форма была обеспечена, необходимо приложить по кромке сети ВС соответствующие силы (_x)_S и (_y)_S. Для их определения выделим малый участок сети, пред­ставляющий собой прямоугольный треугольник, гипотенуза кото­рого совпадает с косой кромкой сети ВС (рис. 3.17). Очевидно, что _y dx= (_y)_Sds,

откуда (3.39)

аналогично _y dx= (_y)_Sds

(3.40)

Таким образом, приложение сил (_х)_S и (_y)_S по кромке ВС на­ряду с приложением сил _x по кромке AD и _y по кромкам АВ и АС обеспечивает требуемую фор­му АВСД нагруженной сети.

Статика плоской рыболовной сети. Если к горизонтальным кромкам плоской прямоугольной сети приложены вертикальные растягивающие нагрузки Р_В (рис. 16), то для того чтобы сеть сохранила форму прямоугольника, к ее вертикальным кромкам должны быть приложены соответствующие по величине горизонтальные растягивающие усилия Р_г. Связь между вертикальными и горизонтальными усилиями имеет вид

(3.41)

Растягивающая нагрузка, приходящаяся на единицу длины кромки сети, называется напряжением и обозначается

₁=Р_Г/h= ₁= Р_B/1. (3.42)

Напряжения связаны между собой выражением

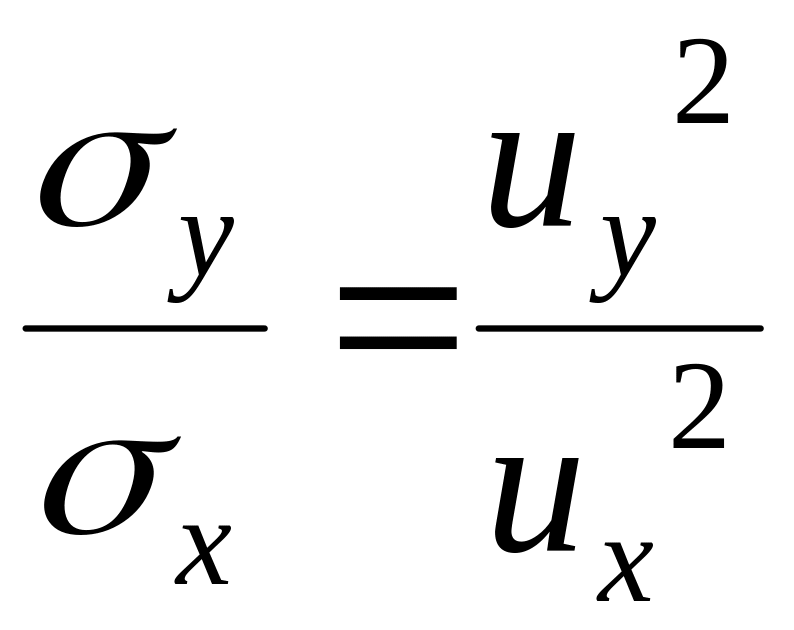(3.42.а)

Под действием нагрузок, приложенных к кромкам сети, в ее нитях возникают натяжения Г, вычисляемые по формулам:

T=_y·a·tga, (3.43)

T = _x·a·ctga. (3.44)

Если помимо нагрузок по горизонтальным и вертикальным кромкам сети в ее плоскости действуют равномерно распределенные силы q (сила тяжести или гидродинамического сопротивления), то напряжения в каждой точке сети определяются по фор­мулам:

₂=qy+₂₀ (3.45)

₁=(qy+₂₀)tg²a. (3.46)

Такая сеть находится в силовом поле ₂ и ₁. Линии уровня у = const совпадают в рассматриваемом случае с горизонтальными диагоналями ячей, а градиент поля — с вертикальными диагоналями (х=const).

И

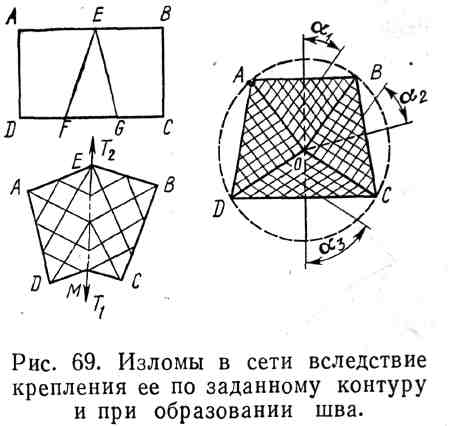
Рис 3.18 Изломы в сети вследствие крепления её по заданному контуру и при образовании шва

зломы в сети и концентрации напряжений. Выше форма сети зада­валась, а затем определялись усилия, которые обеспечивают сохране­ние этой формы. При обратной постановке задачи, когда задают усилия по кромкам сети и ищут ее форму, решения значительно усложняют­ся. Кроме того, при произвольном задании усилий по кромкам сети весьма вероятно появление в ней деформаций типа излома, вызываю­щих концентрацию напряжений по определенным направлениям и, как следствие этого, снижение прочности сети.

В качестве примера изломов в сети рассмотрим рис. 3.18. Посажен­ная на подборы сеть ABCD первоначально имела прямоугольную фор­му с равным количеством ячей по всем сторонам. После закрепления сети к обручу точки ABCD лежат на окружности с центром О. Коэффициенты посадки по кромкам сети стали соответственно

u_AB=sin₁

u_DC=sin₃

u_AD= u_BC=cos(₁+_)/2 (3.47)

Последнее равенство вытекает из того, что 2(₁ + 2₂ + ₃) = 360° или  ₂ = 90 - (₁ + ₃)/2. Из рис. 3.18 видно, что поле такой сети составлено как бы из четырех отдельных регулярных силовых полей. Их границы — линии излома, на которые ложится дополнительная нагрузка, следствием чего именно вдоль них прежде всего может иметь место обрыв нитей.

Рассмотрим еще один пример. Пусть из прямоугольной сети ABCD вырезали кусок FEG и затем сеть соединили по кромкам EF и GF.

Кромка ЕМ является линией излома, и вдоль нее возникает дополнительная нагрузка Т. Однако структура этой кромки такова, что она этой нагрузки воспринимать не может. Вот почему для подкрепления подобных кромок необходимо ставить топенанты и пожилины.

Литература: [1], стр. 75-92.

Вопросы для самоконтроля

1. Какую форму принимает сетное полотно, посаженое с разными коэффициентами по верхней и нижней подборе?

2. Какова зависимость между горизонтальным и вертикальным посадочными коэффициентами?

3. Как определяется натяжение в сети при её линейной деформации?