Вопросы для самоконтроля

1.Опишите порядок построения формы цепной линии.

2.Опишите порядок построения формы сети нагруженной силой сопротивления.

3.Опишите порядок построения формы уреза, буксируемого по грунту.

Литература: [1], стр. 69-75.

Раздел 3. Механика сетей

3.1 Геометрия и статика рыболовных сетей

3.1.1. Общие свойства рыболовных сетей

Непрерывная и дискретная модели рыболовной сети. Рыболовные сети являются основным конструкционным материалом большинства рыболовных орудий. Помимо промышленного рыболовства, сетные оболочки применяются и в других отраслях народного хозяйства (тканевые оболочки, вантовые сетки, резинокордные оболочки и др.). Специфика расчета сетных оболочек орудий лова обусловлена преж­де всего следующими двумя особенностями: взаимная обусловлен­ность внешних гидродинамических сил формой и структурой оболоч­ки (раскрытие ячей); каркас сетной оболочки, состоящей из системы канатов, не является жестким и также может изменять свою форму под действием приложенных к нему сил.

Эти особенности усложняют расчет сетных оболочек, и до настоя­щего времени конечные результаты получены лишь для простейших задач проектирования. Основные результаты содержатся в работах Ф. И. Баранова, Н. Н. Андреева, А. И. Зонова, Ю. А. Изнанкина.

Рыболовная сеть без надлежащего закрепления и нагружения определенной формы не имеет и приобретает ее, лишь будучи соот­ветствующим образом закрепленной и нагруженной внешними силами. При расчете сетной оболочки можно пользоваться непрерывной или дискретной моделью.

Рис 3.1 Характеристики ячеи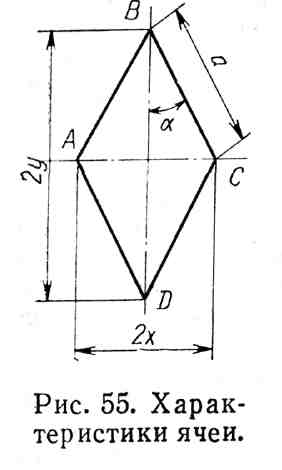

Непрерывная (континуальная) модель сетной оболочки — бес­конечно тонкая, идеально гибкая, непрерывная оболочка, поверх­ность которой образо­вана двумя семействами бесконечно большого числа пересекающихся нитей. Внешние силы уравновешиваются толь­ко натяжениями растянутых нитей. Узлы сети фиксированы и разбивают ее на одинаковые структурные элементы. Таким образом, непрерыв­ная модель отличается от реальной сети бесконечно малы­ми разме­рами ячей, отсутствием жесткости нитей, отсут­ствием отклонений шага ячеи от номинального. Проведенные исследования показали, что при таких допущениях ошибка в расчетных параметрах формы обычных сетей во многих практических случаях не превышает 3 — 5%. Однако в расчетах крупноячейных сетей предпочтительнее может ока­заться дискретная модель сети. Эта модель пред­ставляет собой конструкцию из шарнирно-соединенных стержней. Каждая сетная нить—сторона ячеи — рассматривается как стержень. Непрерыв­ная модель в настоящее время является более разработанной и используется чаще.

Расчет сетной части рыболовного орудия мо­жет считаться законченным, когда определены ее геометрические размеры, раскрой сетей, ассортимент делей, напряжения в любой точке поверхности сети, оснастка подбор и их натяжение. Помимо прочего, сложность таких расчетов вызыва­ется многовариант­ностью режимов внешнего нагружения орудий лова на различных этапах процесса лова и при различных условиях промысла. Изменения внешних нагрузок ведут к изменению расчетной формы сетей, образованию концентрации напряжений в ее отдельных местах. Поэтому расчеты для различных этапов эксплу­атации данного рыболовного орудия должны завершаться провер­кой общей и местной прочности его сетной части.

Наряду с обычными сетями с ячеей ромбической формы некоторое распространение получают сети с ячеей другой формы, и в частности, с ячеей в форме шестиугольника.

Свойства ячеи. Если ячея (рис. 3.1) расправлена на плоскости таким образом, что расстояния а между ее узлами одинаковы и нитки не имеют складок и разрывов, то справедливы соотношения и_х = х/а = sin, u_Y = y/a = cos, которые называют коэффициентами посадки. Нетрудно видеть, что в этом случае и_Х²+ и_Y² =1 (3.1)

Таким образом, коэффициенты посадки и_X и и_Y взаимозависимы и однозначно определяют форму ячеи при условии, что сеть не имеет складок и разрывов. Форма сети определяется формой отдельной ячеи. Последняя же зависит от посадки сети на подборы, которая определяется в простейшем случае величиной коэффициента

(3.2)

где l — длина подборы; s — длина сети в жгуте.

Если посадка сети вдоль подборы непрерывно изменяется, то на некотором отрезке подборы СС₁=l среднее значение коэффици­ента посадки будет u_CP=l /s, где s — длина сети в жгуте, по­саженной на данный отрезок подборы. Приближая точку С₁ к точке С, получим в пределе истинное значение коэффициента посадки в точ­ке С в виде (3.3)

Линейные деформации ячеи. При линейных деформациях сети форма отдельной ячеи изменяется, в то время как форма ее диагональ­ных линий АС и BD (см. рис. 55) остается неизменной. Из рис. 55 следует

х = a sin , у = a cos . (3.4)

При малой линейной деформации ячеи величины х и у получают приращения dx = acosda, dy = –a sinda, откуда

(3.5)

или (3.6)

Следовательно,

(3.7)

(3.8)

Таким образом, деформация ячеи вдоль оси х вызывает деформа­цию ее по оси у, и наоборот. Величины этих деформаций зависят от соотношения коэффициен­тов посадки.

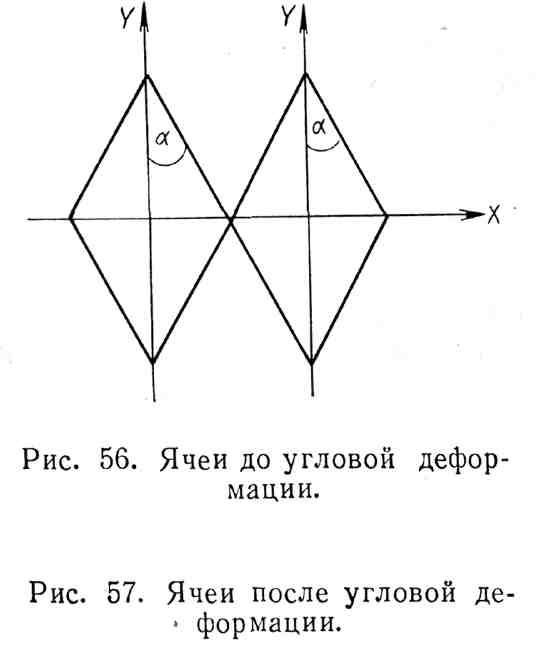
Угловые деформации сети. При угловых деформациях сети диаго­нальные линии отдельных ячей изменяют свое направление. Рас­смотрим две ячеи, показанные на рис. 3.2.

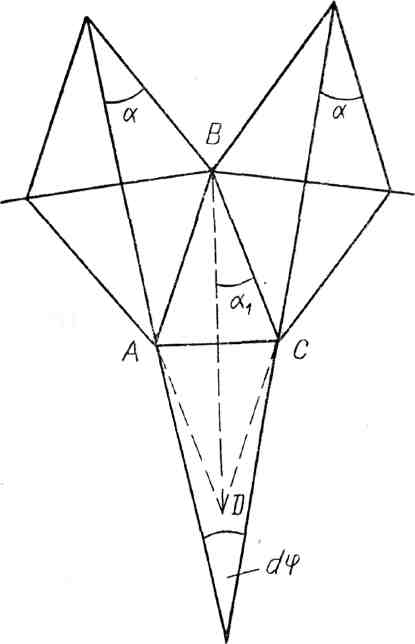
Допустим, что в первоначальном положении горизонтальные диагонали этих ячей совпадали, а вертикальные были между собой параллельны. После угловой деформации ячеи будут иметь вид, по­казанный на рис.3.3. Их форма остается неизменной, но связанная с ними ячея ABCD изменяет свою первоначальную форму, поскольку ₁<. Таким образом, угловая деформация в одном ряду ячей при­водит к изменению формы ячей в последующих рядах.

Коэффициент использования сетного полотна. Рассмотрим прямо­угольную сеть с постоянным шагом ячеи а. Число ячей по длине сети n, число ячей по ее высоте т. Длина сети в жгуте L₀, а высота Н₀. Размеры сети после посадки L и Н будут L= L₀ •и_x (3.9) Н= Н₀ •и_y (3.10)

Рис 3.2 Рис 3.3

Площадь сети в посадке F = LH, а фиктивная площадь ее L_ф — = L₀H₀. Учитывая, что L₀ = 2ап, а H = 2am, имеем

F = 4a²mn sin  cos  (3.11)

и F_Ф = 4a²mn (3.12)

отношение (3.13)

называют коэффициентом использования сетного полотна. С учетом выражений (3.11) и (3.12) получаем  = и_Xи_Y. (3.14)

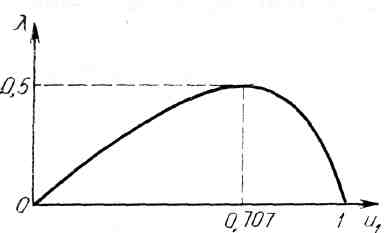
Зависимость  = f(и_X) показана на рис. 3.4.

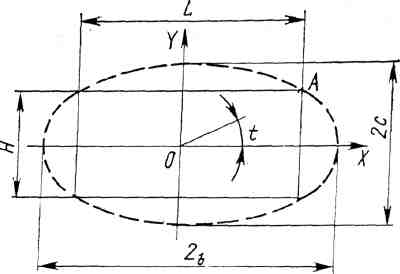
Линейные деформации прямоугольной сети. Чтобы исследовать формоизменяемость прямоугольной сети (рис. 3.5) при различных вариантах ее посадки, рассмотрим траекторию точки А. Размеры сети обозначим как

L = 2па sin , H = 2ma cos . (3.15)

Соответственно координаты точки А будут

x = nasin, у = та cos. (3.16)

Система уравнений (3.16) аналогична параметрическим уравне­ниям эллипса

х = b cos t, y = с sin t,

где b и с — полуоси эллипса; t — текущий угол радиуса вектора ОА с осью X,

Таким образом, очевидно, что при изменении формы сети точка А движется по эллипсу с полуосями b = an и с — am. В частном случае, когда п = т, эллипс становится окружностью. Следова­тельно, при всех вариантах посадки сеть является прямоугольником, вписанным в соответствующий эллипс с полуосями am и an.

Рис. 3.4. Зависимость коэффици­ента использования сетного по­лотна X от посадки сети.	Рис. 3.5. Формоизменяемость пря­моугольной сети.

Из системы уравнений (3.16) получаем

dx = па cos ada,, dy = — та sin ada, (3.17)

откуда следует

(3.18)

(3.19)

Выражения (3.18) и (3.19) отличаются от выражений (3.7) и (3.8) для деформаций ячеи тем, что в них входят соотношения ко­личества ячей т и п по высоте и длине сети.

Форма ячеи натянутой сети определяется поса­дочными коэффициентами. Посадочным коэффи­циентом называют соотношение длины каната L, на которую са­жается сеть, и длины сажаемой сетной кромки в жгуте L0 (рис. 3.6). uX=L/L0 Аналогично по боковой кромке: uY=H/H0 Посадочные коэффициенты связаны между собой зависимостью: uX2+ uY2=1

Рис. 3.6

При линейных деформациях прямоугольной сети связь между приращениями высоты и длины сети, вызванными линейными деформациями, имеет вид.

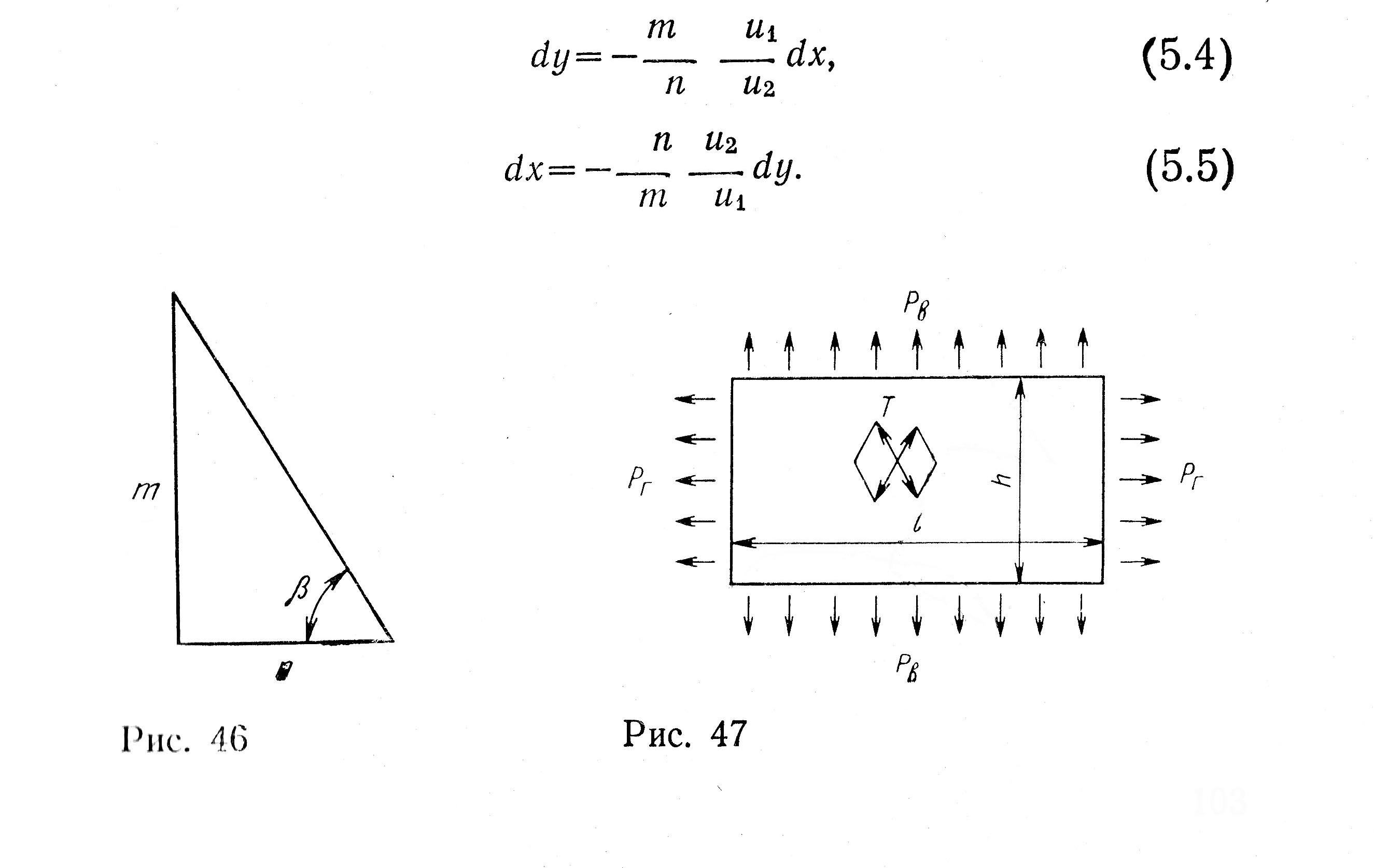
Рис. 3.7 Рис. 3.8

Коэффициент посадки и_Х соответствующий заданной углом  форме клиновидной сети (рис. 3.7), рассчитывается по формуле

(3.20)

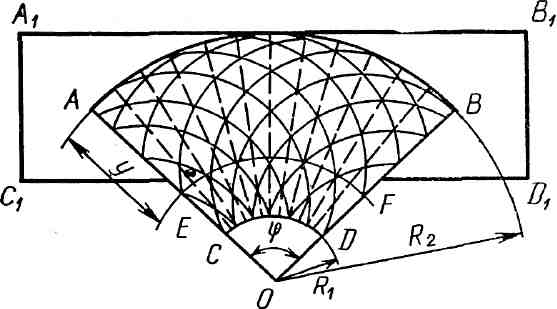
Некоторые свойства прямоугольной сети при угловых деформа­циях. Если прямоугольная сеть посажена на подборы таким обра­зом, что посадочный коэффициент по верхней подборе u_X2 отличается от посадочного коэффициента по нижней подборе и_X1 то на плоскости такая сеть (рис. 3.9) вместо прямоугольной формы A₁B₁C₁D₁ примет форму части кругового кольца ABCD. Диагонали ячей сетного полотна взаимно перпендикулярны. В случае, когда сеть приняла форму кругового кольца, одно семейство диагоналей представляет собой концентрические окружности, а другое — пучок прямых, проходящих через начало координат. Сказанное позволяет установить высоту сети, например, кошелькового невода после кошелькования.

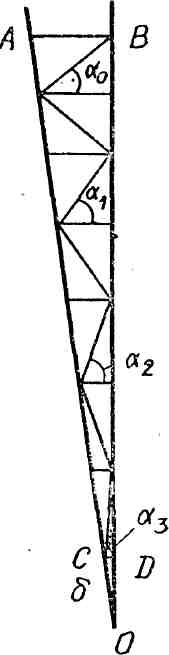
Рассмотрим какой-нибудь один ряд ячей сетного полотна (рис 3.10) Здесь высота сети Н будет Н = О А —ОС, а длина подбор АВ и CD выразится как АВ = ОА, CD = ОС. Поэтому Н = (АВ — CD)/. Кроме того, АВ = аи_X2 и CD = а и_X1 где и_X2 и и_X1 – коэффициенты посадки сети по верхней и нижней подборам соответственно.

Поэтому

Чтобы определить  через заданные величины коэффициентов по­садки по подборам и_X2 и и_X1 и количество ячей по высоте сети m, заме­тим, что из рис. 3.10 можно найти следующие соотношения: ₁ =  ₀ + 2 ,  ₂ =  ₀ + 4 , ...,  _т =  ₀ + 2m или а_m – а₀ = 2m .

Рис. 3.9. Форма сети с разными посадочными коэффициентами по верхней и нижней подборам.	Рис. 3.10. Вертикальный ряд ячей се­ти в случае разных посадочных ко­эффициентов по подборам.

Учитывая, что и_X2 = cos₀, и_X1 = cos_m или ₀ = arccos и_X2=  — arcsin и_X2 , _m = arccos и_X1=  — arcsin и_X1 , получим _т — ₀ =

= arcsin и_X2 — arcsin и_X1 = 2m , откуда . Подставляя выражение  в выражение (3.20), получим

где H_O — высота сети в жгуте.

Нетрудно видеть (см, рис, 3,9), что

H = R₂ — R₁ (3.22]

где

(3.23)

Коэффициенты посадки для любой точки сети можно найти, если учеcть, что при Ri = const u_i = const. Как видно из рис. 3.9, коэффициент посадки для ряда ячей,- определяемого некоторым Ri, будет

Соответствующий переменный коэффициент посадки по высоте сети при Ri определится из основного уравнения связи коэффициен­тов посадки. Необходимую величину можно найти, например, по формуле

(3.25)

Если соединить между собой боковые кромки такой сети, то она примет форму кругового конуса.