7 Классы грамматик. Понятие контекстно-свободная граматика (cfg).

Иерархия Хомского — классификация формальных языков и формальных грамматик, согласно которой они делятся на 4 типа по их условной сложности. Для отнесения грамматики к тому или иному типу необходимо соответствие всех её правил (продукций) некоторым схемам. По иерархии Хомского, грамматики делятся на 4 типа, каждый последующий является более ограниченным подмножеством предыдущего (но и легче поддающимся анализу): тип 0. неограниченные грамматики — возможны любые правила; тип 1. контекстно-зависимые грамматики — левая часть может содержать один нетерминал, окруженный «контекстом»; сам нетерминал заменяется непустой последовательностью символов в правой части; тип 2. контекстно-свободные грамматики — левая часть состоит из одного нетерминала; тип 3. регулярные грамматики — более простые, эквивалентны конечным автоматам.

Контекстно-свободная грамматика— частный случай формальной грамматики (тип 2 по иерархии Хомского), у которой левые части всех продукций являются одиночными нетерминалами. Смысл термина «контекстно-свободная» заключается в том, что возможность применить продукцию к нетерминалу, в отличие от общего случая неограниченной грамматики Хомского, не зависит от контекста этого нетерминала. Например: Слово с переворотом (Палиндром). Задаётся формулой ; Терминалы: буквы алфавита Σ; Нетерминал: S; Продукции: ; Начальный нетерминал — S.

8 Конечные автоматы и регулярные выражения.

Конечный автомат — это пятёрка M = < K, Σ, , s, F >, гдеK – конечный набор состояний, Σ — конечный алфавит, s – начальное состояние, F – множество конечных состояний, — функция перехода, функция из K x Σ. Если язык регулярен, то он принадлежит замыканию класса, содержащего однобуквенные языки и 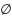, относительно , конкатенации и звездочки Клини. Язык регулярен тогда и только тогда, когда он распознается конечным автоматом. Пусть имеется конечный автомат M = <K, Σ, ∆, s, F>. Построим регулярное выражение R такое, что L(R) = L(M). Представим L(M) в виде объединения конечного числа более простых языков. Пусть K = {q1,…, qn}, и s = q1. Для i, j = 1,…, n и k = 0,…, n будем определять R(i, j, k) как множество всех слов Σ∗, которые могут перевести M из состояния qi в состояние qj без прохождения через промежуточное состояние с номером k + 1 или больше (конечные точки qi и qj могут иметь номера большие чем k) . Когда k = n, мы получаем, что R(i, j, n) = {w ∈ Σ∗|<q, w> |-∗M <qj, e>}. Следовательно L(M) = {R(1, j, n)|qj ∈ F}. Значит, если все множества R(i, j, k) окажутся регулярными, то регулярным будет и L(M). То, что каждое R(i, j, k) -регулярно, доказывается индукцией по k. Для k = 0 возможны два случая. Если i j, то R(i, j, 0) = {a ∈ Σ ∪ {e}|<qi, a, qj> ∈ ∆}. Если i = j, то R(i, j, 0) = {e}∪{a ∈ Σ∪{e}|<qi, a, qj> ∈ ∆}. Каждое из этих множеств является конечным, а следовательно регулярным. Теперь предположим, что для всех i, j уже доказано, что R(i, j, k − 1) регулярные языки. Тогда R(i, j, k) = R(i, j, k − 1) ∪ R(i, k, k − 1)R(k, k, k − 1)∗R(k, j, k − 1). Данное равенство означает, что при движении из qi в qj без прохождения через состояния с номерами, большими чем k, у автомата M есть два варианта: 1 . идти из qi в qj без прохождения через состояния с номерами, большими чем k − 1; 2. идти из qi в qk , затем из qk в qk 0 или более раз, затем идти из qk в qj ; каждый раз без прохождения через промежуточные состояния с номерами, большими чем k − 1. Таким образом язык R(i, j, k) регулярен при любых i, j, k. Значит, регулярным является и язык L(M).