Шпоры по дискре (2 семестр)
.doc
|
32. (1 из 1) Подгруппы конечных циклических групп. |
33. (1 из 1) Фактор-группы циклических групп. |
|
Пусть
Доказательство: Пусть
Покажем,
что
Случай
|
Любая фактор группа циклической группы - циклическая. Доказательство: Пусть Покажем,
что
Пусть
|
|
34. (1 из 2) Порядок элемента группы и прямые произведения циклических групп. |
34. (2 из 2) Порядок элемента группы и прямые произведения циклических групп. |
|
Пусть G – группа. Тогда
минимальное нат. число k.
Такое, что
5º.
Пусть
Тогда: 1) G
– циклическая группа
2) Если
НОД( Доказательство: G
– циклическая группа
Но
Тогда
Но
Кроме
того,
Таким
образом
Следствие: Пусть
G – циклическая группа.
Тогда
|
Доказательство: По свойству 5º группа
H – циклическая. Кроме
того,
|
|
35. (1 из 2) Группы подстановок. |
35. (2 из 2) Группы подстановок. |
|
Определение Подстановка
на множестве М – любое биективное
отображение.
Утв:
Элементы
Пример: 1) n=3
2
|
Утв:
Пусть
Доказательство: Пусть
|
|
36. (1 из 1) Теорема Кели. |
37. (1 из 1) Разложение подстановок в произведение независимых циклов. |
|
Теорема Пусть
G – группа,
Доказательство:
( Покажем,
что
Пусть
Докажем
теперь, что
Рассмотрим
|
Пример:
Опр: а)
б)
Подстановка, состоящая из неодного
единичного цикла, называется циклом
[ в)
циклы
Опр:
Подстановки
Пример:
|
|
38. (1 из 1) Цикловая структура подстановки и ее порядок. |
39. (1 из 1) Представление подстановок в виде произведения транспозиций. Четные подстановки. |
|
Опр:
Пусть
Пример:
Проверка
соотношения
Св-во3:
Пусть
а) g
– цикл длины k. Тогда
б) g
имеет циклическую структуру
(т.е ◄а)
б)
Пусть
Тогда
|
Опр:
Пусть Утв:
Любая
◄Представим
g в виде произв. Независ.
циклов, т.е. Опр:
подстановка
|
|
40. (1 из 1) Критерий четности подстановки. Знакопеременная группа. |
41. (1 из 1) Системы образующих симметрической группы. |
|
Опр:
Св-ва:
Утв:
Пусть
◄]
Но
|
Теорема:
а) б) в) г) ◄а) доказано ранее б) (i,j)=(1,1)(1,j)(1,i) в) (1,i)=(1,2)…(i-1,i)(i-2,i-1)..(1,2) г)
|
|
42. (1 из 1) Системы образующих знакопеременной группы. |
43. (1 из 1) Подкольца и идеалы кольца. Критерий подкольца. Полкольцо порожденное множеством. |
|
Теорема2:
◄ а) i,j,k,l – все различны. (i,j)(k,l)=(i,j,k)(l,k,i) б) i,j,k – различны 1) l=i : (i,j)(k,l)=(i,j)(k,i)=(i,j,k) 2) l=j : (i,j)(k,l)=(i,j)(k,j)=(i,k,j) в)
(i,j)(i,j)=е.
Но
|
Опр: K(+,*) – кольцо. K1(+,*)<K(+,*)- подкольцо, если а) б) K1 – кольцо. Критерий подкольца Опр:
Подкольцо Обозначается Св-во1:
Св-во1:
Опр:
Пусть
Опр:
(K-
кольцо главных идеалов, если Утв.: Гомоморфный образ кольца (поля) есть кольцо (поле) |
|
44. (1 из 1) Кольцо вычетов по модулю натурального числа. |
45. (1 из 1) Кольцо многочленов над полем. Деление с остатком. |
|
Def: Если на множестве Z задано отношение x Ξ y(mod m)m l (x-y), (x,y,m Є Z) и если заданы операции «+» и «*», т.ч. {k}m+{l}m={k+l}m {k}m*{l}m={k*l}m , где {k}m – класс вычетов по m, {k}m=k+mZ={r+mk : k Є Z}, то Zm(+,*) называется кольцом классов вычетов по модулю натурального числа m. x Ξ y(mod m) означает, что при делении на m x и y дают одинаковые остатки.
|
Кольцо многочленов над полем Пусть
P – поле. Послед-ть
На P[x] рассмотрим опреации: 1) 2)
Легко видеть, что P[x](+,*) является коммутат. кольцом с единицей.
Замечание. Пусть x=(0,1,0,…) x2=(0,0,1,0,…) x3=(0,0,0,1,0,…) ……. x2=(0,…,0,1,0,…) Тогда
Опр: степенью многочлена
Опр: 1) 2) Замечание: если P-поле, то деление с остатком имеет место (т.е. q(x) и r(x) однозначно определены)
|
|
46. (1 из 1) НОД многочленов. |
47. (1 из 1) Алгоритм Евклида вычисления НОД. |
|
Опр:
а)
б)
если
|
Утв: 1)
2)
Пусть d(x)
= НОД(a(x),b(x)),
тогда
множество всех НОД а(х) и b(x)
совпадает с
Заметим, что если d(x) = НОД(a(x),b(x)), то cd(x)=НОД(a(x),b(x)), с Є Р Если
Пусть
Т.к.
имеет место посл-ть строгих неравенств
относительно степеней многочленов,
то
|
|
48. (1 из 1) Расширенный алгоритм Евлида. |
49. (1 из 1) Гомоморфизмы колец. Теорема об эпиморфизме колец. |
|
Утв:
◄Док-во
сводится к рассмотрению при n=2.
См док-во пред Утв. По алгоритму
Евклида:
|
Гомоморфизм колец Опр:
Пусть
Утв:
[аналогично для групп] Утв(Теорема об эпиморфизме колец): Пусть
1)
2)
(
(только если I - идеал)
[аналогично для групп]
|

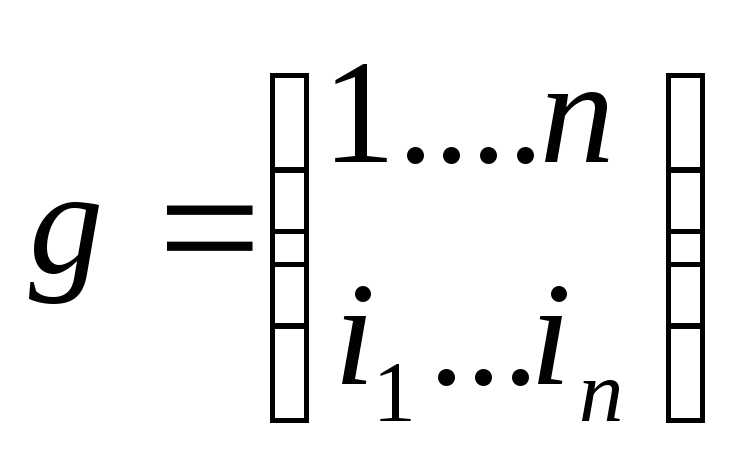 ,
где
,
где
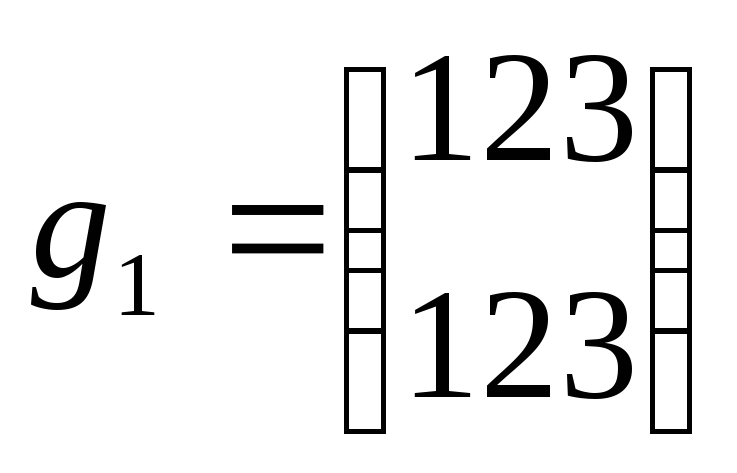 -
тождественная подстановка
-
тождественная подстановка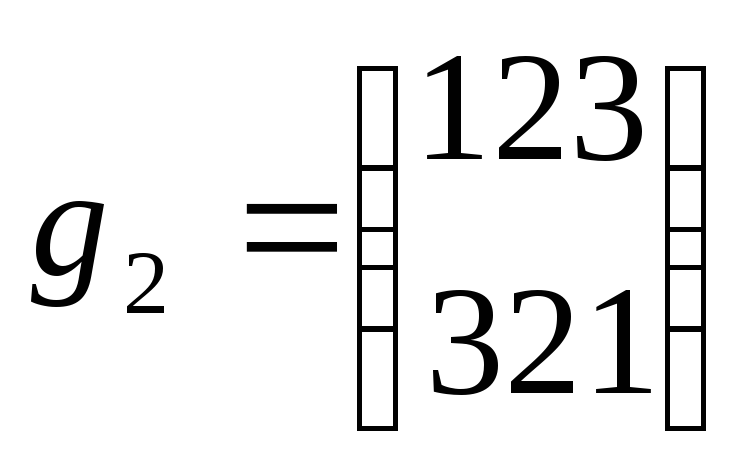
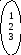
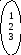
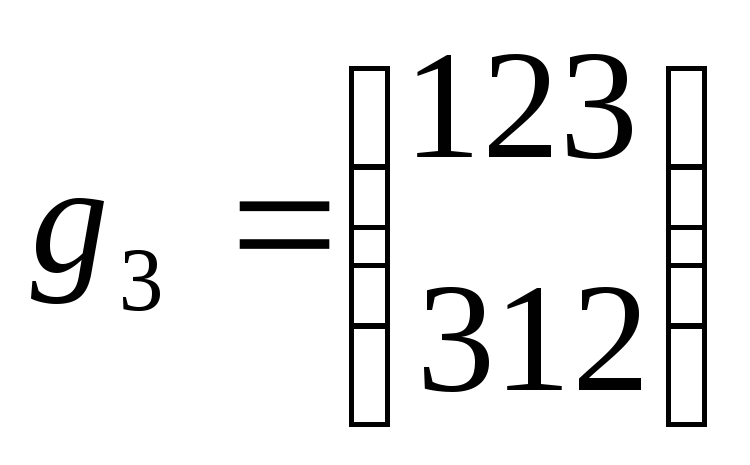 …
… 
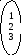








 )
Умножение подстановок
)
Умножение подстановок












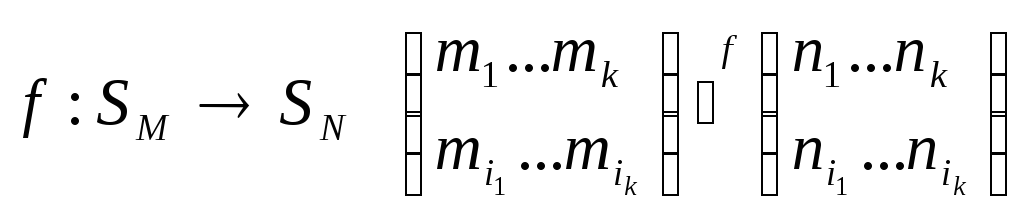 .
#
.
#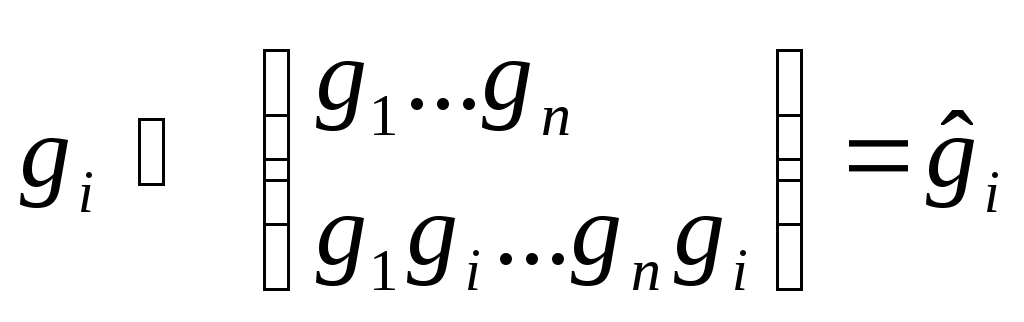 G
– группа
G
– группа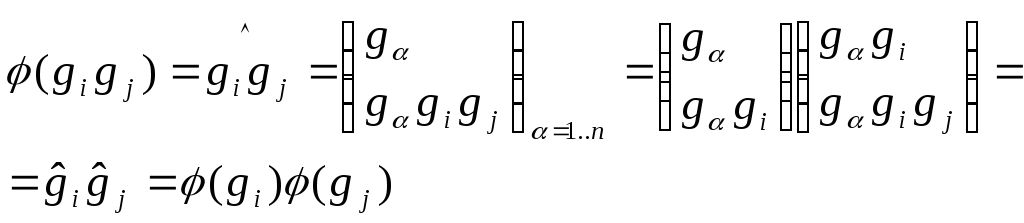
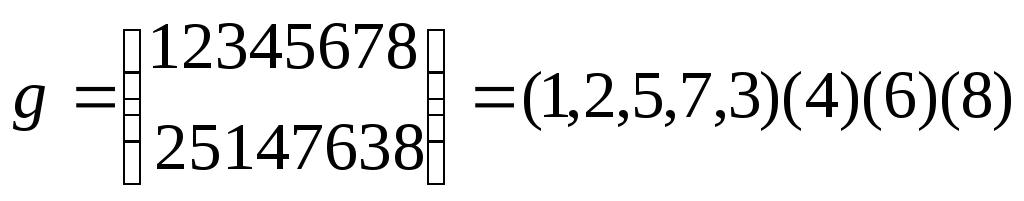
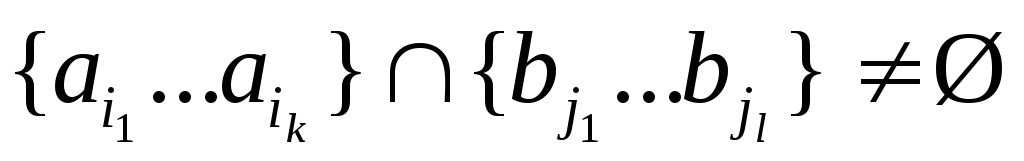
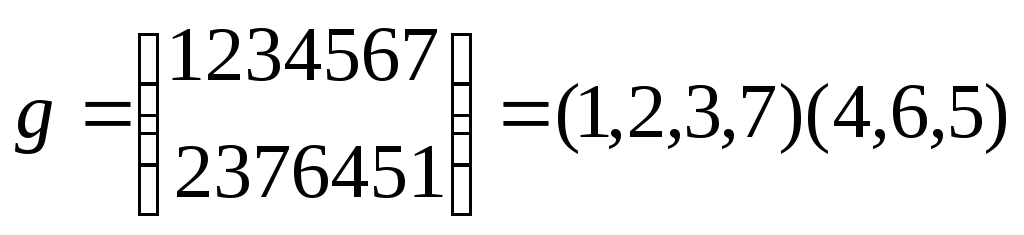
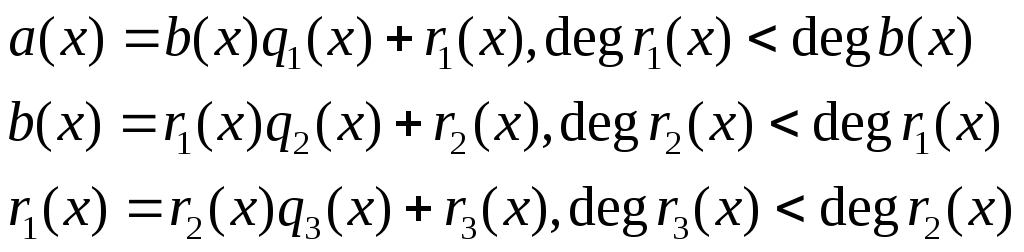
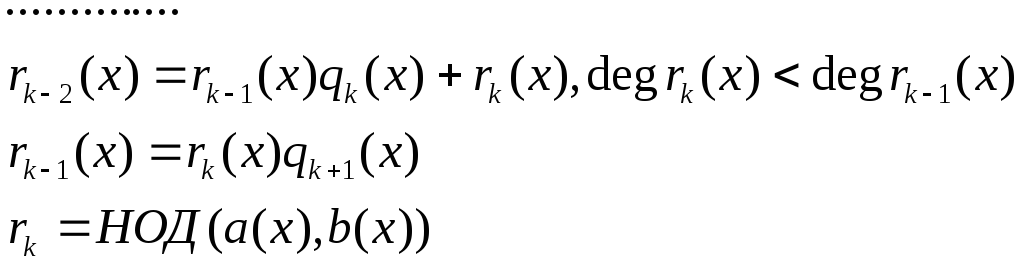
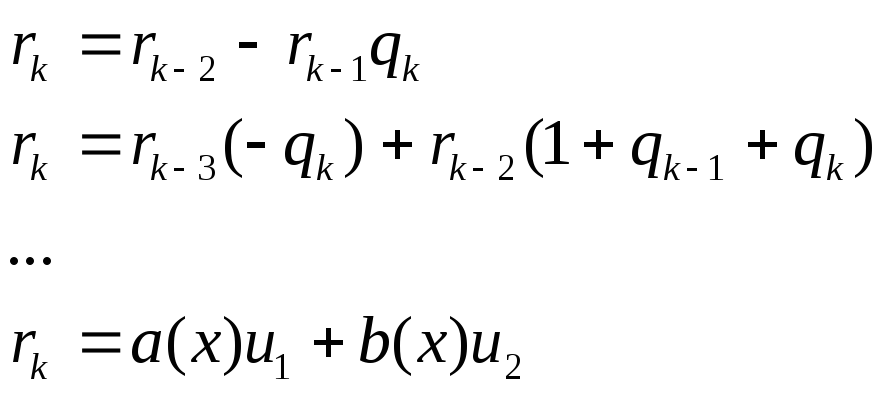 ►
►


 K
K