7.Приращение аргумента и приращение функции, их геометрическая иллюстрация. Два равносильных определения функции, непрерывной в точке. Непрерывность основных элементарных функций.

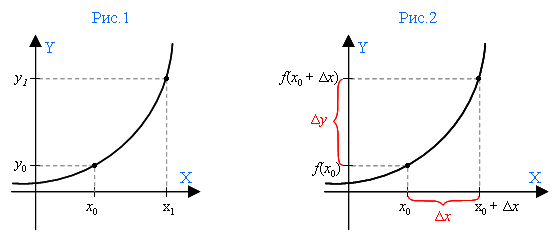
На оси Х – две точки: x₀ и x₁ (рис.1). Если от x₁ отнимем x₀, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x₀. Эта разность между двумя соседними точками оси X и называется приращением аргумента.

Точки x₀ и x₁ образуют на оси Y соответствующие им точки у₀ и у₁. Если от  у₁ отнять у₀, то мы получим приращение функции.

Итак, в функции y = f(x) относительно определенных точек x₀ и x₁: разность x₁ – x₀ называется приращением аргумента, а разность у₁ – у₀ называется приращением функции.

Но у₀ и у₁ – зависимые переменные (зависимые от значений х). То есть их правильно записывать так: f(x₀) и f(x₁). Следовательно, приращение функции – это разность f(x₁) – f(x₀).

Приращение обозначается греческой буквой Δ (дельта):

Δx = x₁ – x₀;

Δy (или Δ f) = f(x₁) – f(x₀).

Можно сказать и иначе: если к x₀ прибавить величину приращения Δx, то мы получим точку x₁.  То есть x₁ = x₀ + Δx (рис.2).  Тогда точку f(x₁), отмеченную на первом рисунке как у₁, тоже можно обозначить иначе: f(x₀ + Δx).

Формула приращения функции:

Δy = f(x0 + Δx) – f(x0) или Δf = f(x0 + Δx) – f(x0)

Пусть   и  .

Функция   непрерывна в точке  , если для любого   существует   такое, что для любого

Функция   непрерывна на множестве  , если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция   класса   и пишут:   или, подробнее,  .

[Править]Комментарии

• Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция   непрерывна в точке  , предельной для множества  , если   имеет предел в точке  , и этот пределсовпадает со значением функции  .

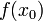• Функция непрерывна в точке, если её колебание в данной точке равно нулю.

Элементарные функции

Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.

8. Теорема о непрерывности суммы, произведения и частного функции.

Пусть функции f(x),g(x) непрерывны в точке х0. Тогда в этой точке непрерывны функции f(x)±g(x) ,f(x)g(x), f(x)/g(x) (частное в случае когда g(x0)≠0) Док. Непрерывность частного. Пусть f(x),g(x) непрерывны в точке х0, т.е. lim f(x)= f(x0) Lim g(x)=g(x0) причем g(x0)≠0 x→х0 x→х0 Существует lim (f(x)/g(x)) и тот предел равен (im f(x))/(lim g(x))=f(x0)/g(x0) x→х0 x→х0 x→х0 что означает непрерывность функции f(x)/g(x) в точке х0

9. Определение производной. Определения касательной и нормали к кривой. Геометрический смысл производной. Уравнения касательной и нормали к графику y=f(x).

ПРОИЗВОДНАЯ — производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

   Пусть даны кривая y = f(x) и точка M (x₁ ; y₁) на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).    Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x₁ ; y₁) равен значению f '(x₁) производной y' = f '(x) при x = x₁/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде

y - y₁ = f '(x₁)(x - x₁)

   Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. поэтому ее угловой коэффициент равен  , а уравнение записывается в виде

10. Таблица производных элементарных функций. Вывод производных для sin x, tg x, e^x.

 Найдем производную функции 

Дадим x приращение  , тогда   Воспользовавшись формулой преобразования разности синусов в произведение получим:

Разделим обе части этого равенства на   и перейдем к пределу при?

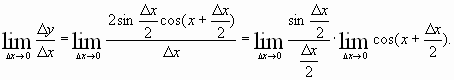
Так как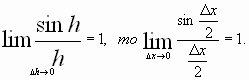 

Так как функция  непрерывна в любой точке x, то 

В итоге получаем 

Таким образом 

Аналогично выводится формула 

Воспользовавшись формулой – производная частного двух функций, найдите производные функций 

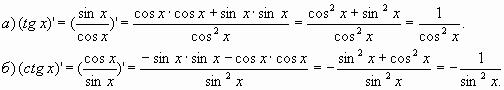
В итоге получаем 

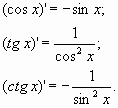
Решение :  Пусть y = u^v- общая показательная функция , где u и v – функции от переменной x , тогда прологарифмируем правую и левую части равенства, получим : lny = v *lnu, и возьмем производную , тогда получим : y’/y = v’*lnu + v*u’/u, отсюда  y’= (v’*lnu + v*u’/u)*y = (v’*lnu + v*u’/u)* u^v= u^v *v’*lnu + v*u’*u^(v-1) (*)  Рассмотрим функцию y= a^x, тогда используя обшую формулу для покательных функций (*), получим :  Y’ = (a^x)’ = a^x * lna*(x)’ = x*a^(x-1) * (a)’ = a^x * lna, так как (x)’=1, (a)’= 0.  Рассмотрим функцию y= e^x, тогда используя обшую формулу для покательных функций (*), получим :  Y’ = (e^x)’ = e^x * lne+ x*e^(x-1) * (e)’ = e^x, lne=1, (e)’= 0.  Ответ : = (a^x)’ = a^x * lna ,  (e^x)’ = e^x.

(e^x)'=lim[dx->0](e^(x+dx)-e^x)/dx=lim[dx->0]((e^x)(1-e^dx)/dx)=lim[dx->0](e^x(dx+o(dx))/dx)=e^x