Соотношение между понятиями и логические операции с понятиями.
Отношения между понятиями отражают в кругах Эйлера, где каждый круг обозначает объем понятия, а каждая точка – предмет, входящий в объем понятия.
1. Равнозначными называют такие понятия, содержания которых соответствуют друг другу, а объемы совпадают. Например, «великая русская река» и «Волга». X – Волга; R – великая русская река. (рис. 2)
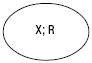
Рис. 2
2. В отношении пересечения находятся понятия, объем одного из которых частично входит в объем другого понятия. Например, «юрист» и «военнослужащий». X – юрист; R – военнослужащий. (рис. 3)
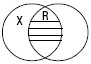
Рис. 3
В совместившейся части круга х и R (заштрихованная часть) мыслятся те юристы, которые являются военнослужащими.
3. В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, составляя его часть. Например, «преступление» и «взятка». X – преступление; R – взятка.(рис. 4)
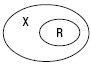
Рис. 4
Понятие, имеющее больший объем и включающее объем другого понятия, называется подчиняющим. Понятие, имеющее меньший объем и составляющее часть объема другого понятия, – подчиненным. Если в отношении подчинения находятся два общих понятия, то подчиняющее понятие называется родом, а подчиненное – видом.
Если в отношении подчинения находятся общее и единичное понятие, то общее называют видом, а единичное – индивидом. Понятия, объемы которых не совпадают ни полностью, ни частично, называются несовместимыми.
Существуют три вида несовместимости: соподчинение, противоположность, противоречие.
1. В отношении соподчинения находятся два или более неперекрещивающихся понятия, подчиненных общему для них понятию.
Например, «следователь», «адвокат» и «юрист». Z – юрист; У – следователь; X – адвокат. (рис. 5)
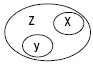
Рис. 5
2. В отношении противоположности находятся понятия, одно из которых содержит некоторые признаки, а другое эти признаки отрицает, заменяя их на противоположные. Например, «черный» и «белый». Z – черный; Р – белый. (рис. 6)
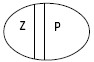
Рис. 6
3. В отношении противоречия находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает, не замещая их никакими другими признаками. В отношении противоречия находятся отрицательные и положительные понятия.
Определение. Правила определения. Классификация. Правила классификации.
Определение (дефениция) понятия – это логическая операция, раскрывающая содержание понятия или значение термина.
Правила:
1. Определение должно быть соразмерным, т.е. объем определяемого понятия должен совпадать с объемом определяющего, они должны быть равнозначащими понятиями. Эта соразмерность легко проверяется через перестановку мест членов определительного суждения. Приведем примеры. «Наука о законах и формах правильного мышления есть логика». Если переставить местами это логическое уравнение, то можно обнаружить тождество, как и в первом случае. Иное дело, когда мы прибегнем к таким примерам: «Молодой человек, обладающий дипломом, есть специалист». Если переставить местами определяемое и определяющее, то можно заметить, что понятие «специалист» шире понятия «молодой человек с дипломом». Значит, в этом случае данное правило нарушено.
2. Нельзя допускать круга в определении, т.е. когда определяющее само разъясняется через определяемое понятие. Нарушение этого правила ведет к логической ошибке – тавтологии. Вот некоторые примеры тавтологии: «Преступник – это человек, совершивший преступление»; «Сравнительная аналогия» (из газеты «Телегород», № 21, 2003). Здесь видно, что определяющее понятие повторяет сказанное в определяемом, не раскрывая его значения. Во избежание этой ошибки нужно помнить, что определяемое и определяющее понятия равны по объему, но не тождественны по своему содержанию, представляют самостоятельные понятия.
3. Определение не должно быть только отрицательным. Ведь целью определения является ответ на вопрос: чем является данный предмет, отображенный в понятии. Для этого необходимо выявить и перечислить в утвердительной форме его существенные признаки. Отрицательное определение отмечает лишь отсутствующие признаки, т.е. указывает, чем не является данный предмет. Однако негативный момент в составе определяющего понятия иногда необходим, он более четко выделяет предмет нашей мысли. Например, понятие «невидимый мир» не дает позитивного представления об этом мире, но подчеркивает сам предмет, который отображен в понятии.
4. Определение должно быть кратким, точным и ясным.
Слишком многословное определение выходит за рамки своего назначения и грозит превратиться в простое описание. В определении надо избегать двусмысленных, расплывчатых терминов, которые можно толковать по-разному. Нечеткое определение ведет к непониманию предмета, к смутным представлениям и путанице.
Точность определения предполагает его однозначность на протяжении всего рассуждения (выступления перед аудиторией, письменного текста, процесса и вывода). Этого требует логический закон тождества. В практике нередко возникает необходимость изменить определение, но при этом обязательно должна быть сделана специальная оговорка. Ясность определения зависит от его краткости и точности.
Классификация - это сложный вид деления с основанием, состоящим из нескольких признаков, включающий несколько уровней. В классификации каждый член деления получает строго определенное, единственное место в получившейся системе.
Различают следующие основные правила деления и связанные с ними ошибки:
а) в каждом делении должно быть строго определенное, единственное основание, которое не изменяется на протяжении всего деления (правило основания). Ошибка, которая при этом совершается, называется "подменой, или потерей основания". Так, нельзя делить понятие "республика" на "парламентские", "президентские" и "федеративные", поскольку здесь явно смешиваются два различных основания;
б) деление должно быть соразмерным (правило соразмерности), то есть совокупность объемов членов деления должна полностью исчерпывать объем делимого понятия. При делении не должен быть пропущен ни один предмет из объема делимого понятия и не должен появиться ни один лишний предмет. Соответственно ошибки, которые здесь могут встретиться, называются "слишком узкое деление" (когда при перечислении членов деления некоторые из них теряются, не указываются, упускаются) и "слишком широкое деление" (когда появляются лишние, не входящие в объем делимого понятия части).
в) члены деления должны взаимно исключать друг друга, быть в состоянии несовместимости (соподчинения, или субординации, противоположности, противоречия). Ошибка, которая при этом нередко допускается, называется "смешением членов деления". Она встречается в том случае, когда какой-нибудь элемент объема делимого понятия входит одновременно в объемы двух и более членов деления;
г) деление должно быть непрерывным (правило многоступенчатого деления). Все члены деления должны являться ближайшими вида-ми исходного понятия, выделяемыми по выбранному основанию. Ошибка, которая при этом может быть совершена, называется "скачок в делении". Она встречается в том случае, если члены деления не являются ближайшими видами делимого понятия, т.е. можно найти такие понятия среди членов деления, которые будут выступать видами для делимого понятия и родами для других членов деления. Для классификационного деления большое значение имеет последнее правило - правило непрерывности, поскольку классификация, как правило, включает в себя несколько (много) уровней деления, (достаточно вспомнить классификации животных и растений в биологии).