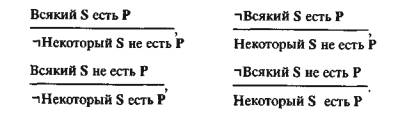15. Категорические атрибутивные высказывания: типы и структура, определение истинности.
Категорическое атрибутивное высказывание – это высказывание, в котором утверждается или отрицается наличие какого-то признака у всех или некоторых предметов рассматриваемого класса.
В категорических высказываниях утверждается или отрицается принадлежность каких-то признаков рассматриваемым предметам и указывается, идет ли речь обо всех этих предметах или же о некоторых из них. Возможны, таким образом, четыре вида категорических высказываний:
Все S есть Р – общеутвердительное высказывание, а
Некоторые S есть Р – частноутвердительное высказывание, i
Все S не есть Р – общеотрицательное высказывание, е
Некоторые S не есть Р – частноотрицательное высказывание.о
Категорические высказывания можно рассматривать как результаты подстановки каких-то имен в следующие выражения с "пробелами" (многоточиями): "Все ... есть ...", "Некоторые ... есть ...", "Все ... не есть ..." и "Некоторые ... не есть ...". Каждое из этих выражений является логической постоянной (логической операцией), позволяющей из двух имен получить высказывание. Например, подставляя вместо многоточий имена "летающие" и "птицы", получаем, соответственно, следующие высказывания: "Все летающие есть птицы", "Некоторые летающие есть птицы", "Все летающие не есть птицы" и "Некоторые летающие не есть птицы". Первое и третье высказывания являются ложными, а второе и четвертое – истинными.
Субъект- это термин, обозначающий те предметы, о которых нечто утверждается или отрицается.
Предикат- это термин, это то, что утверждает или отрицает о некотором предмете.
16.Логический квадрат. Непосредственные умозаключения по логическому квадрату.
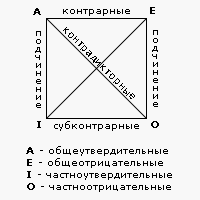
К непосредственный умозаключениям по логическому квадрату относятся умозаключения, которые строятся на основе знания отношений между высказываниями вида, SaP, SeP, SiP, SoP.
Под обращением понимают непосредственное умозаключение, в котором субъект заключения совпадает с предикатом посылки, а предикат заключения с субъектом посылки.
Различают чистое обращение, и обращение с ограничением.
Силлогистика.Виды силлогистических теорий. Законы позитивной силлогистики.
Силлогистика - это исторически первая, логическая дедуктивная теория, построенная Аристотелем.
Виды:
Традиционная силлогистика. При интерпретации термина на некотором унивёрсуме, они обязательно должны оказаться знаками таких классов, которые являются не пустыми и не универсальными.
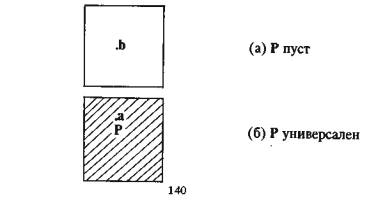
Аристотелевская силлогистика. Сходна с традиционной, но ограничения на термины не накладываются.
Позитивная силлогистика. В ней не учитывается структура терминов, они понимаются как элементарные выражения, не содержащие отрицаний. (ОТРИЦАНИЕ НЕДОПУСТИМО).
Негативная силлогистика. Используются как положительные, так и отрицательные термины.
Законы позитивной силлогистики:
Всякий S есть S – Закон тождества для высказывания а
Некоторый S есть S – Закон тождества для высказывания i
Неверно, что Всякий S не есть S
Некоторый S не есть S
Всякий S есть P. Некоторый S есть P.
Всякий S не есть P. Некоторый S не есть P. 5 и 6 –Законы подчинения.
Закон Контрарного противоречия: Всякий S есть P & Всякий S не есть P.
Закон субконтрарного исключенного третьего. Некоторые S есть P или Некоторые S не есть P.
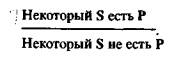
Закон противоречия для а и о . Всякий S есть P & Некоторый S не есть P.
Закон исключенного третьего для а и о. Всякий S есть P или Некоторый S не есть P
Закон противоречия для е и i. Всякий S не есть P & Некоторый S есть P.
Закон исключенного третьего для е и i. Всякий S не есть P или Некоторый S есть P
