8. Условно разделительные умозаключения. (диллемы)

Умозаключение, в котором одна посылка состоит из нескольких условных суждений, а другая является разделительным суждением, называется условно разделительным.

Умозаключения этого типа называют еще лемматическими (от греческого lemma – предложение, предположение) Это название указывает на то, что в этих умозаключениях рассматриваются (сопоставляются) различные предположения и вытекающие из них следствия. В зависимости от числа условных суждений (альтернатив) различают дилеммы, трилеммы и полилеммы. Дилемма содержит в себе две альтернативы. Трилемма – три, а полилемма – четыре и более.

Дилемма является наиболее распространенной разновидностью условно-разделительных умозаключений. Дилеммы бывают конструктивные и деструктивные. Дилемма может быть простой либо сложной.

Простая конструктивная дилемма. В условной посылке простой конструктивной дилеммы утверждается, что из двух различных оснований вытекает одно и то же следствие. В разделительной посылке утверждается, что выбор ограничен только этими двумя основаниями. В заключении утверждается следствие условных посылок.

Простая конструктивная дилемма применяется тогда, когда необходимо показать неизбежность какого-либо явления, события, решения. Данная цель достигается, когда мы показываем, что это явление может быть обусловлено двумя альтернативами, и что это – все возможные альтернативы.

9. ПОНЯТИЕ НЕПРЯМОГО СПОПОБА АРГРУМЕНТАЦИИ. ВИДЫ НЕПРЯМЫХ СПОСОБОВ АРГУМЕНТАЦИИ: рассуждение по правилу дедукции, рассуждение от противного, рассуждение сведением к абсурду, рассуждение разбором случаев).

Иногда в ходе рассуждения для обоснования некоторого высказывания применяются непрямые способы аргументации.

Непрямой способ аргументации – это приём, позволяющий делать вывод об осуществлении некоторого основного рассуждения при осуществлении одного или нескольких вспомогательных рассуждений, т.е. это переход следующего типа:

Из ▲1 выведено В1

Из ▲2 выведено В2

.

Из ▲п выведено Вп

Из Г выведено А.

Непрямой способ аргументации корректен, если и только если он гарантирует сохранение логического следования при переходе от вспомогательных рассуждений к основному, т.е. обеспечивает логическое следование А из Г, когда В1 следует из ▲1,В2 следует из ▲2,…, Вп следует из ▲п.

Несколько видов непрямых способов аргументации.

1) Рассуждение по правилу дедукции.

Из Г и А выведено В

Из Г выведено АכּВ.

2) Рассуждение от противного.

Из Г и ¬А выведено В

Из Г и ¬А выведено ¬В

Из Г выведено А

3) Рассуждение сведением к абсурду.

Из Г и А выведено В

Из Г и А выведено ¬В

Из Г выведено ¬А

4) Рассуждение разборов случаев.

Из Г и А выведено С

Из Г и В выведено С

Из Г и А▼В выведено С

10.Понятие индуктивного умозаключения.Виды индуктивных умозаключений: полная и неполная индукция, научная индукция, умозаключения по аналогии.

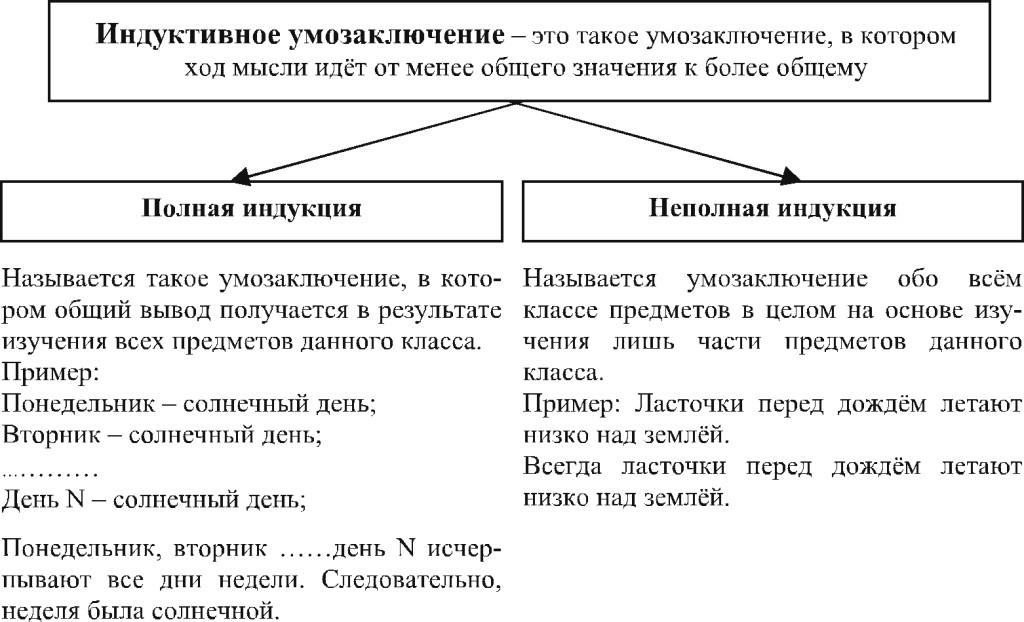
Научная индукция есть комбинация индукции и дедукции, теории и эмпирического исследования. В научной индукции основанием для вывода является не только перечисление примеров и констатация отсутствия контрпримера, но и обоснование невозможности контрпримера в силу его противоречия рассматриваемому явлению. Таким образом, вывод делается не только на основании внешних признаков, но и на представлении о сущности явления. Это означает, что нужно иметь теорию данного явления. Благодаря этому степень вероятности получения истинного вывода в научной индукции значительно повышается.

Пример. Для того чтобы убедиться в достоверности вывода «Всегда перед дождем ласточки летают низко над землей», достаточно понять, что ласточки перед дождем летают низко над землей потому, что низко летают мошки, за которыми они охотятся. А мошки летают низко потому, что перед дождем у них от влаги набухают крылышки.

Если в популярной индукции важно обозреть как можно большее число случаев, то для научной индукции это не имеет принципиального значения.

Пример. Легенда гласит, что Ньютону для открытия фундаментального закона всемирного тяготения достаточно было наблюдать один случай – падение яблока.

Значимой характеристикой умозаключения как одной из форм мышления человека является вывод нового знания. При этом в умозаключении вывод (следствие) получается в ходе движения мысли от известного к неизвестному. К такому движению человеческой мысли относятся дедукция и индукция. Наряду с ними существуют и другие виды умозаключений, одним из которых является аналогия.

Аналогия (греч. analogia – «сходство», «соответствие») представляет собой сходство, подобие предметов (явлений) в каких-либо свойствах, признаках, отношениях. Например, химический состав Солнца и Земли сходен. Поэтому когда на Солнце обнаружили еще неизвестный на Земле элемент гелий, то по аналогии сделали вывод: такой элемент есть и на Земле.

Умозаключение по аналогии опирается на ряд несомненных данных, которыми в конкретных исторических условиях располагает наука. Оно представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов (или процессов) к общности других свойств и отношений. Аналогия играет существенную роль в естественных и гуманитарных науках. Ко многим научным открытиям исследователи подошли благодаря ее использованию. Например, природа звука устанавливалась по аналогии с морской волной, а природа света – по аналогии со звуком.

Аналогия имеет свою специфику. Так, она представляет собой определенное правдоподобие исследуемого предмета (или явления) и выражает знание с внутренне скрытой вероятностью. Процесс формирования и широкого распространения аналогии начался с обыденного сознания, и она непосредственным образом связана с повседневной жизнью людей. Выводы аналогии неоднозначны, обычно они не имеют доказательной силы.

Поэтому следует переходить от вывода по аналогии к заключению по необходимости. Любая видимая аналогия нуждается в проверке посредством фактического доказательства[17] . Такое требование связано с тем, что можно получить ложный вывод, хотя он и строится согласно требованиям аналогии.

Схема умозаключения по аналогии.

А обладает признаками а, b, с, d.

В обладает признаками а, b, с.

Вероятно, В обладает признаком d.