Логика высказываний. Предметный язык логики высказываний. ( определение алфавита, формулы).
Высказывание- повествовательное предложение, истинное или ложное.
Функция высказывания-выражения, содержащие переменные и превращающиеся в высказывание при замене переменных постоянными.
Функция указатель-выражение, которое при замене переменных постоянными превращается в обозначение, описание предмета.
Высказывание истинно, если имеет значение «истина».
Высказывание ложно, если имеет значение «ложь».
Предметный язык логики высказываний состоит из алфавита и формул.
Алфавит – совокупность исходных символов данного формализованного языка.
Алфавит:
P,q,r,….-пропозициональные переменные
̚,&, V, →,↔,..-пропозициональные связки
( , )- технические символы
Формулы:
Всякая пропозициональная переменная является формулой, р-формула
Если р-формула, то ̚р-то же формула
Если р и q- формулы, то р&q, pvq, р→q, p↔q,- тоже формулы.
Ничто иное не является формулой.
Логика высказываний( пропозициональная логика)- это логическая теория, язык который содержит 1 тип нелогических символов(переменные), а так же 1 тип логических символов-связки.
3 Основные пропозициональные связки. ( определение отрицания, конъюнкции, дизъюнкции, импликации,эквивалентности). Таблицы истинности для связок.
Отрицание истинно, тогда и только тогда, когда высказывание ложно.
̚ А
Конъюнкция истинна, тогда и только тогда, когда оба высказывания истинны.
А&В
Дизъюнкция истинна тогда и только тогда, когда оба высказывания ложны.
AVB
Импликация ложна тогда и только тогда, когда из истинного антецедента следует ложный консеквент.
А→В
Эквиваленстность истинна тогда и только тогда, когда оба высказывания либо истинны, либо ложны.
А↔В
Таблица истинности связки - отражает все ситуации влияния значений элементарной переменной на значение сложного высказывания.
Пример:
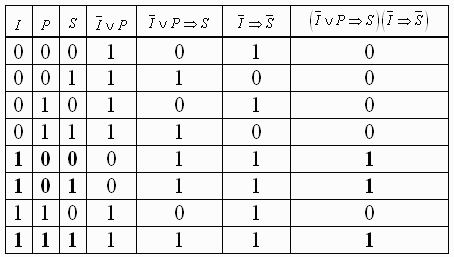
4.Алгоритм построения таблицы истинности. Виды формул логики высказываний.
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация и эквивалентность.
1) Выделяются все различные пропозициональные переменные, входящие в состав А.
2) В столбик выписываются все возможные наборы значений этих переменных.
3) В составе формулы А выделяются все подформулы (начиная с элементарных и кончая самой формулой А).
4) Вычисляется значение каждой подформулы при каждом наборе значений переменных.
Формула называется тождественно ложной тогда и только тогда, когда она принимает значение ложь при любых наборах значений, входящих в нее переменных
Формула называется выполнимой если она принимает значение истина покрайне менее при 1 наборе значений, входящих в нее переменных.