Гетерогенный катализ

Гетерогенно-каталитические реакции.

1. Понятие – процессы, протекающие на границе раздела фаз, одной из которых служит катализатор.

Гетерогенно-каталитические реакции заметно более распространены в промышленности, чем реакции гомогенного катализа. Наибольшее практическое значение получили гетерогенно-каталитические процессы на твердых катализаторах, что обусловлено удобством отделения твердого катализатора от газообразных и жидких реагентов.

Типы катализаторов.

В зависимости от физического состояния твердые катализаторы подразделяют на порошковые (зернистые), нанесенные (адсорбционные) и скелетные.

1. Зернистые катализаторы.

• представляют собой измельченные твердые тела, применяемые обычно в цилиндрической форме или в виде сферических гранул размером в несколько миллиметров.

2. Нанесенные адсорбционные катализаторы

• обычно готовят нанесением активного агента (например, ) на пористый инертный носитель с высокоразвитой поверхностью. Обычно это делают посредством пропитки активированного угля, силикагеля, алюмосиликатов и др. пористых веществ растворами солей металлов с последующей просушкой и термической обработкой или восстановлением водородом.

3. Скелетные катализаторы.

• готовят путем сплавления порошков металлов с алюминием и последующим растворением (выщелачиванием) последнего в щелочи. Остается «скелет», обладающий высокой пористостью и удельной поверхностью.

Кинетика гетерогенно-каталитических реакций

1. Закон действующих поверхностей

Химическое взаимодействие в гетерогенно-каталитическом процессе происходит между адсорбированными молекулами реагентов, как говорят, в адсорбционном слое. Тогда скорость реакции будет зависеть не от объемной, но от поверхностной концентрации реагирующих веществ, т.е. от величин адсорбции.

Скорость гетерогенно-каталитической реакции пропорциональна произведению величин адсорбции (степеней заполнения) каждого из реагентов, т.е.

2. Изотерма адсорбции Ленгмюра.

Связь между поверхностной и объемной концентрацией реагирующего вещества устанавливается изотермой адсорбции. Если принять, что поверхность катализатора энергетически однородна, т.е. , то величина адсорбции описывается уравнением Ленгмюра:

или , .

3. Кинетика мономолекулярной реакции.

,

а)

б) , т.о.

4. Кинетика бимолекулярной реакции.

.

а)

б) , т.о.

Кинетика реакций в растворах . Уравнение Бренстеда – Бьеррума.

Клеточный эффект

Молекулы растворённого вещества совершают нерегулярные колебания с периодом τ ₀ в “клетке”, образованной соседними молекулами растворителя. Поколебавшись около одного положения равновесия в течение некоторого времени τ , частица перескакивает в соседнюю клетку, для чего она должна иметь энергию, большую некоторого порогового значения E. В рамках клеточной модели механизм жидкофазной реакции выглядит следующим образом: каждая из частиц скачками, следующими друг за другом через время τ , беспорядочно перемещается в среде растворителя. В результате перемещений происходят случайные встречи частиц, то есть попадание их в одну клетку жидкости, с образованием диффузионной пары. В клетке частицы испытывают колебания с периодом τ_o , во время которых они претерпевают соударения с молекулами растворителя и между собой. Если за время τ частицы не успевают прореагировать, то диффузионная пара распадается, и частицы снова расходятся. Таким образом, необходимым условием жидкофазной реакции является предварительное попадание частиц в результате диффузии в одну клетку, где частицы и реагируют в соударениях.

Время пребывания в клетке обычно составляет 10^–10 – 10^–8с.

Влияние ионной силы на скорость реакции.

Уравнение Аррениуса справедливо и для реакций в растворах. В этом уравнении и во всех уравнениях химической кинетики фигурируют кон­центрации реагирующих веществ. В термодинамике же констан­та равновесия неидеальной системы выражается через активно­сти. Это обстоятельство необходимо учитывать, если в кинети­ческое уравнение входит константа равновесия. Правда, при ре­акциях в газовой фазе и между нейтральными молекулами в рас­творе в этом нет практической необходимости, но при рассмо­трении реакций между заряженными частицами подобное пре­небрежение может явиться источником существенных ошибок. Для константы скорости бимолекулярной реакции

протекающей в растворе, теория активного комплекса дает

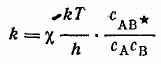
Т ермодинамическая же константа равновесия между исходными веществами и активным комплексом

И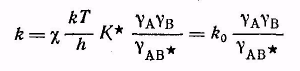 , комбинируя эти уравнения, получаем

Это уравнение Бренстеда-Бьеррума.

Оно справедливо для константы скорости реакции, протекающей в любой неидеальной среде. Величина k₀ имеет смысл константы скорости при бесконечном разведении, т. е. при γ=1.

Д ля использования уравнения в конкретном случае необходимо задаться тем или другим аналитическим выраже­нием для коэффициентов активности. Если в качестве стандартного состояния выбрать бесконечное разведение, теория элек­тролитов дает следующее приближенное соотношение для коэффициента активности:

Рассмотрим два случая:

1. Взаимодействие между заряженными ча­стицами. Д ля случая взаимодействия между двумя ионами второй сомножитель мал, и тогда

Следовательно, логарифм константы скорости, согласно тео­рии, должен быть линейной функцией корня квадратного из ионной силы, а тангенс угла наклона прямой определяется соотношением зарядов реагирующих частиц.

2. Взаимодействие между ионом и нейтраль­ной молекулой: z = 0.

Согласно уравнению, коэффициент активности для нейтральной молекулы: γ=e^βI

М алость величины β позволяет разложить экспоненту в ряд, пренебрегая членами высших степеней для не очень больших значений I:

Следовательно, константа скорости пропорциональна ионной силе.

При рассмотрении р-ций в растворах следует учитывать, что, хотя число столкновений реагирующих частиц с растворителем очень много, эти столкновения увеличивают как скорость активации, так и скорость дезактивации. Поэтому в целом скорость реакции меняется мало – увеличивается или уменьшается до двух раз. НО есть исключения: типичный случай – реакция Меншуткина: R-X (Х – галоген) + N - (R_i)₃ = X – N – (R_i)₄ . Скорость этой реакции сильно зависит от растворителя. Очень малая часть соударений приводит к реакции – стерический множитель от 10^-5 до 10^-8. Причины – необходима специфическая ориентация при столкновении, имеется специфическое распределение энергии по внутренним степеням свободы.