8.2. Поиск.
Напомним что:
Пролог использует быстрый, но глупый (неэффективный) метод поиска. Написание программы своего поиска не так сложно.
Семейное Дерево.
% - parent ( A, B) истина, если A является родителем B
parent( p1, p2 ).
parent ( p3, p2 ).
parent ( p2, p4 ).
parent ( p4, p5 ).
8.2. Поиск.
Напомним что:
Пролог использует быстрый, но глупый(неэффективный) метод поиска. Написание программы своего поиска не так сложно.
Семейное Дерево.
% - parent ( A, B) истина, если A является родителем B
parent( p1, p2 ).
parent ( p3, p2 ).
parent ( p2, p4 ).
parent ( p4, p5 ).
8.2.1 Поиск в Прологе.
Основные стратегии поиска:
Поиск в глубину ( исследуется первый путь до конца перед переходом на следующий путь )
Поиск в ширину ( исследуются сначала все самые близкие пути)
Наиболее лучшего ( использует величину "оценки")
8.2.2 Поиск в глубину.
Отслеживайте узлы, которые еще не исследовались (т.н " " открытые " " узлы ).
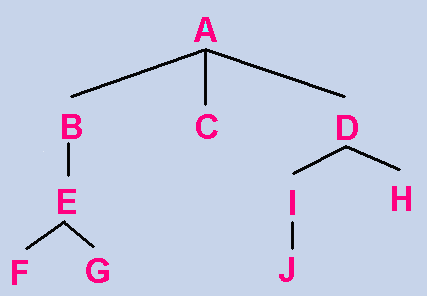
search(X, X, T).
search(X, Y, T) :- (edge(X, Z); edge(Z, X)),
not(member(Z, T)),
search(Z, Y, [Z|T]).
member(X, [X|_]) :- !.
member(X, [_|Y]) :- member(X, Y).
edge(a,b).
edge(a,c).
edge(a,d).
edge(b,e).
edge(e,f).
edge(e,g).
edge(d,h).
edge(d,i).
edge(i,j).
Другой вариант
depth_first(Start, Answer ) :-
depth_star(/*Open*/ [Start], Answer ),!.
depth_star( [X|_], X ).
depth_star( [X|Open1], Y ) :-
children(X, Children),
append( Children, Open1, Open2 ),
depth_star( Open2, Y ).
/*children(A,Bs) is true if A*/
/*is parent of each child in Bs*/
children(a, [b,c,d]).
children(b, [e]).
children(e, [f,g]).
children(d, [h,i]).
children(i, [j]).
/* a f */
Обратите Внимание: открытый список хранится ,как стек.
Обратите Внимание на представление:
То есть мы можем представлять граф, как
%-- children(A,Bs) истина если A
%-- является родителем каждого ребенка в Bs
children(p1, [p2]).
children(p3, [p2]).
children(p2, [p4]).
children(p4, [p5]).
Мы можем также представить обратное отношение
parents(p2, [p1, p3]).
parents(p4, [p2]).
parents(p5, [p4]).
8.2.3 Поиск в ширину.
Подобен поиску в глубину , но хранит открытый список, как очередь.
breadth_first( Start,Answer ) :-
breadth_star(/*Open*/ [Start],
Answer ).
breadth_star( [X|_], X ).
breadth_star( [X|Open1], Y ) :-
children(X, Children),
append( Open1, Children, Open2 ),
breadth_star( Open2, Y ).
children(a, [b,c,d]).
children(b, [e]).
children(e, [f,g]).
children(d, [h,i]).
children(i, [j]).
8.2.4 Резюме Поиска.
Поиск в Прологе использует самую простую (самый дешевую) стратегию.
Другие алгоритмы поиска можно написать на Прологе.
Эффективность - частая проблема в поиске .
Чем меньше узлов Вы посетите,тем лучше.
9.1. Введение
Поиск в графах при решении задач, как правило, невозможен без решения проблемы комбинаторной сложности , возникающей из-за быстрого роста числа альтернатив. Эффективным средством борьбы с этим служит эвристический поиск. Один из путей использования эвристической информации о задаче - это получение численных эвристических оценок для вершин пространства состояний. Оценка вершины указывает нам, насколько данная вершина перспективна с точки зрения достижения цели. Идея состоит в том, чтобы всегда продолжать поиск, начиная с наиболее перспективной вершины, выбранной из всего множества кандидатов. Именно на этом принципе основана программа поиска с предпочтением.