5.3.2 Метод пузырька.

Это простой и эффективный метод.

Декларативное описание:

1. Найти в списке L два смежных элемента X и Y, таких, что X > Y, поменять их местами и получить новый список, M, затем отсортировать M. Для поиска таких элементов и перестановки используется процедура swap/2.

2. Если в списке нет не одной пары смежных элемента X и Y, таких, что X > Y, считать что список отсортирован.

busort(L, S) :- swap(L, M), !, busort(M, S). busort(L, L) :- !. swap([X, Y|R], [Y, X|R]) :- order(Y, X). swap([X|R], [X|R1]) :- swap(R, R1).

5.3.3 Mетод вставки.

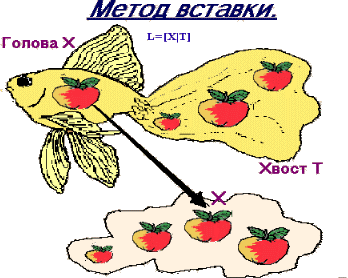
Декларативное описание:

Для того чтобы упорядочить непустой список L=[X|T] необходимо:

1. Упорядочить хвост Т списка L

2. Вставить голову X списка L в упорядоченный хвост, поместив ее таким образом, чтобы получившийся список остался упорядоченным.

insort([], []). insort([X|L], M) :- insort(L, N), insortx(X, N, M). insortx(X, [A|L], [A|M]) :- order(A, X), !, insortx(X, L, M). insortx(X, L, [X|L]). order(X, Y) :- X =< Y.

5.3.4 Быстрая сортировка quick.

Описание метода:

Убираем первый элемент:

5 3 7 8 1 4 7 6

получаем: X =5. и оставшийся список:

3 7 8 1 4 7 6

Разбиваем новый список на два, помещая в первый элементы меньше X, а во второй - больше X:

( X: 3 1 4 ) X: 7 8 7 6

Сортируем оба списка:

1 3 4 6 7 7 8

Соединим первый список, X, второй список.

1 3 4 5 6 7 7 8

Декларативное описание:

1. Удалить из списка голову Х и разбить оставшийся список на два списка Small и Big следующим образом: все элементы большие чем Х помещаются в Big и меньшие X - в Small.

2. Отсортировать список Small в Small1.

3. Отсортировать список Big в Big1.

4. Соединить списки Small1 Х и Big1.

qsort([], []). qsort([H|Tail], S) :- split(H, Tail, Small, Big), qsort(Small, Small1), qsort(Big, Big1), append(Small1, [H|Big1], S). order(X, Y) :- X =< Y. split(H, [A|Tail], [A|Small], Big) :- order(A, H), !, split(H, Tail, Small, Big). split(H, [A|Tail], Small, [A|Big]) :- split(H, Tail, Small, Big). split(_, [], [], []).

6.1 Отрицание как неудача. (not as failure)

Рассмотрим сначала пример.

		Пусть некоторая Мэри любит всех животных. Это записывается: likes(mary,X):-annimal(X).

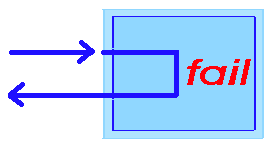
Мэри не любит змей: likes(mary,X):-snake(X),!,fail. fail - специальная цель, встроенный предикат, который всегда терпит неудачу.

Графически предикат изображается:

	Можно записать в виде одного правила, используя дизъюнкцию целей. likes(mary,X):-snake(X),!,fail; annimal(X).

Посмотрим другой пример.

Отношение different(X,Y) будет истина,если X и Y различны. (не сопоставимы).

		different(X,X):-!,fail. или different(X,Y):-X=Y,!,fail. different(X,Y).

Если X и Y сопоставимы, то цель different терпит неудачу. Иначе X и Y различны, и цель different успешна.

Или в одном предложении

different(X,Y):-X=Y,!,fail;true.

Здесь true - встроенный педикат, который всегда истина.

И в том и другом случае более удобно указывать, что отношение истинно, если цель ложна. Для этой цели используется предикат not.

not(Goal). -истина, если Goal -ложь, и наоборот not(Goal) ложно, если Goal успешна. Это можно записать:

not(Goal):-Goal,!,fail;true.

Запись аналогична сделанным, поэтому наши примеры можно переписать:

likes(mary,X):-annimal(X),not(snake(X)). или different(X,Y):-not(X=Y).

!	Использование not требует осторожности, т.к. определяется через отсечение.

Рассмотрим пример:

r(a). g(b). p(X):-not(r(X)).

?-g(X),p(X). yes ?-p(X),g(X). no.