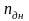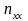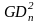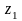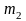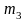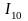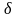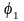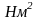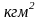- •Дифференцирование приведенного момента инерции по углу поворота и построение графика его производной.
- •Определение приведенного момента сил к валу кривошипа и построение его графика функции от угла поворота. Расчет среднего значения момента сил сопротивления и выделение его переменной части.
- •Определение динамической ошибки по углу и скорости и построение их графиков.
- •Определение неравномерности вращения начального звена при сравнении его с допускаемым.
- •Определение динамического момента на выходном валу передаточного механизма и построение его графика. Сравнение динамического момента со средним значением момента сил сопротивления.
- •3.4 Установка противовесов на главном валу машины
Санкт-Петербургский государственный политехнический университет
Каферда ТММ
Пояснительная записка к курсовому проекту
«Динамическое исследование машинного агрегата»
Выполнил студент группы 3033/1 Река А.Г.______________
Принял преподаватель, доц., к.т.н., Чубаков П.М.___________
Санкт-Петербург
2012
Содержание:
Исходные данные……………………………………………………………………………………………………………………………………………………………………………3
Введение………………………………………………………………………………………………...............................................................................................................................4
Динамическое исследование машинного агрегата………………………………………………………………………………………………………5
Определение приведенного момента инерции машинного агрегата к валу кривошипа и построение его графика функции от угла поворота кривошипа. Расчет среднего значения момента инерции и нахождение его переменной составляющей…………………………………………………………5
Дифференцирование приведенного момента инерции по углу поворота и построение графика его производной………………………………………………………………………………………………………………………………………….7
Определение приведенного момента сил к валу кривошипа и построение его графика функции от угла поворота. Расчет среднего значения момента сил сопротивления и выделение его переменной части…………………………………………………………………………………………………………………………7
Определение среднего значения угловой скорости кривошипа используя дифференцальное уравнение движения с учетом статической характеристики двигателя………………………………….....8
Определение возмущающих моментов на валу кривошипа и построение его графика. Разложение возмущающих моментов в ряд Фурье с точностью до двух гармоник и построение его графика…………………………………………………………………………………………………………………………………………....9
Определение динамической ошибки по углу и скорости и построение их графиков………………..10
Определение неравномерности вращения начального звена при сравнении его с допускаемым……………………………………………………………………………………………………………………………………………………………………..1.2
Определение динамического момента на выходном валу передаточного механизма и построение его графика. Сравнение динамического момента со средним значением момента сил сопротивления………………………………………………………………………………………………………………………………………………………..12
УРАВНОВЕШИВАНИЕ СИЛ ИНЕРЦИИ, ДЕЙСТВУЮЩИХ НА СТАНИНУ И ФУНДАМЕНТ МАШИНЫ………………………………………………..13
Приложение………………………………………………………………………………………………………………………………………………………………………………..15
1.Исходные денные:
Двигатель |
Передаточный механизм |
Исполнительный механизм |
||||||||||||||||||||
N |
|
|
|
|
|
m |
Н |
|
|
|
|
|
|
|
|
|
||||||
квт |
Об/мин |
|
|
мм |
мм |
кг |
|
Об/мин |
|
град |
||||||||||||
3.0 |
2800 |
3000 |
0,14 |
12 |
34 |
4 |
130 |
100 |
0 |
8 |
12 |
15 |
0,1 |
470 |
|
30 |
||||||
Введение:
Целью курсового проекта является динамическое исследование машинного агрегата.
Задачей динамического исследования является определение закона движения исполнительного механизма, исследование динамики машинного агрегата в установившемся движении (определение динамических ошибок параметров движения главного вала машины), определение динамических нагрузок на выходном валу привода.
В качестве исходных данных для проектирования задана схема машинного агрегата, состоящего из электродвигателя с короткозамкнутым ротором, передаточного механизма в виде зубчатой передачи и исполнительного механизма. Геометрические параметры исполнительного механизма, массы и моменты инерции его звеньев. Для двигателя задана номинальная мощность Nдн , номинальное число оборотов nдн и число оборотов холостого хода nxx, а также маховый момент ротора двигателя GDp2 .
При выполнении расчетов звенья механизмов считаются абсолютно жесткими, работа двигателя описывается статической характеристикой, трение и зазоры в кинематических парах не учитываются.
Динамическое исследование машинного агрегата
Первой задачей динамического исследования является определение закона движения вала кривошипа в установившемся режиме работы. Данная задача будет сведена к нахождению динамических ошибок по положению ψ(t) и по скорости ψ’(t).
Вторая задача заключается в определении динамических нагрузок в передаточном механизме, возникающих вследствие неравномерности вращения главного вала машины. Эти нагрузки представляют собой переменную составляющую движущего момента и приводят к циклическим изменениям напряжений в звеньях механизма.
Для решения поставленных задач необходимо построить одно-массовую модель машинного агрегата при этом считаем, что все массы звеньев являются константами, звенья являются абсолютно жесткими, зазоры в кинематических парах отсутствуют и механизм имеет одну степень подвижности. При этом в качестве обобщенной координаты, которая определяет положение всех звеньев, выбираем угол поворота φ1 вала кривошипа
Определение приведенного момента инерции машинного агрегата к валу кривошипа и построение его графика функции от угла поворота кривошипа. Расчет среднего значения момента инерции и нахождение его переменной составляющей.
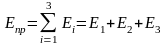 (2.1)
(2.1)
Определим приведенный момент массы или приведенный момент инерции:
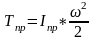 (2.2)
(2.2)
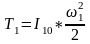 (2.3)
(2.3)
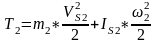 (2.4)
(2.4)
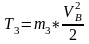 (2.5)
(2.5)
Подставим выражения (2.2),(2.3),(2.4),(2.5) в (2.1):
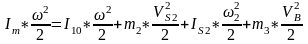 (2.6)
(2.6)
Преобразуем
выражение (2.6), поделив обе части на
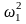 и сократив на 2:
и сократив на 2:
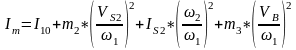
 (2.7)
(2.7)
Выражение (2.7) после преобразования перепишем в виде:
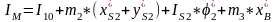 (2.8)
(2.8)
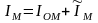 (2.9)
(2.9)
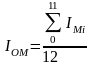 (2.10)
(2.10)
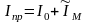 (2.11)
(2.11)
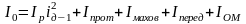 (2.12)
(2.12)
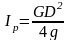 (2.13)
(2.13)
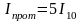 (2.14)
(2.14)
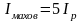 (2.15)
(2.15)
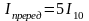 (2.16)
(2.16)
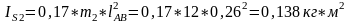 (2.17)
(2.17)
Подставим численные значения в выражения (2.16), (2.14), (2.13), (2.15):
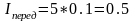
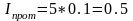
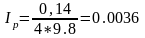
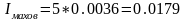
Подставим численные значения в выражение (2.8) для угла 30°:
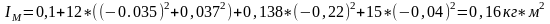
Значения
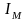 для остальных положений приведено в
таблице №1 (приложение 1)
для остальных положений приведено в
таблице №1 (приложение 1)
Подставим из таблицы [1] численные значения в выражение (2.10):
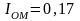
Подставим численные значения в выражения (2.9), (2.12) для угла 30°:
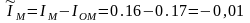
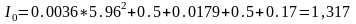
Значение приведенного момента инерции для остальных положений приведено в таблице [1]
Дифференцирование приведенного момента инерции по углу поворота и построение графика его производной.
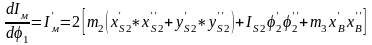 (2.18)
(2.18)
Подставим численные значения в выражение (2.18) для угла 210°:
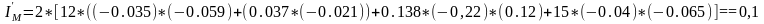
Значения производной приведенного момента инерции для остальных положений сведены в
таблицу №1 (приложение 1)
Определение приведенного момента сил к валу кривошипа и построение его графика функции от угла поворота. Расчет среднего значения момента сил сопротивления и выделение его переменной части.
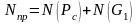 (2.19)
(2.19)
Поскольку силы веса малы по сравнению с силой сопротивления, мы пренебрегаем силами веса:
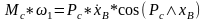 ,
(2.20)
,
(2.20)
где
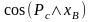 =1,
=1,
т.е.
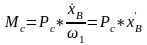 (2.21)
(2.21)
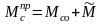 (2.22)
(2.22)
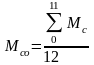 (2.23)
(2.23)
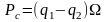 (2.24)
(2.24)
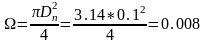 (2.25)
(2.25)
Подставим численные значения в выражение (2.24), (2.21) для угла 30°:
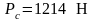
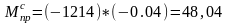
Подставим численные значения в выражения (2.23), (2.22):
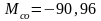
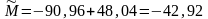
Определение среднего значения угловой скорости кривошипа используя дифференциальное уравнение движения с учетом статической характеристики двигателя.
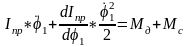 (2.26)
(2.26)
Уравнение решим методом последовательных приближений:
Представим, что машина движется с ω=const:
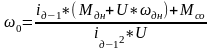 (2.29)
(2.29)
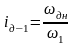 (2.30)
(2.30)
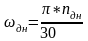 (2.31)
(2.31)
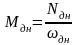 (2.32)
(2.32)
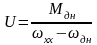 (2.33)
(2.33)
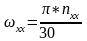 (2.34)
(2.34)
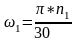 (2.35)
(2.35)
Подставим численные значения в выражения (2.34), (2.31), (2.35):
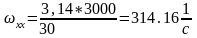
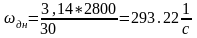
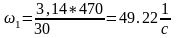
Подставим численные значения в выражения (2.32), (2.30):
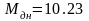
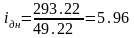
Подставим численные значения в выражение (2.33):
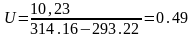
Подставим численные значения в выражение (2.29):
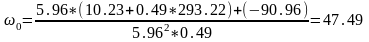
Определение возмущающих моментов на валу кривошипа и построение его графика. Разложение возмущающих моментов в ряд Фурье и построение его графика.
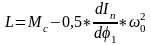 (2.36)
(2.36)
Подставим численные значения в выражение (2.36) для угла 30°:
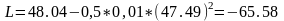
Возмущающий момент является периодической функцией и его можно разложить в ряд Фурье:
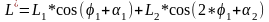 (
2.37)
(
2.37)
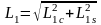 (2.38)
(2.38)
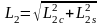 (2.39)
(2.39)
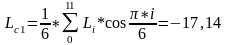 ,
i=0,1,2,…,11
(2.40)
,
i=0,1,2,…,11
(2.40)
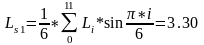 (2.41)
(2.41)
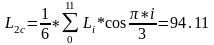 (2.42)
(2.42)
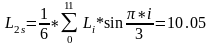 (2.43)
(2.43)
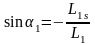 (2.44)
(2.44)
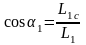 (2.45)
(2.45)
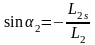 (2.46)
(2.46)
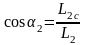 (2.47)
(2.47)
Подставим численные значения в выражения (2.38), (2.39), (2.44), (2.45), (2.46), (2.47):
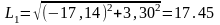
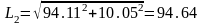
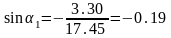
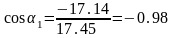
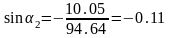
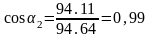
Отсюда
видно что: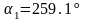 и
и
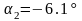
Подставим численные значения в выражение (2.37) для угла 30°:
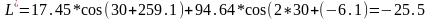
Результаты сведены в таблицу №1 (приложение 1)