- •Глава 4. Основы интегрального исчисления
- •§1.Понятие первообразной и неопределенного
- •Пример 1. Найти первообразные для функции , проходящие через точки м(2;4) и м(0;3). Сделать рисунок.
- •§2. Свойства неопределенных интегралов
- •§3. Таблица основных неопределенных интегралов
- •§4. Общие методы интегрирования
- •Метод введения нового аргумента.
- •2. Метод подстановки.
- •Несколько примеров интегралов, не выражающихся через элементарные функции
- •О технике интегрирования
- •§5. Понятие определенного интеграла
- •§6. Основные свойства определенного интеграла
- •Свойство 6
- •Свойство 7
- •Свойство 8
- •§7. Определенный интеграл с переменным верхним пределом Формула Ньютона - Лейбница
§4. Общие методы интегрирования
Meтод 1. Непосредственное интегрирование
► Отыскание неопределенных интегралов с помощью свойств интегралов,
таблицы интегралов и алгебраических, тригонометрических преобразо-
ваний подынтегральной функции называется непосредственным интег-
рированием.
Предлагаем ниже таблицу различных типовых преобразований подынтегральной функции, после которых громоздкие, на первый взгляд, интегралы, сводятся к табличным:
Таблица №5
Алгебраические преобразования подынтегральной функции
|
Свойство дроби
|
|
Свойства степени
|
|
|
Тригонометрические формулы
|
|
Пример 4. Найти неопределенные интегралы:
а)
 ;
б)
;
б)
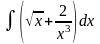 ;
в)
;
в)
 .
.
Решение.
а)
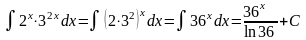 (применили
свойства степени
,
);
(применили
свойства степени
,
);
б)
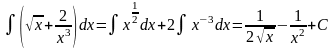 (применили
свойство степени
(применили
свойство степени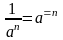 ,
и
свойства неопределенного интеграла);
,
и
свойства неопределенного интеграла);
в)
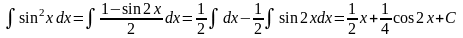 (применили
формулу
).
(применили
формулу
).
Метод 2. Метод замены переменной
Применение теоремы об инвариантности формул интегрирования к
нахождению первообразной называют методом замены переменной.
Существуют следующие варианты этого метода: метод введения новой переменной и метод постановки.
Метод введения нового аргумента.
Если под знаком интеграла стоит произведение двух функций, причем одна из них является производной от второй или её промежуточного аргумента, то за переменную интегрирования можно взять функцию, производная от которой стоит под знаком интеграла.
Во многих случаях введение нового аргумента (переменной) интегрирования позволяет свести вычисление данного интеграла к нахождению табличного.
Теорема 5. Пусть функция t = φ(x) определена, непрерывна и дифференци-
руема на некотором промежутке Х и пусть Т – множество значе-
ний этой функции, на нем.
Пусть на множестве Т определена функция , для
которой
существует первообразная
 т. е.
т. е.
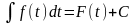 .
.
Тогда
всюду на множестве Х
для
функции
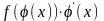
существует
первообразная функция, равная
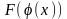 ,
т.е.
,
т.е.
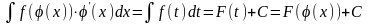 .
(1)
.
(1)
Доказательство.
Так
как F¢(t)
= f(t),
t
= φ(x),
то по
правилу дифференцирования сложной
функции
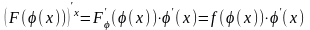
и, следовательно, первообразная от f(φ(x))φ/( x) есть F(φ(x)), т. е.
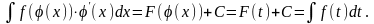
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Замечание.
После вычисления интеграла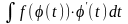 нужно перейти к
нужно перейти к
переменной х.
Пример
5. Найти
неопределенный интеграл
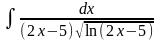 .
.
Решение.
Так как под интегралом стоит произведение двух функций
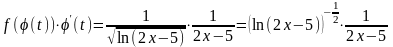 ,
,
введем
новую переменную
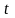 .
.
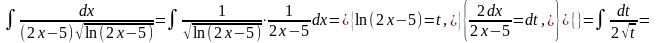
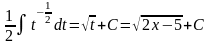 .
.
2. Метод подстановки.
Если подынтегральная функция такова, что трудно выделить производ-
ную от какого либо промежуточного аргумента или его просто нет, то в этом
случае переменную интегрирования лучше заменить некоторой другой
функцией,
полагая
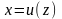 ,
дифференцируя, получаем
,
дифференцируя, получаем
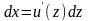 ,
(предполагается, что
,
(предполагается, что
 и
и
 непрерывны). Тогда
непрерывны). Тогда
 ,
,
где
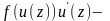 новая
функция от
аргумента
новая
функция от
аргумента
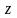 .
.
Если последний интеграл в результате такой замены свелся к таблич-
ному
и равен
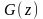 + C,
то заданный интеграл определяют путем
возвращения к переменной х,
т.е. из уравнения
надо
найти обратную функцию
+ C,
то заданный интеграл определяют путем
возвращения к переменной х,
т.е. из уравнения
надо
найти обратную функцию ,
и заменить
на
φ(х).
,
и заменить
на
φ(х).
С помощью подстановок такого рода удается избавится от корня, упро-
стить подынтегральную функцию и свести интеграл к табличному. Однако,
общего рецепта для выбора функции нет. В каждом конкретном случае
её подбирают индивидуально по виду подынтегрального выражения.
Пример
6. Найти
интеграл
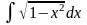 .
.
Решение.
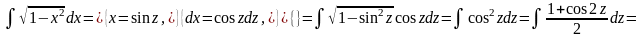
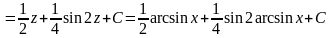 .
.
Все дальнейшее изложение темы «Неопределенный интеграл» будет состоять в основном из рассмотрения различных подстановок.
Метод 3. Интегрирование по частям
Способ интегрирования по частям основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu.
Проинтегрировав,
получаем:
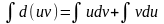 ,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
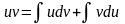 или
или
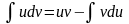 .
(3)
.
(3)
Получили формулу (3) интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Формула
(3) используется в тех случаях, когда
подынтегральное выражение f
(x)dx
можно
так представить в виде udv
,
что стоящий в правой части интеграл при
надлежащем выборе выражение u
и
dv
может
оказаться проще исходного интеграла.
Как правило, подынтегральное выражение
f(x)dx
представлено
в виде произведения различных по типу
функций, например:
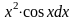 ,
,
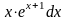 ,
,
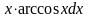 и т.д. При
этом следует иметь ввиду, что к u
следует
относить множители, которые упрощаются
при дифференцировании. В соответствии
с этим можно предложить следующую
вспомогательную таблицу.
и т.д. При
этом следует иметь ввиду, что к u
следует
относить множители, которые упрощаются
при дифференцировании. В соответствии
с этим можно предложить следующую
вспомогательную таблицу.
Обозначения частей подынтегрального выражения.
Таблица №6
f (x)dx |
u |
dv |
|
|
|
|
|
|
|
|
|
|
|
|
Пример
7.
Найти интеграл
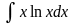 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.
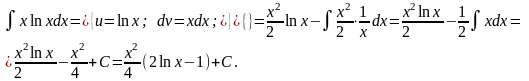
Таблицей можно воспользоваться и в случае если подынтегральная функция содержит либо только логарифмическую, либо только обратно - тригонометрическую.
Пример
8.
Найти интеграл
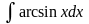 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.

! Формулу интегрирования по частям можно применять многократно, пока не упростятся подынтегральные функции, которые приведут к табличному интегралу.
Пример
9.
Найти интеграл
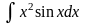 ,
применив интегрирование по частям.
,
применив интегрирование по частям.
Решение.
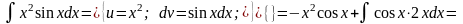
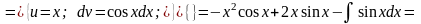
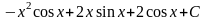 .
.
Как видно из примера 9 происходит неоднократное, последовательное применение формулы интегрирования по частям, что позволяет в итоге постепенно упростить функцию и привести интеграл к табличному.


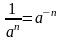
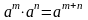
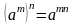
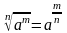
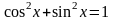 ;
;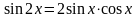 ;
;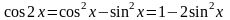 ;
; ;
;
 ;
;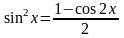 ;
;
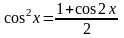 ;
;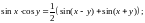
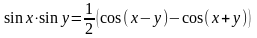 ;
;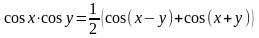
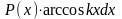 ,
,
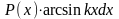 ,
,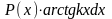 ,
,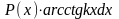
 ,
,
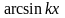 ,
,
 ,
,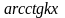
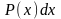 -
где
-
где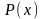 многочлен любой степени
многочлен любой степени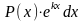
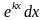


 ,
,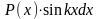 ,
,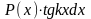 ,
,
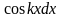 ,
, ,
,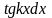 ,
,