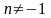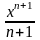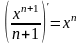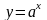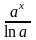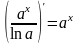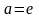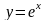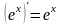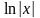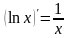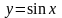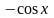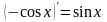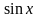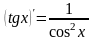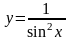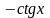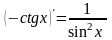- •Глава 4. Основы интегрального исчисления
- •§1.Понятие первообразной и неопределенного
- •Пример 1. Найти первообразные для функции , проходящие через точки м(2;4) и м(0;3). Сделать рисунок.
- •§2. Свойства неопределенных интегралов
- •§3. Таблица основных неопределенных интегралов
- •§4. Общие методы интегрирования
- •Метод введения нового аргумента.
- •2. Метод подстановки.
- •Несколько примеров интегралов, не выражающихся через элементарные функции
- •О технике интегрирования
- •§5. Понятие определенного интеграла
- •§6. Основные свойства определенного интеграла
- •Свойство 6
- •Свойство 7
- •Свойство 8
- •§7. Определенный интеграл с переменным верхним пределом Формула Ньютона - Лейбница
Глава 4. Основы интегрального исчисления
![]() Интегральное
исчисление
возникло из потребности создать общий
метод разыскания площадей, объемов и
центров тяжести. В зародышевой форме
такой метод применялся еще Архимедом.
Систематическое развитие интегрального
исчисления было получено в 17-м веке, в
тесной связи с возникшим тогда же
дифференциальным исчислением.
Символ
интеграла (рис.55) введен Лейбницем (1675
г.). Этот знак является изменением
латинской буквы S (первой буквы слова
сумма).
Интегральное
исчисление
возникло из потребности создать общий
метод разыскания площадей, объемов и
центров тяжести. В зародышевой форме
такой метод применялся еще Архимедом.
Систематическое развитие интегрального
исчисления было получено в 17-м веке, в
тесной связи с возникшим тогда же
дифференциальным исчислением.
Символ
интеграла (рис.55) введен Лейбницем (1675
г.). Этот знак является изменением
латинской буквы S (первой буквы слова
сумма).
Рис.55.
Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования "восстанавливает" функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное:
слово integer означает целый. В ходе переписки Бернулли и Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли. Другие известные термины, относящиеся к интегральному исчислению, появились значительно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее "примитивная функция", которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как "начальный": F(x) - начальная (или первоначальная, или первообразная) для функции f(x), которая получается из F(x) дифференцированием. В современной литературе множество всех первообразных для функции f(x) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. Название и обозначение определенного интеграла ввел К. Фурье (1768-1830 г.г.), но пределы интегрирования указывал уже Эйлер.
§1.Понятие первообразной и неопределенного
интеграла
При изучении дифференцирования функций, ставилась задача - по данной функции найти ее производную или дифференциал.
Например, если закон движения какого-либо тела задан уравнением вида
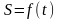 ,
,
где
t
—
время, а S
— пройденный телом путь, то
дифференцированием функции
 мы
находим мгновенную скорость
мы
находим мгновенную скорость
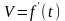
этого
движения в данный момент времени. Однако
в механике гораздо чаще приходится
встречаться с обратной задачей: для
любого момента времени t
дана скорость тела
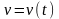 ;
требуется найти закон движения тела,
т. е. зависимость пройденного им пути
от времени. Как мы можем подойти к решению
этой задачи и многих других, которые
приводят к постановке обратной задачи
-
для данной функции f(x)
найти такую функцию F(x),
производная или дифференциал которой
равны соответственно f(x)
или f(x)dx?
Дадим определение функции F(x).
;
требуется найти закон движения тела,
т. е. зависимость пройденного им пути
от времени. Как мы можем подойти к решению
этой задачи и многих других, которые
приводят к постановке обратной задачи
-
для данной функции f(x)
найти такую функцию F(x),
производная или дифференциал которой
равны соответственно f(x)
или f(x)dx?
Дадим определение функции F(x).
► Функция F(x) называется первообразной по отношению к функции f(x)
на некотором множестве X, если на этом множестве функция F(x)
дифференцируема и удовлетворяет уравнению
F¢(x) = f(x)
или,
dF(x) = f(x)dx.
Так,
например, функция
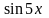 – первообразная на любом промежутке
по отношению к функции
– первообразная на любом промежутке
по отношению к функции
![]() ,
так как
,
так как
![]() .
Аналогично из тождества
.
Аналогично из тождества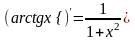 следует, что функция
следует, что функция
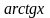 является первообразной по отношению к
функции
является первообразной по отношению к
функции
![]() .
.
Таким образом, основываясь на знании таблицы производных основных элементарных функций можно составить таблицу.
Таблица базовых первообразных.
Таблица№3
Тип функции |
Функция
|
Первообразная
|
|
Степенная |
|
|
|
Показательная |
|
|
|
|
,
при
|
|
|
Логарифмическая |
|
|
|
Тригонометрическая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратно - тригонометрическая |
|
|
|
|
|
|
|
Легко проверить, используя правила дифференцирования, что наличие одной первообразной обеспечивает наличие таких функций в бесконечном множестве.
Теорема
1.
Если
 и
и
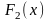 –
две первообразные для функции
–
две первообразные для функции
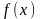 на
на
данном множестве, то они могут отличаться лишь на посто-
янную,
т.е.
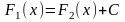 ,
где C
–
постоянная.
,
где C
–
постоянная.
Доказательство:
Положим
 .
.
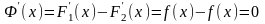 ,
следовательно
,
следовательно
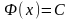 .
.
Действительно
 .
.
На вопрос, как найти все первообразные данной функции, если известна одна из них, дает ответ следующая теорема.
Теорема 2 (о первообразных).
Если F(x) - одна из первообразных функции f(x) на
заданном множестве, то все ее первообразные имеют вид
F(x) + С, где С– произвольная постоянная.
Геометрически y = F(x) + C означает, что график любой первообразной функции получается из графика функции y = F(x) простым сдвигом его параллельно оси ОУ на величину С (см. рисунок 56). График первообразной от функции f (x) называется интегральной кривой этой функции, поэтому
неопределенный интеграл геометрически представляется множеством всех
интегральных кривых, получаемых при непрерывном параллельном движении одной из них по вертикали.

Рис.56.
В связи с тем, что одна и та же функция f(x) имеет бесконечно много первообразных, возникает проблема выбора первообразной, которая решает ту или иную практическую задачу.

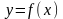
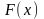
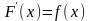
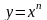 ,
кроме
,
кроме