Цель работы

1.Исследование системы электропитания с регулируемым источником.

2.Оптимизация параметров системы электропитания с целью повышения качества регулирования и улучшения характеристик переходных процессов и стационарных режимов.

Описание системы

Принципиальная схема системы электропитания приведена на рис.1. Ее образуют:

- основной источник Е_О ;

- регулируемый источник Е_Р ;

- датчик Д текущего значения регулируемой переменной;

- регулятор Р с уставкой X_уст номинального значения регулируемой переменной;

- исполнительный механизм ИМ , обеспечивающий изменение ЭДС Е_Р.

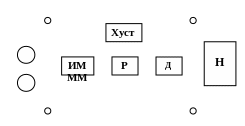
Рис.1. Принципиальная схема системы питания

Эквивалентная схема замещения нагрузки приведена на рис.2. Регулируемой переменной является ток i , протекающий через резистор R.

Параметры нагрузки: R_O=1.5 Ом, R=1.0 Ом, С=1000 мкФ.

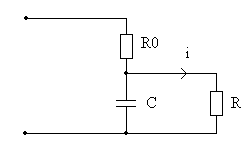
Рис.2.Схема замещения нагрузки

Для элементов цепи регулирования используются следующие эквиваленты:

1. датчик – пропорциональное звено с коэффициентом усиления К_Д;

2. регулятор – инерционное звено первого порядка с коэффициентом усиления К_Р и постоянной временя Т_Р;

3. исполнительный механизм – инерционное звено первого порядка с коэффициентом усиления К_им и постоянной времени Т_им.

Параметры цепи регулирования: К_им=0.9 , Т_им=0.002 с , Т_р=0.001 с .

Номинальное значение регулируемой переменной в установившемся режиме: 100А.

Расчет параметров звена, эквивалентирующего нагрузку.

1. Операторный метод

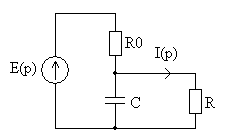
2. Физическое пространство

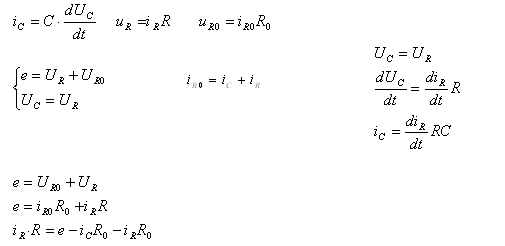
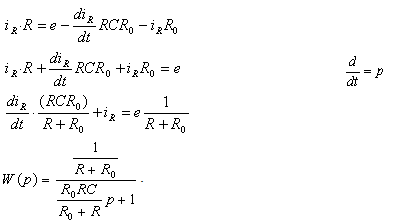
По передаточной функции видно, что это инерционное звено 1 порядка. Найдем численное значение его параметров.

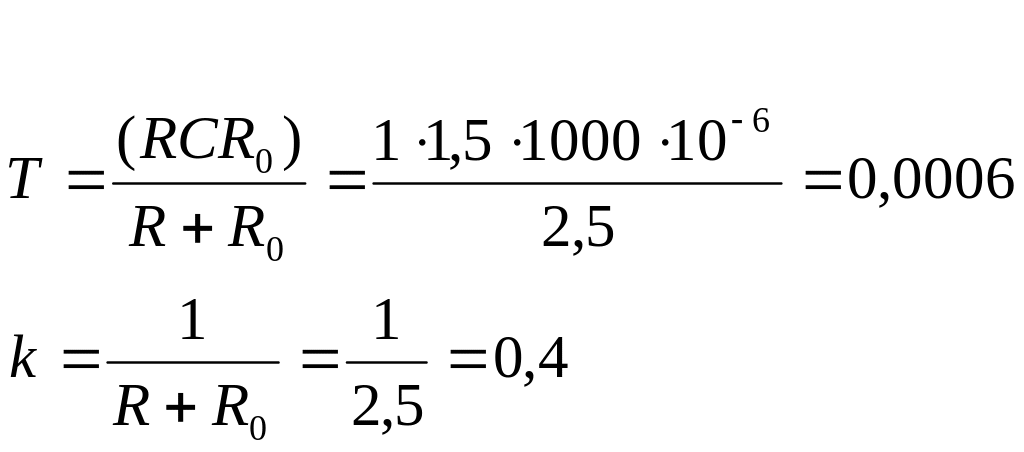
Расчет величины эдс Ео основного источника

1. методом расчета расчета установившегося режима системы питания и нагрузки

Е_Р=0 I=100 А R_э=Ro+R=2.5 Ом

Е_о=I*R_э=250 В

2. используя передаточную функцию звена нагрузки

Теоретическая и экспериментальная переходные характеристики звена нагрузки

Теоретическая переходная характеристика:

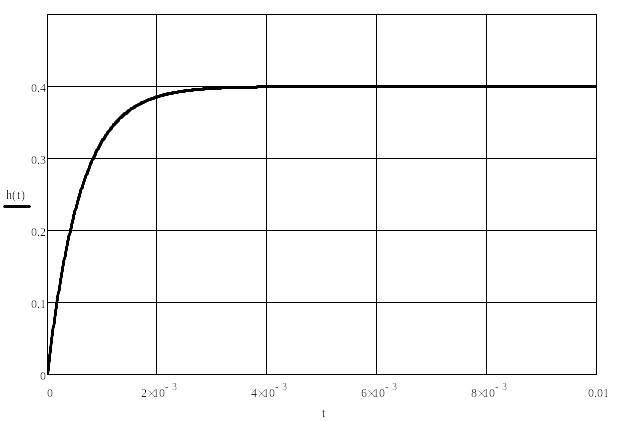
Экспериментальная переходная характеристика:

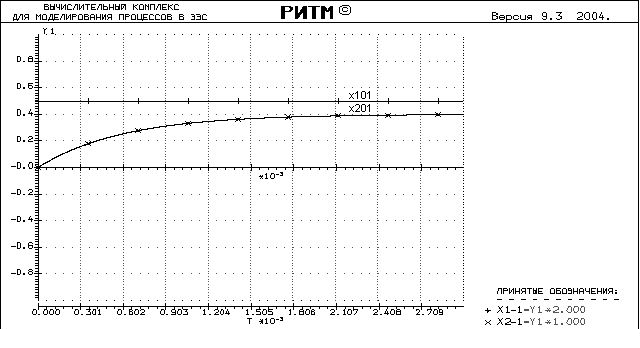
Определение параметров звена по экспериментальной переходной характеристике

K=h( =0.4

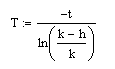
Тестовый расчет, подтверждающий правильность определения величины ЭДС Ео

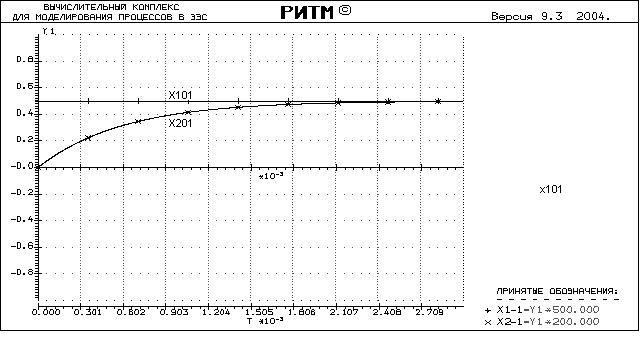
Построение аналитической амплитудно-фазовой частотной характеристики звена, эквивалентирующего нагрузку.

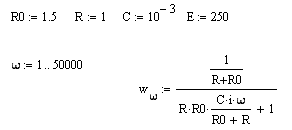
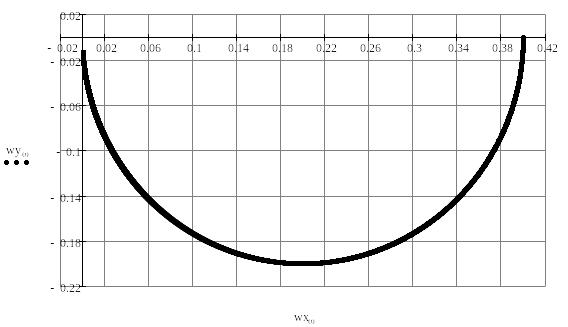
Таблица значений, необходимых для проведения серии расчетов, позволяющих построить экспериментальную амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку.

ω, рад/с	f, Гц	T, мс	Tуст, мс	Tокн, мс	h,мкс
555.5555556	88.4194115	11.3097337	56.5486686	73.5132692	113.0973372
1026.4696034	163.3677089	6.1211607	30.6058035	39.7875446	61.21160703
1507.5567229	239.9351009	4.1677937	20.8389685	27.090659	41.67793692
2151.6574146	342.4469083	2.9201607	14.6008034	18.9810445	29.20160689
3333.3333333	530.5164691	1.8849556	9.4247781	12.2522115	18.8495562
10408.329997	1656.5371439	0.6036689	3.0183446	3.92384802	6.036689268

где ω – частота гармонического сигнала (рад/с)

f – частота гармонического сигнала (Гц)

Т – период колебаний

T_уст – время окончания переходного процесса

T_окн – время окончания расчета

h – шаг расчета

Экспериментальная амплитудно-фазовая частотная характеристика

Схема имитационной модели:

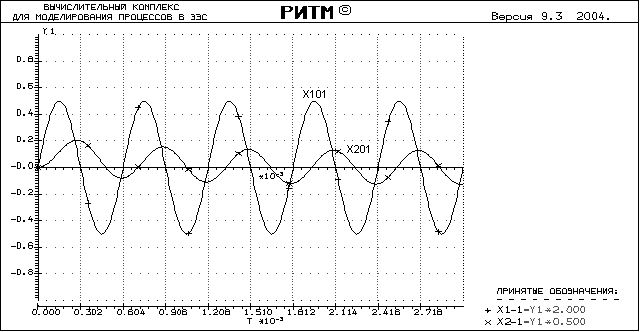
Осциллограмма выходного и входного сигнала при частоте f=1656.5371 Гц

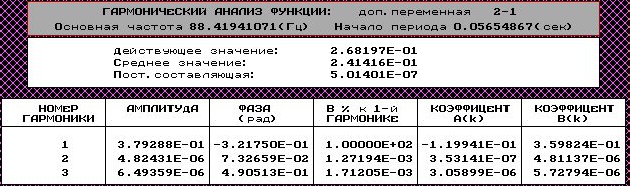
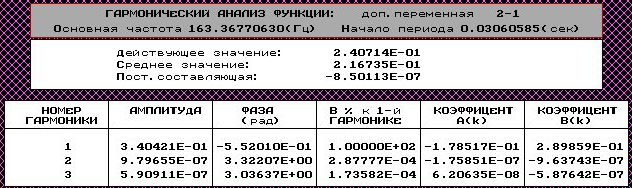
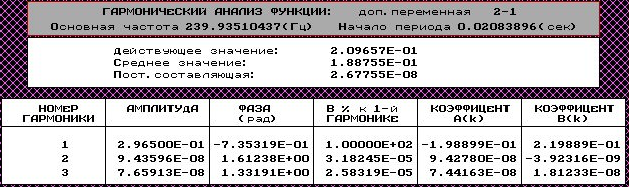
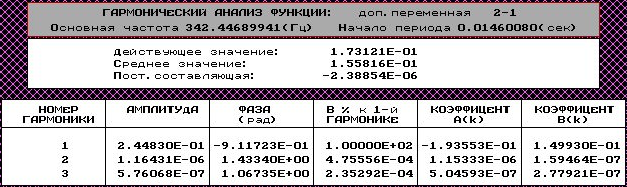
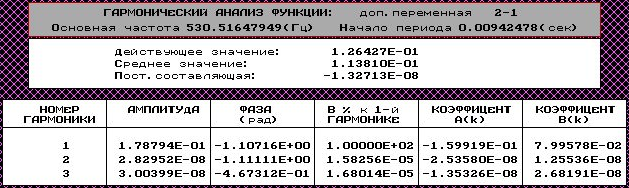
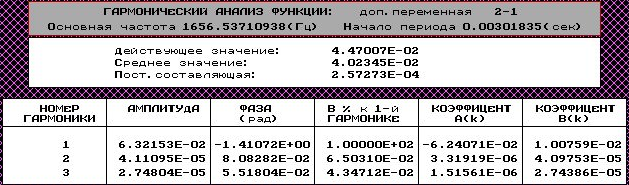
Значения полученные экспериментально:

Xmi	i	w`	w``
0.379288	-0.32175	0.3598243	-0.1199412
0.340421	-0.55201	0.289859	-0.1785167
0.2965	-0.735319	0.2198894	-0.1988992
0.24483	-0.911723	0.1499301	-0.1935528
0.178794	-1.10716	0.0799573	-0.1599191
0.0632153	-1.41072	0.0100761	-0.0624071

Пример расчета для первой строки

где X_mi – амплитуда выходного сигнала

_{i – ­}фаза выходного сигнала

w` - вещественная часть АФЧХ

w`` - мнимая часть АФЧХ

Сравнение аналитической и экспериментально полученной АФЧХ.

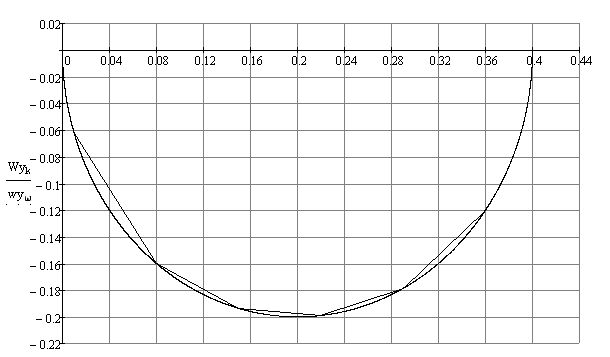
Аналитически и экспериментально полученные АФЧХ совпадают, что свидетельствует о правильности сделанных расчетов.

Структурная алгоритмическая схема системы автоматического управления

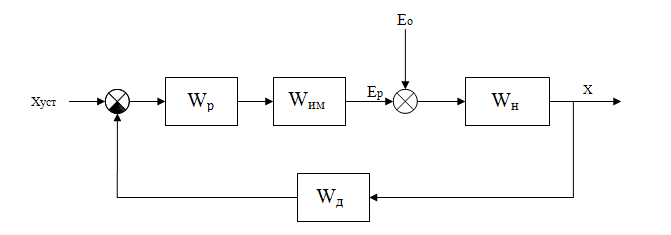
где W_Р – передаточная функция звена, эквивалентирующего регулятор

W_ИМ – передаточная функция звена, эквивалентирующего исполнительный механизм

W_Н – передаточная функция звена, эквивалентирующего нагрузку

W_Д – передаточная функция звена, эквивалентирующего датчик текущего значения регулируемой переменной

Область устойчивости системы

Найдем эквивалентную передаточную функцию САУ относительно Е_О и X_УСТ

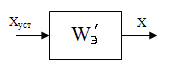
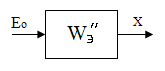
1) 2)

Преобразуем схему:

П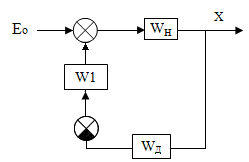 реобразуем схему:

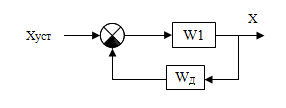
где W1=W_PW_ИМ W_Н

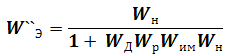
Возьмем передаточную функцию относительно Е_О и подставим все передаточные функции, входящие в нее.

После упрощения получаем выражение:

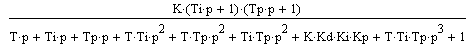
Характеристическое уравнение является знаменателем передаточной функции

Зная характеристическое уравнение найдем область устойчивости

3 причины нарушения устойчивости:

1. а_n=0

2. a_o=0

3. Δ_n-1=0

где a_o – коэффициент при высшей степени полинома

а_n - свободный член полинома

Δ_n-1 – предпоследний определитель Гурвица

В нашем случае а_n= K*Kd*Ki*Kp+1

a_o= T*Ti*Tp

Подставим известные значения:

Полученные выражения приравниваем к нулю и таким образом получаем два уравнения связывающие коэффициенты K_р и K_d.

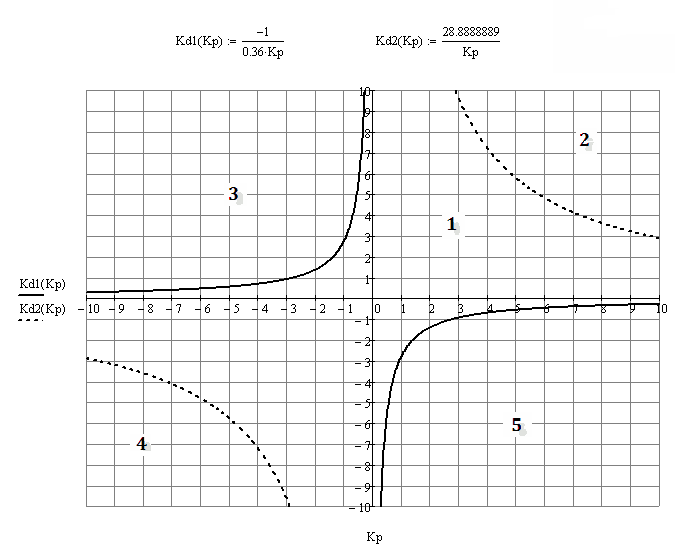
Таким образом получили 5 областей. Найдем в каких областях САУ устойчиво: для этого из каждой области возьмем по одной точке и воспользовавшись критерием устойчивости Гурвица проверим каждую область.

Критерий устойчивости Гурвица:

Необходимым и достаточным условием устойчивости является положительность определителя Гурвица и всех его диагональных миноров.

1область К_р=1 , К_д=1

Получаем следующие значения коэффициентов

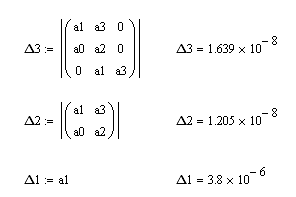
Все коэффициенты больше нуля, что говорит о том, что данная область устойчива.

Для проверки найдем корни уравнения:

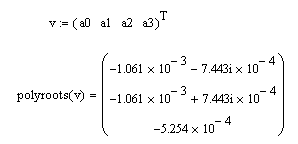
Вещественные части всех корней получились отритцательными, что подтверждает устойчивость.

2область К_р=10 , К_д=10

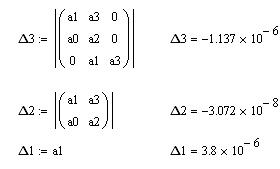
Не все определители положительны, поэтому система в этой области неустойчива

К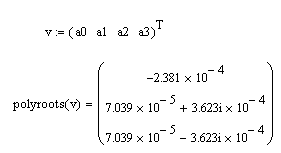 орни уравнения:

Есть корни с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.

3 область К_р= 10 , К_д=10

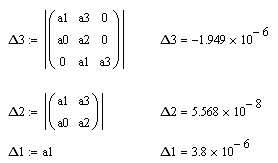
Не все определители положительны, поэтому система в этой области неустойчива

Корни уравнения:

Есть корень с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.

4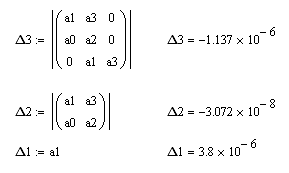 область К_р= 10 , К_д= 10

Не все определители положительны, поэтому система в этой области неустойчива

Корни уравнения:

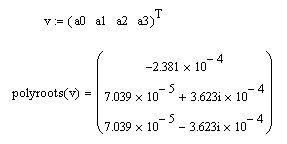
Есть корни с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.

5 область К_р=10 , К_д= 10

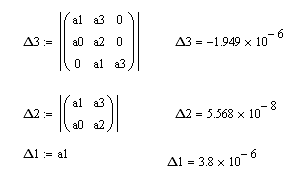
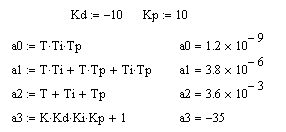
Не все определители положительны, поэтому система в этой области неустойчива

Корни уравнения:

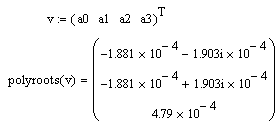
Есть корень с положительной вещественной частью, что говорит о том, что система в данной области неустойчива.

Таким образом единственной устойчивой областью является первая.

Имитационная модель системы автоматического управления

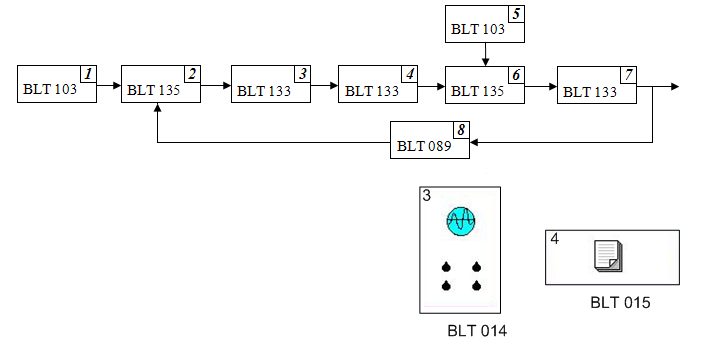
Используемые блоки:

BLT089 – пропорциональное звено;

BLT103 – источник кусочно-постоянного сигнала;

BLT133 – инерционное звено первого порядка;

BLT135 – сумматор;

BLT014 – осциллограф;

BLT015 – табулятор.

Из первой устойчивой области берем точку К_Д=0,1 , К_Р=1

Таким образом параметры блоков имеют следующие значения

3 К=1 Т=0,001

4 К=0,9 Т=0,002

7 К=0,4 Т=0,0006

8 К=0,1

Полученная осциллограмма:

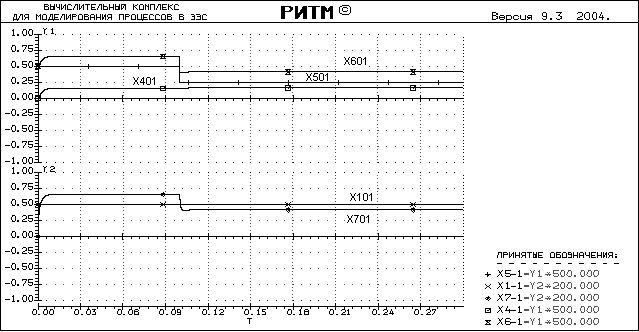
Видно, что при данных настройках системы требуемое условие Е_Р=0 в установившемся режиме не выполняется. Внесем некоторые изменения в структуру системы. После 1 блока поставим пропорциональное звено с коэффициентом усиления равным коэффициенту усиления звена, эквивалентирующего датчик.

Таким образом получаем новую имитационную модель САУ.

.

Параметры блоков:

3 К=1 Т=0,001

4 К=0,9 Т=0,002

7 К=0,4 Т=0,0006

8 К=0,1

9 К=0,1

Полученная осциллограмма:

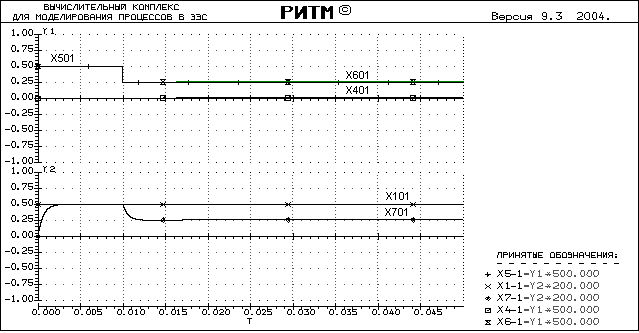
Из осциллограммы видно, что величина ЭДС Е_Р регулируемого источника в статическом режиме уходит в ноль, но статизм системы очень плохой.

Подберем такой коэффициент К_Р( при фиксированном К_Д=0,1), при котором обеспечивается 5% статизм системы.

где – статизм

- изменение выходной величины

- изменение внешнего воздействия

В нашем случае ( после потери 50% ЭДС основного источника Е=250 В)

Тогда

Т.е. для обеспечения 5% статизма выходная величина ( переменная X701) должна в установившемся режиме выйти на значение 100-100*0,0625=93,75 ( при номинальном значение = 100)

Теоретическое определение коэффициента К_р , обеспечивающего 5% статизм.

x=w*f

где x – выходная величина

f – внешнее воздействие

w – передаточная функция

Поскольку у нас 2 передаточных функции воспользуемся методом наложения

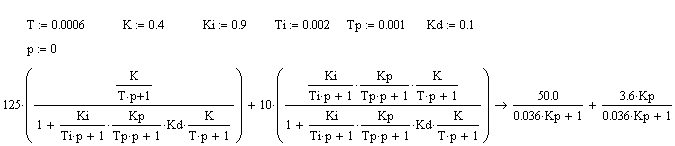
Упрощаем выражение и приравниваем его к 93,75

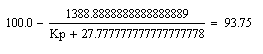
Отсюда находим что К_Р=194,444 .

Это значение попадает в область устойчивости

Имитационная модель

Параметры блоков:

3 К=194,444 Т=0,001

4 К=0,9 Т=0,002

7 К=0,4 Т=0,0006

8 К=0,1

9 К=0,1

Полученная осциллограмма:

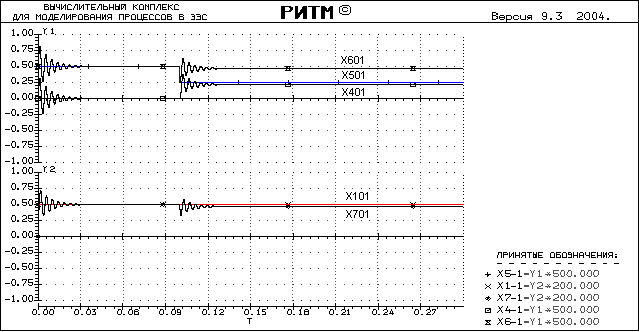
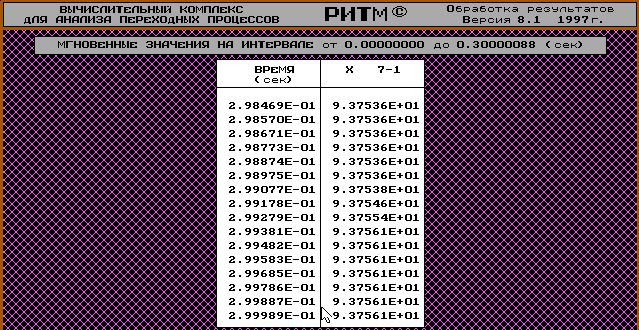
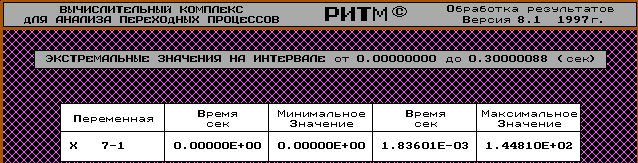
Видно что теоретически найденное значение К_Р обеспечивает нужный статизм с хорошей точностью.

Но при данном значении параметра плохое перерегулирование σ=44,81 %

Подберем такое значение К_Р при котором перерегулирование будет 25 %.