Пункт 13.

Попробуем получить статизм и перерегулирование, не превышающие допустимых значений, изменяя параметры настройки. Поскольку в доаварийном режиме нам необходимо, чтобы в установившемся режиме = 0 , то изменять параметр датчика мы не можем, следовательно, необходимо изменять параметр . Т.о. фиксируем ,а значение будем изменять в пределах области устойчивости. Ниже представлены два графика, полученные расчетом имитационной модели (изображенной в п.10), для обеспечения наилучших показателей статизма и перерегулирования.

1.Возьмем

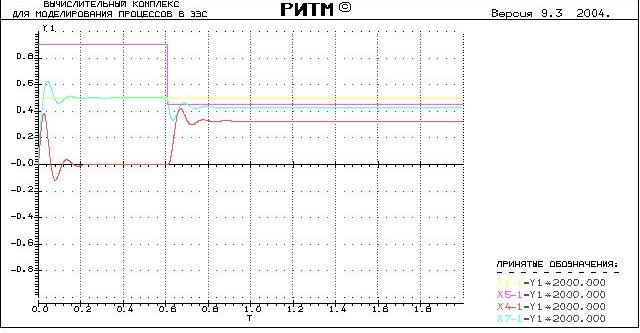
2. Возьмем

В результате получили:

при , =15.1% и = 25.5% - получили перерегулирование, попадающее в допуск 30%, но статизм > 5%. Увеличили . Получили, что при , =9.3% и = 40.9%, статизм уменьшился, но еще > 5%, а значение перерегулирования возросло и вышло за рамки допуска.

При =4.8% и = 66.3% - значение статизма удовлетворяет допуску.

Т.о. видно, что при увеличении статизм уменьшается, а перерегулирование увеличивается, значит вариацией мы не можем одновременно добиться нужных нам значений и перерегулирования, и статизма. В таком случае возьмем значения настроек , которые обеспечивают значение перерегулирования, не превышающее 30%.

Для улучшения статизма используем астатическое управление, т.е. введем интегрирующее звено в цепь обратной связи, так чтобы оно попало в слаботочную цепь.

Получаем следующую структурную алгоритмическую схему САУ.

Передаточная функция интегрирующего звена

Wинт =

Эквивалентируем относительно .

Эквивалентная передаточная функция САУ относительно

При подстановке p = 0 видно, что данная система обладает нулевым статизмом:

Для выбора значения коэффициента нужно пересчитать область устойчивости системы в плоскости коэффициентов и при .

Из знаменателя:

при замене р на получаем характеристический полином

,

с коэффициентами

Для определения области устойчивости используем критерий Гурвица.

Для построения границ областей устойчивости используем следующие уравнения:

1.

Т.е. = 0

или .

2.

Т.о. используя следующие зависимости:

, .

строим область устойчивости.

2

6

1

5

4

3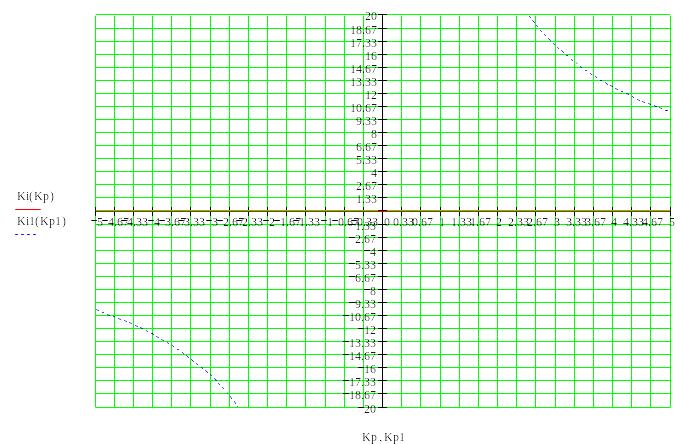

Получили 6 области, теперь проверим, какая из них является устойчивой.

Рассмотрим область 1, возьмем

Область 1 не является устойчивой, т.к не выполняется условие и

Рассмотрим область 2,возьмем

Область 2 также не является устойчивой, т.к. не выполняются условия .

Рассмотрим область 3.

Возьмем

Область 3 является устойчивой, т.к. выполняются условия устойчивости, а именно положительность определителя Гурвица и всех его диагональных миноров.

Рассмотрим область 4, возьмем

Область 4 является устойчивой, т.к. выполняется условия устойчивости критерия Гурвица.

Рассмотрим область 5.

Возьмем

Область 5 не является устойчивой, т.к. не выполняется условие .

Рассмотрим область 6,возьмем

Область 6 не является устойчивой, т.к не выполняется условие и .

В результате выяснения областей устойчивости мы определили, что 3 и 4 области являются областями устойчивости нашей системы. В таком случае выберем значения

= 4 и = 2.67 из области устойчивости. После построения имитационной модели получим процесс, отображенный на следующей осциллограмме.

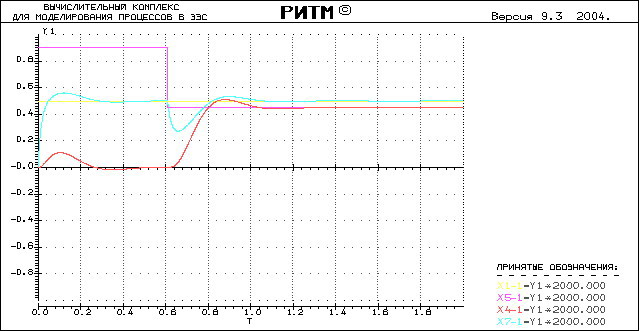
Показатели качества данной САУ:

1.перерегулирование

2.статизм

Полученные значения перерегулирования и статизма не превышают допустимых значений.

3.длительность переходного процесса

До и после аварии длительности переходного процесса не одинаковы, т.к. до аварии основной вклад в длительность процесса вносит генератор, т.е. , а после аварии на длительность переходного процесса большее влияние оказывает . Подберем так, чтобы длительности были одинаковы. Возьмем близкое к , т.е. = 2.3.

Тогда теоретическое время за которое выходная величина достигла 95 % до и после аварии составляет 0.31с

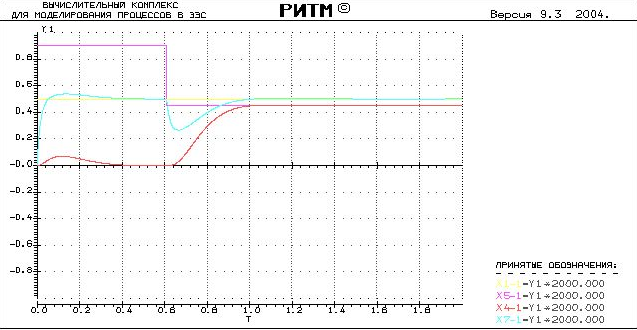
Опытное время составило 0.25с.