Министерство образования Российской Федерации

Санкт-Петербургский Государственный Политехнический Университет

Электромеханический факультет

Кафедра ТВН, Электроснабжение

Курс “Теория автоматического регулирования”

Пояснительная записка

Вариант № 1

Выполнили: студенты группы 3021/3

Забурчик Н. А.,

Невзоров И. В.

Преподаватель: Попков Е. Н.

Санкт-Петербург

2007

Материалы к учебной работе по курсу

"Теория автоматического регулирования"

Вариант: 1

Цель работы

1. Исследование системы электропитания с регулируемым источником.

2. Оптимизация параметров системы электропитания с целью повышения качества регулирования и улучшения характеристик переходных процессов и стационарных режимов.

Описание системы

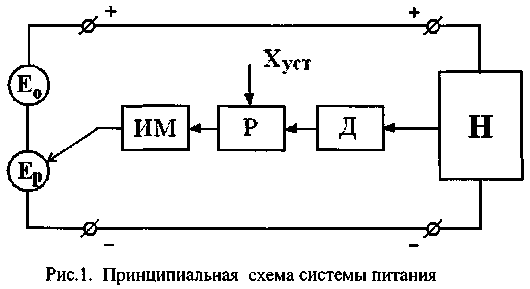
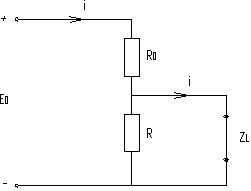
Принципиальная схема системы электропитания приведена на рис.1. Ее образуют:

- основной источник Е0;

- регулируемый источник Ер ;

- датчик Д текущего значения регулируемой переменной;

- регулятор Р с уставкой Хуст номинального значения регулируемой переменной;

- исполнительный механизм ИМ , обеспечивающий изменение э.д.с. Ер.

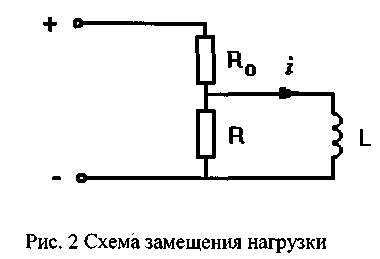
Эквивалентная схема замещения нагрузки приведена на рис.2. Регулируемой переменной является ток i катушки индуктивности L .

Параметры нагрузки: R0= 1.8 Ом , R = 8.8 Ом , L = 0.024 Гн .

Для элементов цепи регулирования использовать следующие эквиваленты:

1) датчик - пропорциональное звено с коэффициентом усиления Кд;

2) регулятор - инерционное звено первого порядка с коэффициентом усиления Кр и постоянной времени Тр;

3) исполнительный механизм - инерционное звено первого порядка с коэффициентом усиления Ким и постоянной времени Тим.

Параметры цепи регулирования: Ким = 0.9 , Тим = 0.04 с. , Тр = 0.01 с .

Номинальное значение регулируемой переменной в установившемся режиме: 1 кА .

Выполнение курсовой работы.

Пункт 1.

Представить нагрузку системы питания в виде звена, для которого входным сигналом является напряжение на зажимах источника питания, а выходным сигналом - указанная регулируемая переменная. Получить описание звена в виде сокращенной записи дифференциального уравнения и передаточной функции. Установить тип звена и рассчитать численные значения параметров.

Физическое пространство:

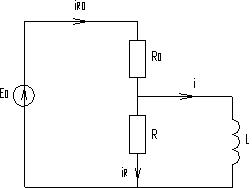
Составим систему уравнений на основе первого и второго закона Кирхгофа и закона Ома:

Операторное пространство:

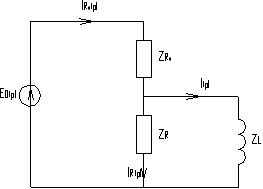
Имеем апериодическое звено 1-го порядка(инерционное звено 1-го порядка).

Пункт 2.

а) Определение величины э.д.с. Е0 основного источника методом расчета установившегося режима системы питания и нагрузки.

,

б) Определение величины э.д.с. Е0 основного источника, используя передаточную функцию звена.

Пункт 3.

Построение аналитической переходной характеристики звена, эквивалентирующего нагрузку.

Пункт 4.

Получение на ЭВМ переходной характеристики звена, эквивалентирующего нагрузку. Используем вычислительный комплекс «РИТМ».

1) BLT 103 – источник кусочно-постоянного сигнала

2) BLT 133 – инерционное звено первого порядка

3) BLT 014 – осциллограф

4) BLT 015 – табулятор

Х1-входной сигнал звена (единичное ступенчатое воздействие)

Х2-сигнал на выходе звена - переходная характеристика звена (реакция звена на единичное ступенчатое воздействие).

Аналитическая переходная характеристика звена и построенная в РИТМе совпадают.

Определение параметров звена по экспериментальной переходной характеристике:

(совпадает с аналитическим k=0.556)

=0.310742, =0.01312

= (отличие от аналитического значения составляет 0.193%)

Пункт 5.

Выполнение тестового расчета, подтверждающего правильность определения э.д.с. Е₀

Вместо источника единичного ступенчатого сигнала включаем в цепь источник с найденным аналитически значением ЭДС (Е₀=1800В).

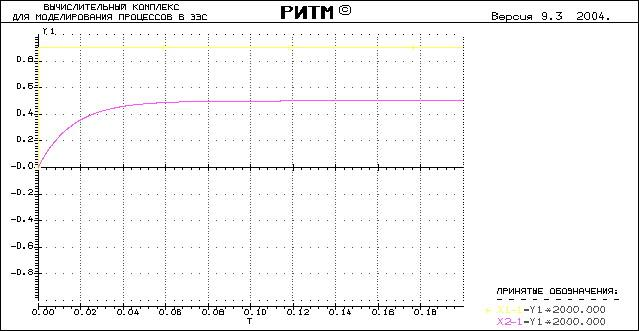
Х1- входной сигнал звена

Х2-сигнал на выходе звена

При выполнении тестового расчета было получено значение выходного сигнала, равное1000,80 А, что отличается от номинального значения регулируемой величины ( ) на 0.08%.

Пункт 6.

Построение аналитической амплитудно-фазовой частотной характеристики звена, эквивалентирующего нагрузку.

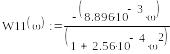
Пункт 7.

Построение экспериментальной АФЧХ звена, эквивалентирующего нагрузку.

Схема имитационной модели:

1) BLT 091 – генератор гармонического сигнала

2) BLT 133 – инерционное звено первого порядка

3) BLT 014 – осциллограф

4) BLT 015 – табулятор

Таблица значений для расчетов, необходимых для построения АФЧХ звена, эквивалентирующего нагрузку:

ω, рад/с	f,Гц	,c	Т,с	Ток	Тга	h	Xm	φ,рад	W'	W''
350.374399	55.763817	0.016061	0.017933	0.107597	0.089664	0.000161	0.097282	-1.394925	0.017021	-0.095781
167.965088	26.732474	0.016061	0.037408	0.224446	0.187038	0.000161	0.19326	-1.215803	0.067174	-0.18121
105.296616	16.758477	0.016061	0.059671	0.358028	0.298356	0.000161	0.28299	-1.036783	0.14404	-0.24359
61.468104	9.782953	0.016061	0.102219	0.613312	0.511093	0.000161	0.395677	-0.778965	0.28158	-0.27798
36.362805	5.78732	0.016061	0.172792	1.036749	0.863958	0.000161	0.480125	-0.528578	0.4146	-0.24213
19.127184	3.044186	0.016061	0.328495	1.97097	1.642475	0.000161	0.531482	-0.298044	0.50805	-0.15607
7.372086	1.173304	0.016061	0.852294	5.113764	4.26147	0.000161	0.55214	-0.117852	0.54831	-0.06492

, , , , T_ок=6Т, Т_га=5Т, h=

T_ок – время окончания расчета,

Т_га – время гармонического анализа

h – шаг расчета.

находим с помощью трассировки аналитической АФЧХ(значения А и В).

Результаты, полученные в программе РИТМ:

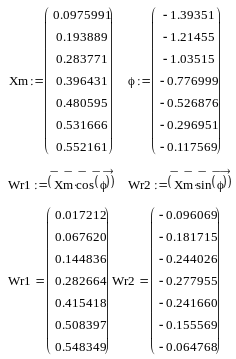
В РИТМе были получены значения для действительной Wr1 и мнимой Wr2 частей АФЧХ. По этим значениям были выставлены 7 точек, которые лежат на аналитической АФЧХ.

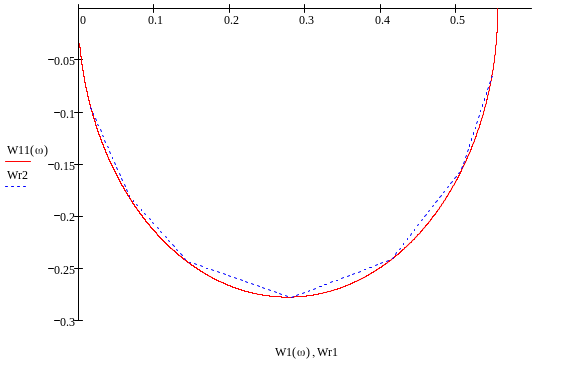
Красный цвет – аналитически построенная АФЧХ.

Синий цвет – экспериментально построенная АФЧХ.

Гармонический анализ.

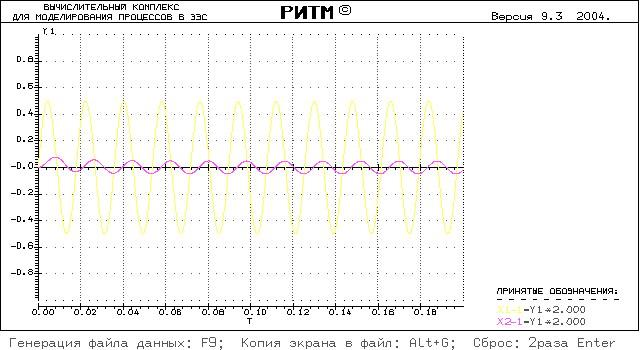
Пункт 8.

Cтруктурная алгоритмическая схема САУ.

Далее преобразуем схему.

1.Объеденяем последовательно соединенные звенья W3 ,W4

2.Переносим вперед через сумматор 6 звено с передаточной функцией W3*W4

3.Объединяем сумматоры 2 и 6. Далее эквивалентируем передаточные функции звеньев W3,W4,W7,W8, объединенных в обратную отрицательную связь, получаем звено W9

4.Эквивалентируем относительно Xуст

Получим эквивалентную передаточную функцию.

5.Эквивалентируем относительно Eo

Получим эквивалентную передаточную функцию.

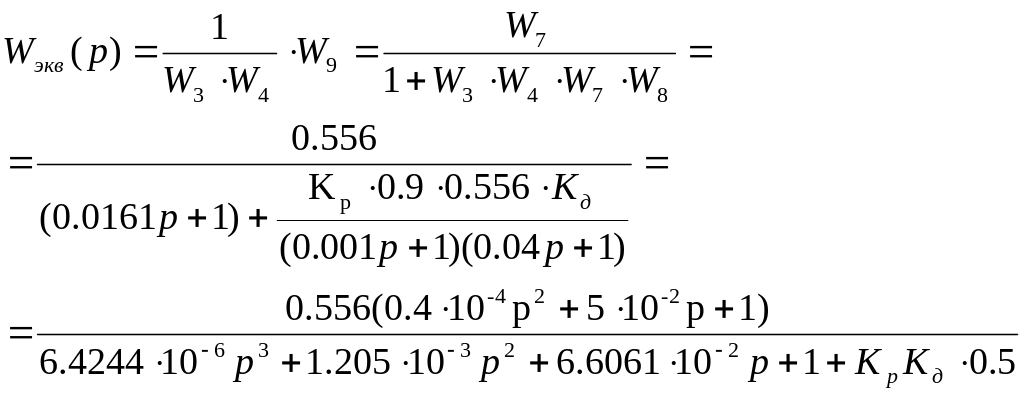
Пункт 9.

Построим область устойчивости системы в плоскости коэффициентов

Из знаменателя эквивалентной передаточной функции:

При замене р на получаем характеристический полином:

,

с коэффициентами

Для определения области устойчивости используем критерий устойчивости Гурвица.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

Т.о. условия устойчивости:

-определитель Гурвица

Для построения границ областей устойчивости используем следующие уравнения

1.

Т.е. = 0

2.

Таким образом, используя следующие уравнения,

строим область устойчивости.

5

4

3

1

2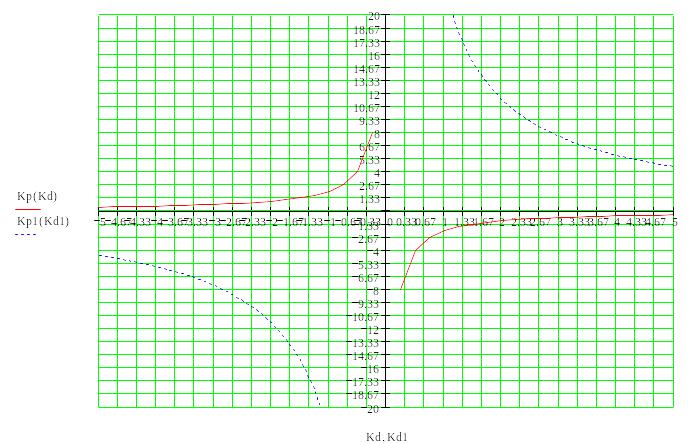

Получаем 5 областей, которые могут быть областями устойчивости. Проверим эти области на устойчивость.

Рассмотрим область 1.

Возьмем

Область 1 не является устойчивой, т.к. не выполняется условие .

Рассмотрим область 2.

Возьмем

Область 2 также не является устойчивой.

Рассмотрим область 3.

Возьмем

Область 3 является устойчивой, т.к. выполняются условия устойчивости, а именно положительность определителя Гурвица и всех его диагональных миноров.

Области 4,5 аналогично областям 1 и 2 не являются устойчивыми.

Преподавателем были выбраны коэффициенты из области устойчивости.

Пункт 10.

Далее, после выбора коэффициентов из области устойчивости, подготовим имитационная модель САУ в программе РИТМ, имеющую следующий вид.

1-генератор кусочно-постоянного сигнала

2-сумматор

коэффициенты сумматора

k = 1, k = -1

3-инерционное звено первого порядка

4- инерционное звено первого порядка

5- генератор кусочно-постоянного сигнала = 1800 В.

6- сумматор

коэффициенты сумматора

k = 1,k = 1

7- инерционное звено первого порядка

8-пропорциональное звено

9-осцилограф

10-табулятор

В результате расчета данной имитационной модели был получен график:

Видно, что при данных настройках системы требуемое условие = 0 в установившемся режиме не выполняется. Внесем некоторые изменения в настройки системы.

Пункт 11.

Обеспечим нулевую величину э.д.с. регулируемого источника.

Для этого изменим значение коэффициента сумматора у Xуст на k=2.

Т.о. через регулируемый источник пройдет нулевой сигнал, и, следовательно, получаем = 0.

Переходный процесс включения системы питания при нулевых начальных условиях будет иметь следующий вид.

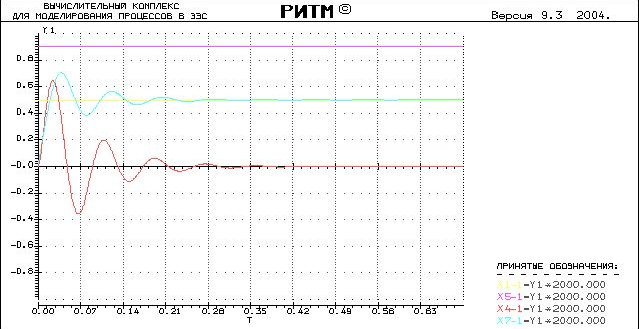
Рассчитаем статизм, перерегулирование и длительность переходного процесса по результатам опыта и теоретически.