4. Расчет емкости 3-х фазной линии выполняется для области

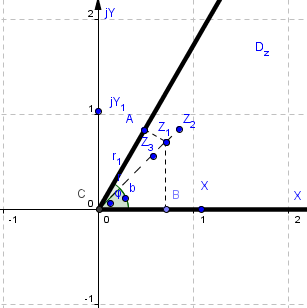
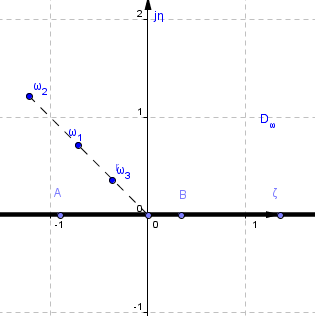Рис.14. Расположение проводов в области Рис.15. Расположение проводов в

Из инвариантности емкости при конформном отображении области расчета следует:

усреднённое значение собственного потенциального коэффициента провода.

- усреднённое значение взаимного потенциального коэффициента провода.

4.1. Расчёт производим в области , поэтому переводим координаты осей проводов из в :

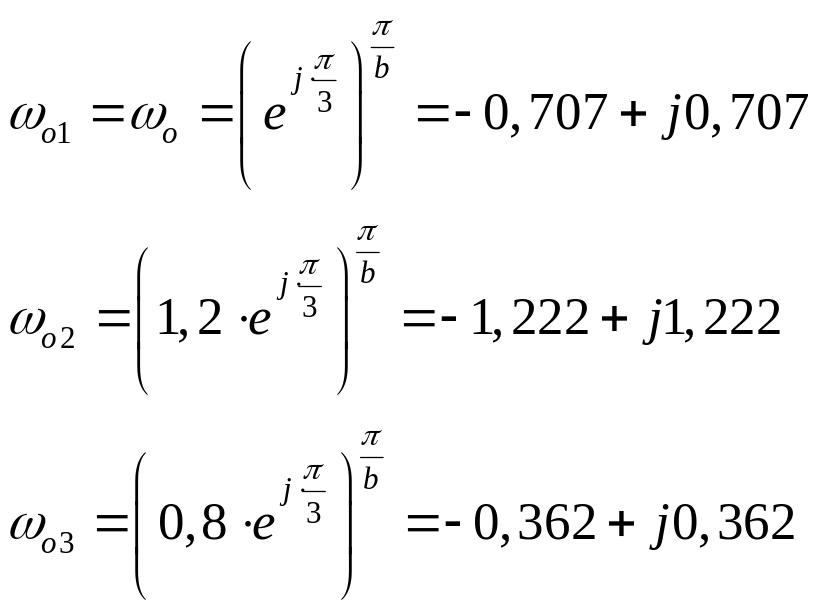4.2.Пересчитаем радиусы проводов из области в :

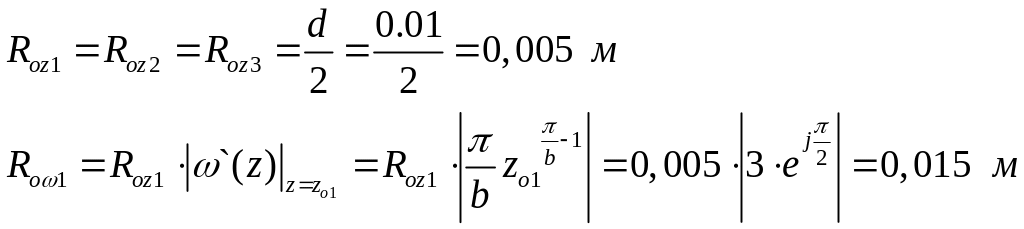
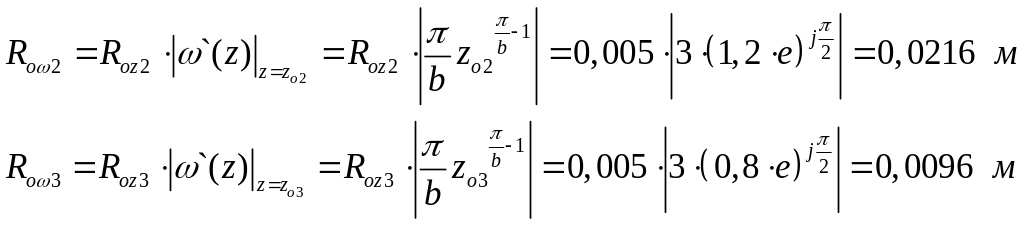
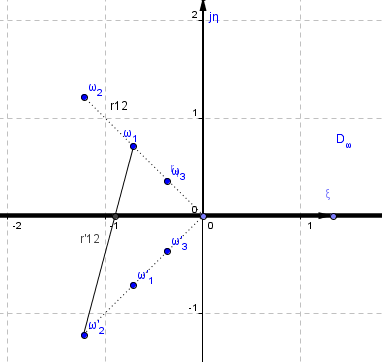_{Рис.16. Расположение проводов полученных методом зеркальных отображений.}

4.3.Расчитаем собственные и взаимные потенциальные коэффициенты

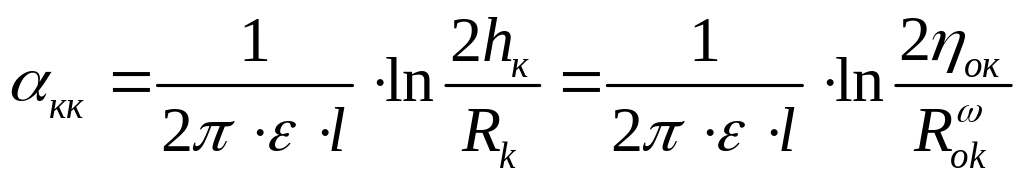
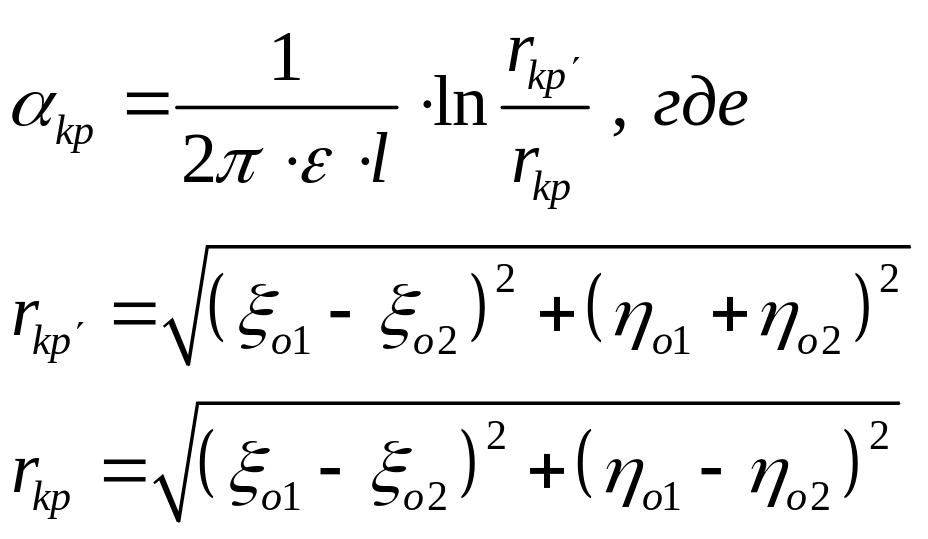
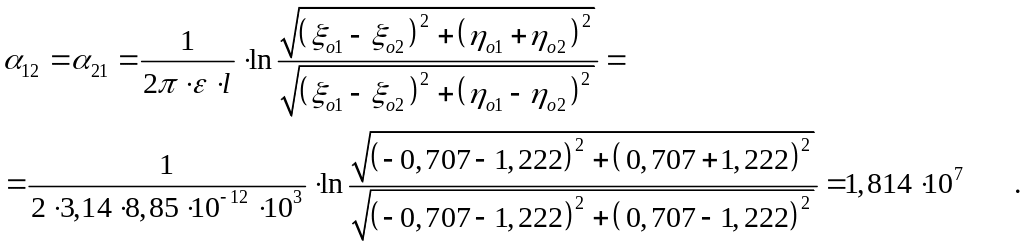
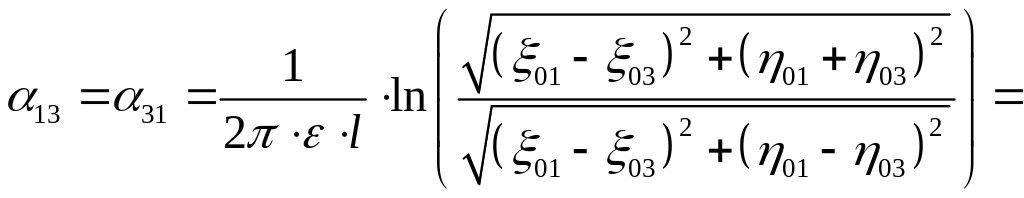
По найденным значениям коэффициентов вычислим средние значения:

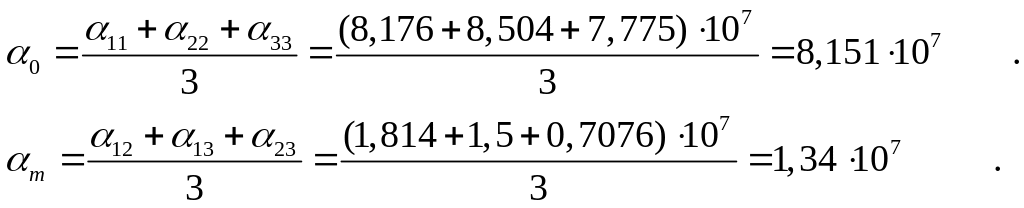
Найдём ёмкость :

5. Расчёт значения ёмкости с без учёта влияния земли

Сравнение полученного значения ёмкости C с приближённым значением, рассчитанным без учёта влияния земли.

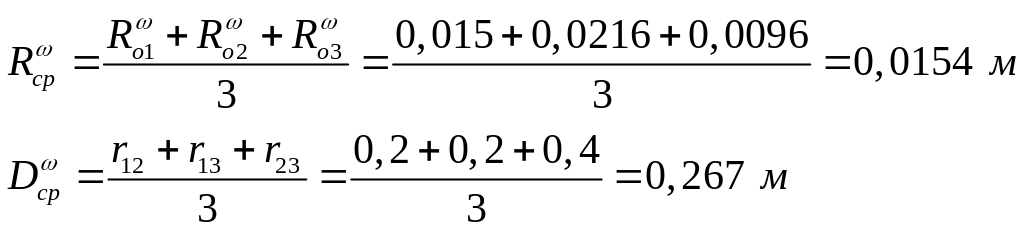
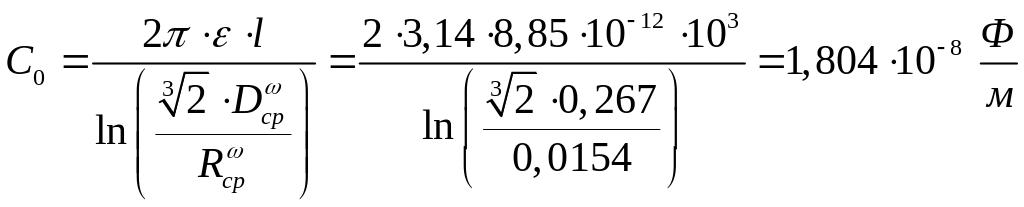
5.1. Оценка погрешности расчёта ёмкости линии на фазу в пренебрежении влиянием земли Расчётное выражение для погрешности имеет вид:

Как видно, в данном случае пренебрежение влиянием земли приводит к достаточно большой погрешности для ёмкости линии на фазу.

3. Построение картины поля и численный расчет

ПЛОСКОПАРАЛЛЕЛЬНОГО МАГНИТНОГО ПОЛЯ

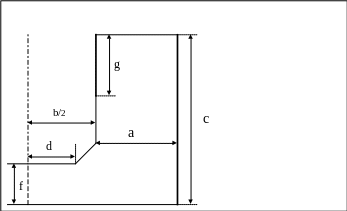
Листы из ферромагнитного вещества образуют сердечник толщиной 0,02м (см. рисунок). На среднем стержне сердечника расположена обмотка с числом витков w₁ =100, на его крайних стержнях расположены обмотки с числом витков w₂ =200. Постоянный ток средней обмотки равен 1А, токи крайних обмоток равны нулю.

1.Постройте приближенную картину плоскопараллельного магнитного поля в воздушной области, ограниченной внутренним контуром листов, считая магнитную проницаемость вещества сердечника бесконечной. Обмотку среднего стержня представьте в виде бесконечно тонкого слоя тока, по высоте которого ток расположен равномерно.

2. Рассчитайте индуктивность обмотки среднего стержня L и взаимную индуктивность М между обмотками среднего и правого стержней, используя построенную картину магнитного поля.

3. Рассчитайте методом сеток векторный магнитный потенциал в воздушной области, ограниченной внутренним контуром листов, найдите индуктивность обмотки среднего стержня L и сопоставьте ее с полученной на основе приближенной картины поля. Расчет выполнить, принимая толщину обмотки среднего стержня равной: а). 2см, б). 4см.

4. По результатам расчета векторного магнитного потенциала постройте семейство линий напряженности магнитного поля.

Размеры магнитной системы

а, см	b, см	c, см	d, см	f, см	g, см
8	12	16	4	4	4

1. Построение приближенной картины магнитного поля в воздушной области, ограниченной внутренним контуром листов, принимая допущения о том, что магнитная проницаемость вещества сердечника бесконечно велика, и что магнитное поле является плоскопараллельным. Обмотку стержня 1 будем представлять в виде бесконечно тонкого охватывающего стержень слоя тока, по высоте которого ток распределен равномерно.

Для построения картины магнитного поля, включающий в себя линии напряженности и линии постоянных значений скалярного магнитного потенциала, следует задать граничные условия для скалярного магнитного потенциала на линии . Поскольку обмотка стержня 1 представлена в виде бесконечного тонкого слоя с постоянной линейной плотностью тока, то скалярный магнитный потенциал изменяется вдоль линии по линейному закону, причем разность потенциалов между точками и равна А. Потенциал в точке зада­ем равным нулю. Так как магнитная проницаемость материала сердечника при­нята бесконечно большой, то скалярный потенциал на линии сохраняется постоянным и равным нулю. По той же причине потенциал будет постоянным и равным 100 А на линии . Линия является линией симметрии; нормаль­ная к ней составляющая напряженности магнитного поля равна нулю, и поэтому на ней .

При построении картины поля следует соблюдать следующие правила: а) ли­нии напряженности поля и линии постоянного потенциала должны пересекать­ся под прямым углом, б) линии напряженности поля должны подходить под прямым углом к поверхностям, на которых потенциал постоянный, в) ячейки сетки, образованные линиями напряженности поля и линиями постоянного по­тенциала, должны быть подобными. Примем изменение потенциала при переходе от любой линии к соседней равным 25 А. В этом случае следует изобразить всего три линии, на которых по­тенциал равен 25 А, 50 А и 75 А. Необходимо отметить точки токового слоя, в ко­торых потенциал принимает эти значения, и проводить линии, начиная с этих точек. Так как линейная плотность тока постоянна, то эти точки распределены вдоль линии равномерно. Определив ориентировочно вид этих линий, пере­ходим к изображению линий напряженности магнитного поля, стараясь выпол­нить правила построения картины поля. Обычно линии напряженности поля проводят так, чтобы ячейки были квадратными или близкими к ним, т.е. чтобы отношение (рис.17.) было близким к единице. 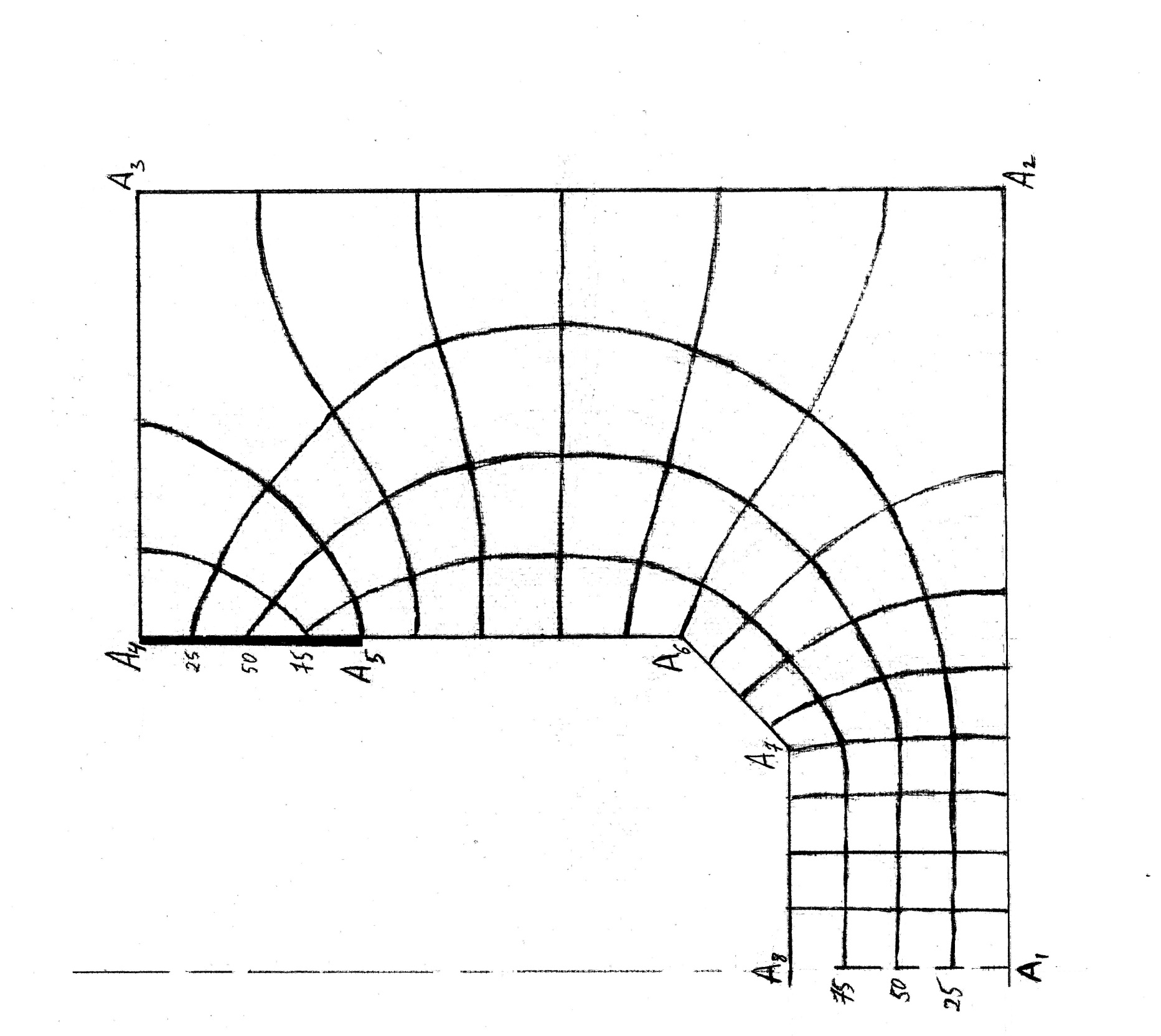Рис.17.Приближенная картина плоскопараллельного магнитного поля.

После этого следует скорректировать положение линий постоянного потен­циала, затем — положение линий напряженности поля и т. д. Эту процедуру сле­дует выполнять до тех пор, пока картина поля не будет удовлетворять требуе­мым правилам. В итоге получаем картину поля, в которой линии напряженности подразделяют всю область на трубки постоянных значений по­тока. Заметим, что линии напряженности поля подходят к линии под углом, не равным 90°, так как на этой линии распределен слой тока.