Учебно-методическое пособие

Множества. Задание множеств. Операции над

Множествами.

Элементы теории множеств: Множества. Операции над множествами

Сведения из теории

Понятия множества не определяется, а лишь поясняется на примерах. Можно говорить о множестве стульев в аудитории, о множестве деревьев в парке, о множестве машин на улицах города, о множестве людей на планете, о множестве людей в Европе, о множестве климатических зон, о множестве точек на прямой, о множестве натуральных чисел и т.п.

–

Объекты, из которых состоит множество, называются его элементами.

–

Если в множестве имеется элемент 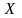, то пишут или и говорят, что элемент входит в множество (принадлежит множеству , содержится в множестве ) или что множество содержит элемент .

Если элемент в множество не входит, то пишут или .

Множества бывают конечные; бесконечные и пустые.

Множество называется конечным, если в нем содержится конечное число элементов.

Например, множество рек в Карелии конечно, множество пустынь на Земле конечно, множество деревьев в тайге конечно.

Множество называется пустым, если оно не содержит ни одного элемента.

Например, множество гор в Карелии, высота которых более 5000 м., пустое.

Множество, которое не является ни конечным, ни пустым, называется бесконечным.

Например, множество натуральных чисел бесконечно, множество точек на окружности бесконечно и т. д.

Задать множество, это значит указать необходимое и достаточное условие попадания элемента в данное множество.

Другими словами, указать набор признаков, по которым для любого объекта мы можем сказать, является этот объект элементом данного множества или не является.

Если множество конечное и все его элементы известны, то говорят, что множество задано перечислением своих элементов.

При этом, если множество состоит из элементов , , , то пишут:

.

Если множество бесконечное или конечное, но мы не знаем его элементы, то задание множества осуществляется с помощью указания характеристического свойства элементов этого множества.

Характеристическим свойством элементов данного множества называется необходимое и достаточное условие попадания объекта в данное множество, выраженное словесно или с помощью математических символов.

Например: читаем: множество из таких элементов , которые являются вещественными числами, большими или равными 1. Характеристическое свойство элементов, входящих в множество _, состоит из трёх положений:

1. объект должен быть числом,

2. объект должен быть вещественным числом,

3. объект должен быть вещественным числом, большим или равным единицы.

Элемент , который фигурирует в записи этого множества, называют текущим элементом множества .

Пустые множества обозначают символом .

При задании множества учитываются следующие договорённости:

1. При записи множества порядок символов, обозначающих элемент данного множества не существенен. Т. е., если множество состоит из трёх элементов, обозначенных символами , , , то мы можем записать , а можем записать . Заметим, всего видов записи множества , состоящего из трёх элементов ; ; шесть штук.

2. Один и тот же символ нельзя употреблять для обозначения двух разных элементов. Т. е., если один из элементов множества обозначен символом а, то второй элемент символом а обозначить нельзя. Нужно применить другой символ, например, .

3. Два разных символа нельзя употреблять для обозначения одного и того же элемента. Заметим, ограничения 2 и 3 позволяют сделать вывод, что если мы имеем запись , то это значит, что в множестве имеется в точности три различных элемента, а если мы имеем запись , то это не запись множества.

4. Элемент из множества можно взять столько раз, сколько это нужно для рассуждений.

Это означает, что вынимая из множества элемент а, мы не лишаемся его в множестве. Он там по-прежнему присутствует. И мы его можем вынимать столько раз, сколько нам требуется для рассуждений.

Пусть даны множества и . При этом мы не указываем, какие это множества – конечные, бесконечные или пустые. Если каждый элемент множества является элементом множества , т. е.

то говорят, что множество есть подмножество множества , и пишут .

По определению и . Другими словами, у непустого множества всегда есть, по крайней мере, два подмножества и . Эти подмножества называются несобственными подмножествами (тривиальными). Все остальные подмножества множества называются собственными подмножествами.

Если множество конечное и состоит из элементов, то говорят, что множество имеет длину и пишут .

Если , то подмножеств у него .

Например, если , т. е. , то оно имеет подмножеств: , , , , , , , . Других подмножеств у множества М нет.

Пусть даны множества и .

Если и , то множества и называются равными. Другими словами, множества и называются равными, если выполняются следующие условия:

2. .

При этом пишут .

С помощью множеств и можно образовать другие множества.

Объединение множеств и называется такое множество , которое состоит из всех элементов множества и всех элементов множества и только из этих элементов.

Объединение множеств и обозначается символом .

Итак, .

Например, если , , то .

Пересечением множеств и называется такое множество , которое состоит из элементов, принадлежащих одновременно и множеству и множеству , и только из таких элементов.

Пересечение множеств и обозначают символом .

Итак, .

Например, если и , то .

Разностью множеств и называется такое множество , которое состоит из элементов множества , не входящих в множество , и только из этих элементов.

Разность множеств и обозначают символом .

Итак, .

Например, если , , то , а .

В частности, если , то называют дополнением множества до множества и обозночают символом _.

Например, если , , то .

Чтобы наглядно изобразить множества и их взаимосвязи, часто рисуют круги, находящиеся в аналогичных взаимосвязях. Каждый круг на рисунке изображает некоторое множество. При этом точки круга не ассоциируют с элементами множества. Т. е. круг может соответствовать как конечному множеству, так и бесконечному, так и пустому. Это изображение аналогично представлению множества в виде мешка, в котором находятся элементы множества. Мешок может содержать конечное число элементов, бесконечное число элементов, быть пустым.

Круги, с помощью которых наглядно изображаются множества, называются кругами Эйлера-Венна, а способ изображения множеств с помощью кругов называется диаграммами Эйлера-Венна.

Рассмотрим некоторые диаграммы Эйлера-Венна:

рис. 1 рис. 2 рис. 3 рис. 4

Каждая диаграмма соответствует определенной взаимосвязи множеств и :

1. (рис. 1)

2. (рис. 2 – заштрихованная часть),

3. (рис. 3 – заштрихованная часть),

4. (рис. 4 – заштрихованная часть).

Нередко бывает так, что рассматривают только подмножества одного и того же множества . Такое множество называют универсальным множеством. Понятие универсального множества относительно. Для каждой задачи оно свое.