
- •Оптимизация. Критерии оптимальности; целевая функция. Классификация. Модели оптимизационных задач. Примеры.
- •Решение краевых задач для обыкновенных дифференциальных уравнений и систем. Основные положения.
- •Метод стрельбы. Схемы дихотомии и секущих.
- •Метод стрельбы для линейной краевой задачи.
- •Метод конечных разностей, или метод сеток.
- •Полуаналитические методы решения краевой задачи. Метод коллокации.
- •Полуаналитические методы решения краевой задачи. Метод Галеркина.
- •Разностные схемы для уравнений в частных производных. Основные понятия.
- •Сходимость, аппроксимация и устойчивость разностных схем
- •Разностные схемы для уравнений параболического типа. Решение задачи Коши.
- •Устойчивость двухслойных разностных схем для уравнений параболического типа
- •Построение разностной аппроксимации для уравнения Пуассона.
- •Различные краевые задачи и аппроксимация граничных условий.
- •Построение разностной схемы в случае задачи Дирихле для уравнения Пуассона.
- •Метод матричной прогонки. Итерационный метод решения разностной схемы для задачи Дирихле.
- •Итерационный метод решения разностной схемы для задачи Дирихле
- •Разностные схемы для уравнений гиперболического типа. Решение задачи Коши Разностные схемы для уравнений гиперболического типа
- •Решение задачи Коши
- •Разностные схемы для уравнений гиперболического типа. Решение смешанной задачи.
- •Общие понятия метода конечных элементов.
- •Дискретизация области и нумерация узлов.
- •Линейные интерполяционные полиномы.
- •Одномерный симплекс-элемент.
- •Двумерный симплекс-элемент.
- •Местная система координат.
- •Двумерные l-координаты.
- •Объединение элементов в ансамбль.
- •Вывод уравнений для элементов с помощью метода Галеркина.
- •Пример расчета одномерного температурного поля в однородном стержне.
Построение разностной аппроксимации для уравнения Пуассона.
Рассмотрим в некоторой области D с границей Г уравнение Пуассона
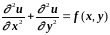 .
(3.25)
.
(3.25)
Выберем прямоугольную сетку по правилу
 .
.
К сеточной области
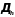 отнесем все узлы, принадлежащие области
отнесем все узлы, принадлежащие области
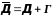 (рис. 5).
(рис. 5).
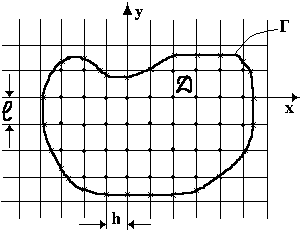
Рис. 5. К построению разностной аппроксимации
Возьмем пятиточечный шаблон

Пользуясь
расположением точек в этом шаблоне,
разобьем узлы
области на две категории: внутренние и
граничные. Узел
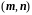 будем считать внутренним,
если он сам и четыре соседних точки
шаблона принадлежат области
(эти узлы обозначены символом ).
Обозначим множество внутренних узлов
через
будем считать внутренним,
если он сам и четыре соседних точки
шаблона принадлежат области
(эти узлы обозначены символом ).
Обозначим множество внутренних узлов
через
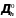 .
Остальные узлы назовем граничными
(помечены
.
Остальные узлы назовем граничными
(помечены
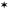 )
и их множество обозначим через
)
и их множество обозначим через
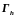 .
.
Таким образом,
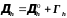 .
.
Очевидно, что разбиение узлов из на внутренние и граничные зависит от выбранного шаблона.
Пусть узел
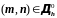 .
Замену дифференциального уравнения
(3.25) разностным будем осуществлять
только во внутренних узлах.
.
Замену дифференциального уравнения
(3.25) разностным будем осуществлять
только во внутренних узлах.
Имеем
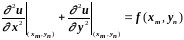 .
(3.26)
.
(3.26)
Воспользовавшись аппроксимацией вторых производных, получим

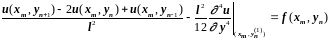 ,
,
(3.27)
,
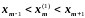 ,
,
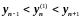 .
.
Пусть
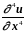 и
и
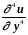 ограничены
по абсолютной величине в
ограничены
по абсолютной величине в
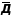 .
Тогда в формуле (3.27) при достаточно малых
h
и l
можно пренебречь членами, содержащими
в качестве множителей
.
Тогда в формуле (3.27) при достаточно малых
h
и l
можно пренебречь членами, содержащими
в качестве множителей
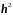 и
и
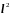 ,
и мы получим искомое разностное уравнение
,
и мы получим искомое разностное уравнение
 ,
(3.28)
,
(3.28)
где
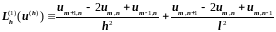 ,
,
,
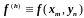 .
.
В силу определения невязки уравнения можно получить
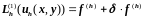 ,
(3.29)
,
(3.29)
где
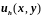 – точное решение в узлах,
– точное решение в узлах,
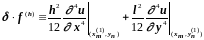 ,
.
(3.30)
,
.
(3.30)
При сделанных
предположениях относительно
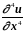 и
и
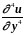 ,
как видно из (3.30), имеет место оценка
,
как видно из (3.30), имеет место оценка
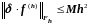 .
(3.31)
.
(3.31)
Здесь М
– постоянная, не зависит от
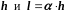 .
.
Оценка (3.31) означает,
что разностное уравнение (3.28) аппроксимирует
уравнение (3.25) на решение u(x,
y)
с погрешностью порядка
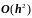 .
.
Различные краевые задачи и аппроксимация граничных условий.
К уравнениям эллиптического типа, в частности, к уравнению Пуассона (3.25), на границе Г области D присоединяются граничные условия трех видов:
граничные условия 1-го рода:
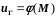 ;
(3.32)
;
(3.32)
граничные условия 2-го рода:
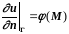 ,
(3.33)
,
(3.33)
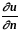 – производная по
внешней нормали;
– производная по
внешней нормали;
граничные условия 3-го рода:
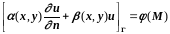 ,
(3.34)
,
(3.34)
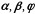 – известные
функции.
– известные
функции.
Если требуется
определить функцию
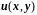 ,
которая в области D
удовлетворяет уравнению (3.25), а на границе
Г
– одному из краевых условий, то говорят,
что поставлена граничная задача для
эллиптического уравнения.
,
которая в области D
удовлетворяет уравнению (3.25), а на границе
Г
– одному из краевых условий, то говорят,
что поставлена граничная задача для
эллиптического уравнения.
Задача (3.25), (3.32) называется задачей Дирихле,
задача (3.25), (3.33) – задачей Неймана,
а задача (3.25), (3.34) – смешанной граничной задачей.
Рассмотрим, как можно заменить граничные условия первого рода разностными условиями (рис. 6). Отметим, что граничные условия заменяются условиями на множестве граничных узлов .
Пусть
– некоторый узел из
;
обозначим его буквой В;
 – внутренний узел, ближайший к В
по направлению
x;
обозначим его буквой А.
Буквой М
обозначим точку контура Г,
ближайшую к В
по направлению x.
– внутренний узел, ближайший к В
по направлению
x;
обозначим его буквой А.
Буквой М
обозначим точку контура Г,
ближайшую к В
по направлению x.
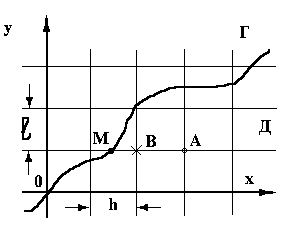
Рис. 6. Замена граничных условий первого рода разностными условиями
Координаты этих точек такие:
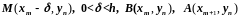 .
.
По условию (3.32)
имеем
 .
.
Значит, можно положить
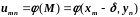 (3.35)
(3.35)
для узлов .
Найдем погрешность формулы (3.35).
Имеем
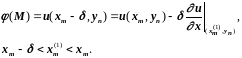
Значит,

Отсюда следует,
что погрешность формулы (3.35) будет иметь
первый порядок относительно h
в предположении,
что
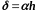 .
Если точки М
и В
совпадают, то формула (3.35) будет точной.
.
Если точки М
и В
совпадают, то формула (3.35) будет точной.
Точность вычисления
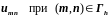 можно повысить, если воспользоваться
еще значением
в точке А.
можно повысить, если воспользоваться
еще значением
в точке А.
Имеем:
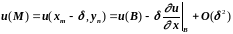 ,
(3.36)
,
(3.36)
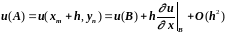 .
(3.37)
.
(3.37)
Исключив из (3.36)
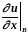 с помощью (3.37), получим
с помощью (3.37), получим
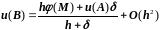 .
.
Отбросив здесь
величину
,
найдем разностное граничное условие,
аппроксимирующее граничное условие
(3.32) в узле
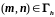 с погрешностью
:
с погрешностью
: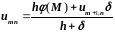 .
(3.38)
.
(3.38)
Обратимся теперь к замене граничного условия 2-го рода разностным уравнением (рис. 7).
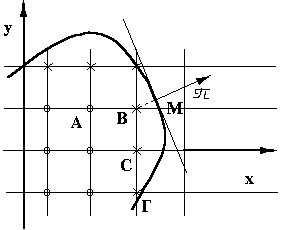
Рис. 7. Замена граничных условий второго рода разностными условиями
Пусть В
– граничный узел с координатами
 ,
М
– ближайшая к В
точка контура Г,
А
– внутренний узел с координатами
,
М
– ближайшая к В
точка контура Г,
А
– внутренний узел с координатами
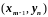 ,
С
– граничный узел с координатами
,
С
– граничный узел с координатами
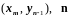 – внешняя нормаль к Г
в точке М.
Обозначим угол между
– внешняя нормаль к Г
в точке М.
Обозначим угол между
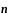 и осью Ox
через ,
между
и осью Oy
– через .
Очевидно, что
и осью Ox
через ,
между
и осью Oy
– через .
Очевидно, что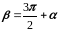 .
.
По определению имеем
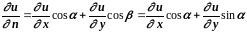 .
.
Предположим, что
в точке В
направление нормали такое же, как и в
точке М.
Поскольку расстояние между В
и М
есть величина порядка
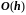 ,
то это предположение связано с внесением
погрешности того же порядка
.
Значит,
,
то это предположение связано с внесением
погрешности того же порядка
.
Значит,
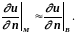
Поэтому окончательно получим
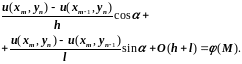
Используя приблизительные сеточные значения, найдем
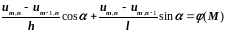 .
(3.39)
.
(3.39)
Эта формула является
разностной аппроксимацией в узле
граничного условия второго рода с
погрешностью
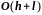 .
.
Выражения вида (3.39) должны быть записаны для всех граничных узлов , после чего будут получены разностные граничные условия, аппроксимирующие граничные условия (3.33). Процедура замены граничных условий разностными может оказаться весьма громоздкой и сложной, особенно если контур Г имеет непростую форму. Замена граничных условий третьего рода может быть осуществлена с помощью формул вида (3.35), (3.37), (3.38).
