26. Вывод уравнений для элементов с помощью метода Галеркина.

Если исходить из дифференциального уравнения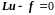

и приближенное решение искать в виде , то для него будем иметь

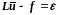, где  – ошибка, или невязка, поскольку решение 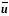− приближенное.

Необходимо сделать  малой величиной.

В методе Галеркина это достигается с помощью соотношений ортогональности

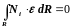
для каждой из базисных функций N_i.

Это равенство означает, что базисные функции должны быть ортогональны ошибке по области R.

Применение метода Галеркина в сочетании с МКЭ приводит к уравнениям

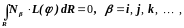(3.106)

где  искомая величина, которая аппроксимируется соотношением

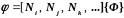, (3.107)

а L() − левая часть дифференциального уравнения L() = 0, которое необходимо решить.

27. Пример расчета одномерного температурного поля в однородном стержне.

Пусть имеется стержень длиной L и площадью поперечного сечения S. Один конец стержня закреплен и к нему подводится тепловой поток q заданной интенсивности (рис. 19).

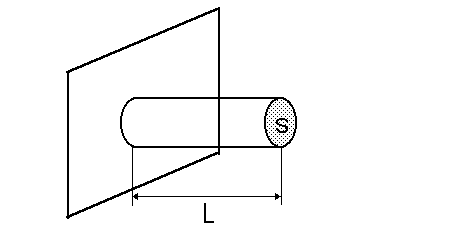
Рис. 19. Иллюстрация к примеру 3.5.10

На свободном конце стержня происходит конвективный теплообмен с внешней средой. Коэффициент теплообмена – , а температура окружающей среды − Т₀. Вдоль боковой поверхности стержень теплоизолирован.

Температурное поле в стержне описывается уравнением теплопроводности

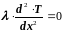. (3.108)

Краевые условия следующие:

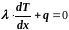при х=0, (3.109^а)

при x=L. (3.109^б)

Здесь  − коэффициент теплопроводности,  − коэффициент теплопередачи.

Разобьем стержень на два конечных элемента и обозначим длину каждого из них через L^(e), е=1, 2.

Применив метод Галеркина к уравнению (3.108), получим

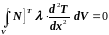, (3.110)

где [N]^T − вектор-столбец, полученный транспонированием строки [N] из функций формы одномерного симплекс-элемента (3.81).

Подставим в (3.110) формулу дифференцирования произведения:

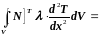
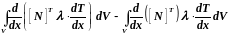. (3.111)

Интерполяционная функция Т является кусочно-линейной, поэтому интегралы в (3.111) можно представить суммой соответствующих интегралов для отдельных элементов. Так, второй интеграл в (3.111) можно представить в виде

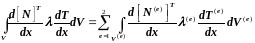. (3.112)

Вычислим в (3.112) интегралы, относящиеся к отдельным элементам:

, (3.113)

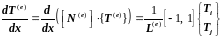. (3.114)

Теперь

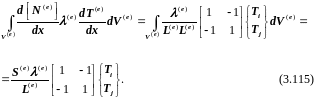
Первый интеграл в (3.111) на основании теоремы Остроградского-Гаусса преобразуется к виду

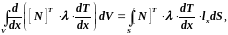(3.116)

где 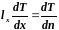, n − внешняя нормаль к рассматриваемой поверхности.

С учетом краевого условия (3.109^а) в точке х=0 для первого элемента интеграл (3.116) примет вид

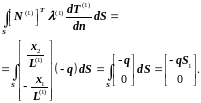(3.117)

С учетом краевого условия (3.109^б) в точке х=L для второго элемента интеграл (3.111) запишется так:

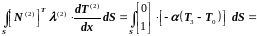
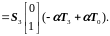(3.118)

Здесь 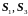− левое и правое сечения стержня.

Учитывая, что под интегралом (3.112), (3.117), (3.118) стоят матрицы, найдем, что при суммировании должны складываться строки этих матриц, отвечающие одинаковым узлам. Просуммировав выражения вида (3.115) для первого и второго элементов и выражения (3.117), (3.118) и приравняв сумму нулю, получим систему уравнений

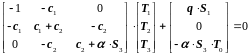. (3.119)

Здесь , .

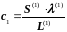Система (3.119) и определяет узловые значения .

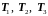Завершающим этапом МКЭ является решение системы линейных алгебраических уравнений.

67