1. Оптимизация. Критерии оптимальности; целевая функция. Классификация. Модели оптимизационных задач. Примеры.

2. Решение краевых задач для обыкновенных дифференциальных уравнений и систем. Основные положения.

3. Метод стрельбы. Схемы дихотомии и секущих.

4. Метод стрельбы для линейной краевой задачи.

5. Метод конечных разностей, или метод сеток.

6. Полуаналитические методы решения краевой задачи. Метод коллокации.

7. Полуаналитические методы решения краевой задачи. Метод Галеркина.

8. Разностные схемы для уравнений в частных производных. Основные понятия.

9. Сходимость, аппроксимация и устойчивость разностных схем

10. Разностные схемы для уравнений параболического типа. Решение задачи Коши.

11. Устойчивость двухслойных разностных схем для уравнений параболического типа.

12. Построение разностной аппроксимации для уравнения Пуассона.

13. Различные краевые задачи и аппроксимация граничных условий.

14. Построение разностной схемы в случае задачи Дирихле для уравнения Пуассона.

15. Метод матричной прогонки. Итерационный метод решения разностной схемы для задачи Дирихле.

16. Разностные схемы для уравнений гиперболического типа. Решение задачи Коши.

17. Разностные схемы для уравнений гиперболического типа. Решение смешанной задачи.

18. Общие понятия метода конечных элементов.

19. Дискретизация области и нумерация узлов.

20. Линейные интерполяционные полиномы.

21. Одномерный симплекс-элемент.

22. Двумерный симплекс-элемент.

23. Местная система координат.

24. Двумерные L-координаты.

25. Объединение элементов в ансамбль.

26. Вывод уравнений для элементов с помощью метода Галеркина.

27. Пример расчета одномерного температурного поля в однородном стержне.

1. Оптимизация. Критерии оптимальности; целевая функция. Классификация. Модели оптимизационных задач. Примеры.

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Критерий оптимальности — характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может быть установлено несколько критериев оптимальности.

Функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.

В широком смысле целевая функция есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим. 

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

• Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

• Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Модели, способные воспроизводить только качественную сторону изучаемого процесса, называются качественными. Более сложными моделями являются количественные, или математические, модели, с помощью которых можно предсказывать конкретные численные значения характеристик явления. Так, например, модель погоды, основанная на народных приметах, будет качественной. Модели же, используемые в гидрометцентрах и позволяющие предсказывать численные значения характеристик погоды (температура, скорость ветра и т.п.), относятся к количественным моделям. Математическая модель – это совокупность уравнений (алгебраических, дифференциальных, интегральных), описывающих процессы, происходящие в моделируемом явлении. Каждое такое уравнение само по себе есть модель процесса более низкого уровня. Модели же сложных явлений часто строятся, как из кирпичиков, из моделей более простых. Результатом математического моделирования являются формулы (если удается получить аналитическое решение уравнений модели), которые позволяют рассчитать характеристики моделируемого процесса или таблицы значений этих характеристик (если аналитическое решение получить не удается, либо оно не удобно). Чаще всего встречается именно последний случай, когда решение можно получить лишь в виде таблицы с помощью каких-либо вычислительных процедур. Такого рода модели носят специальное название  численных моделей. Специфика этих моделей состоит в том, что они позволяют получить принципиально приближенное решение, что связано с дискретностью вычислительных устройств, ограниченным объемом памяти, конечным быстродействием и т.п.

2. Решение краевых задач для обыкновенных дифференциальных уравнений и систем. Основные положения.

Краевая задача – это задача отыскания частного решения системы

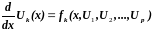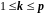, (2.1)

на отрезке 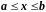, причем дополнительные условия налагаются на значения функций более чем в одной точке этого отрезка.

Заметим, что дифференциальное уравнение порядка р

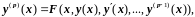(2.3)

где 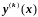− производная порядка

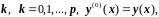
может быть сведено к системе дифференциальных уравнений вида (2.1) заменой переменных

(2.4)

Действительно, по замене (2.4)

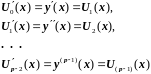
и уравнение (2.3) сведется к следующей системе вида (2.1):

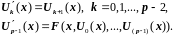
Здесь последнее уравнение получено подстановкой (2.4) в (2.3).

Заметим, что общая краевая задача (2.1) может:

• не иметь решений;

• иметь единственное решение;

• иметь несколько и даже бесконечно много решений.

Рассмотрим более подробно важный частный случай, когда дифференциальное уравнение и краевые условия линейны. Такая краевая задача называется линейной краевой задачей.

Линейное дифференциальное уравнение n-го порядка сокращенно можно записать в виде

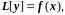(2.6)

Где

причем обычно предполагается, что 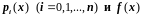− известные непрерывные функции на данном отрезке .

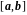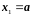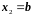
Для простоты будем предполагать, что в краевые условия входят две абсциссы и 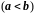− концы отрезка . Такие краевые условия называются двухточечными. Краевые условия называются линейными, если они имеют вид

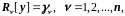(2.7)

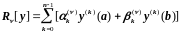Где и 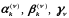− заданные постоянные, причем

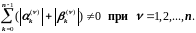
Например, краевые условия, приведенные в предыдущих примерах, линейны.

Линейными краевыми условиями являются также условия периодичности, которые в случае дифференциального уравнения второго порядка имеют вид

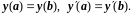
Линейная краевая задача называется однородной, если:

• во-первых, 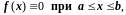то есть дифференциальное уравнение (2.6) однородно, и,

• во-вторых, 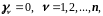то есть имеют место однородные краевые условия.

В противном случае краевая задача (2.6)-(2.7) называется неоднородной.