2.2.5 Интегрирование простейших иррациональных функций

В данном пункте рассмотрим интегралы вида: , которые находятся

подстановкой , , (Правило 5)

При интегрировании иррациональных функций с помощью подстановки необходимо

избавиться от иррациональности (корня).

86

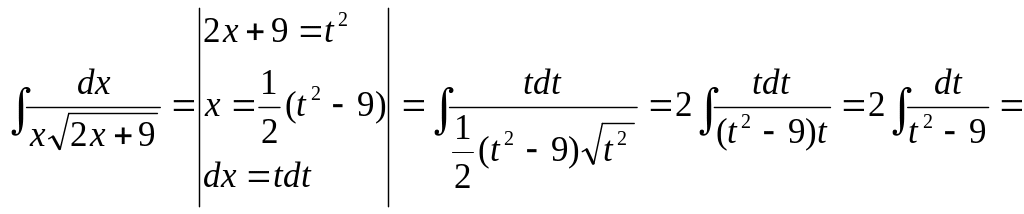
87

Замечание. Этот способ интегрирования применяется и в том случае, когда под корнем

стоит трансцендентная функция.

88

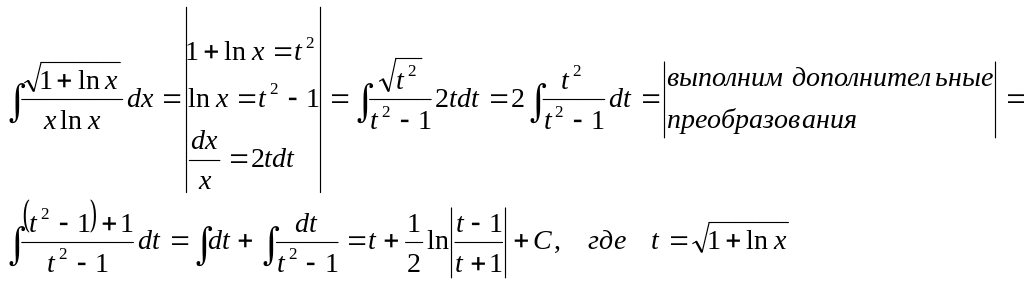
89

Выполните самостоятельно

90 91

92 93

94

2.2.6 Применение преобразований пф при интегрировании

Иногда, прежде чем найти интеграл необходимо выполнить преобразования ПФ (применить формулы элементарной математики, почленное деление числителя ПФ на знаменатель).

95 ;

Обозначим данный интеграл I, тогда

96

Выполните самостоятельно

97 98 99 100

ВНИМАНИЕ Если вы хорошо овладели интегрированием методом подстановки, то

должны уметь применять этот метод и в нестандартных интегралах.

101

Способ 1

Способ 2

Способ 3

, далее как способом 2.

На этом примере вы убедились, что один и тот же метод можно применять

различными способами. Многое зависит от вашего уровня понимания самого процесса интегрирования.

Рассмотрите еще один пример

102

Выполните самостоятельно

103 Указание

104 Указание

105 Указание помножьте числитель и знаменатель на 2 и примените формулу

106

107 Указание

108

109* 110*

2.3 Метод интегрирования по частям

Если подынтегральная функция (ПФ) представлена как произведение алгебраической функции на трансцендентную функцию, то в этом случае применяется метод интегрирования по частям.

Например: , , , и т.д.

Пусть и - функции, имеющие непрерывные производные. Тогда

(1)

Найдем интегралы от левой и правой части равенства. (1)

Применим свойства 2.3 и 2.5 получим:

Из полученного равенства выразим

(2)

Полученная формула (2) называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла к вычислению интеграла , который может оказаться существенно более простым, чем исходный. При этом следует иметь в виду, что к u следует относить множители, которые упрощаются при дифференцировании.

Например, если под знаком интеграла стоит произведение многочлена на тригонометрическую или показательную функцию, то к u следует отнести многочлен, а оставшееся выражение к dv.

Если ПФ содержит сомножителем логарифмическую или обратную тригонометрическую функции, то их следует принимать за u, так как в результате дифференцирования эти функции упрощаются.

Укажем некоторые типы интегралов, которые удобно вычислять по частям

Т а б л и ц а 1

Тип интеграла	u	dv
1
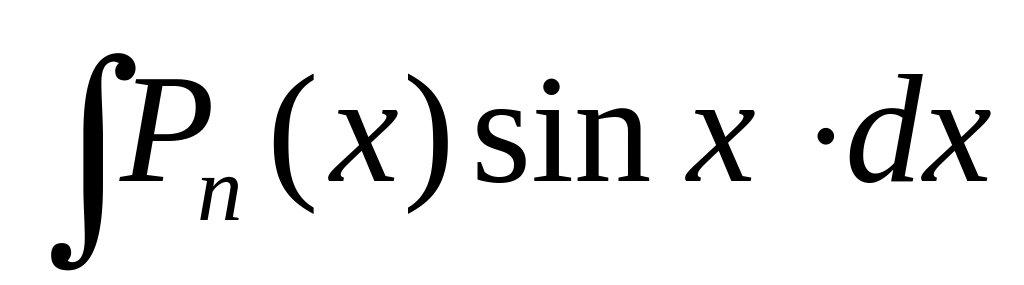
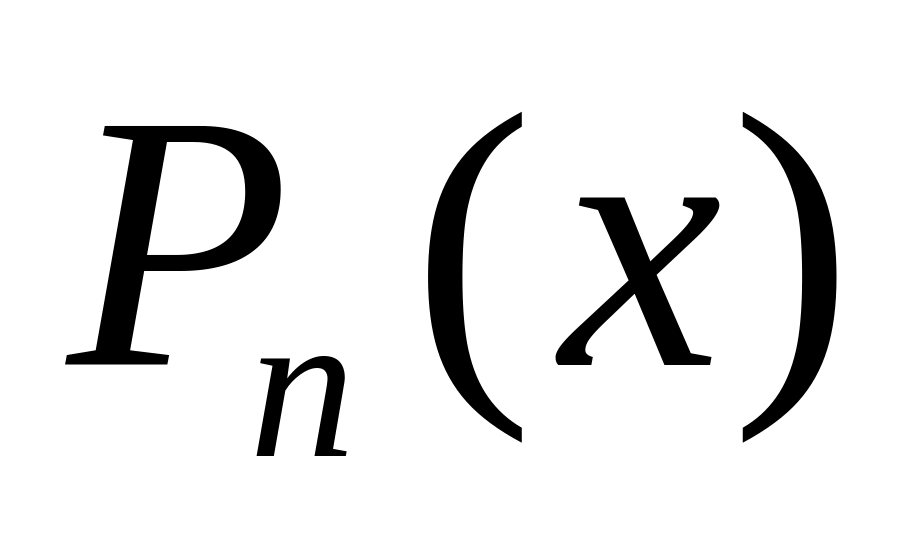
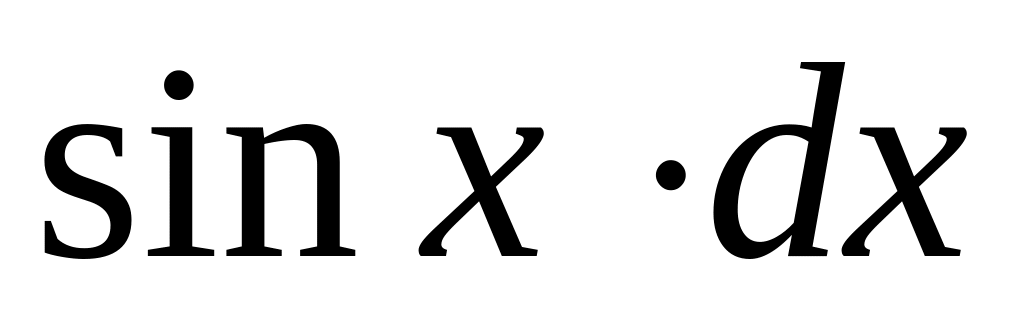
2
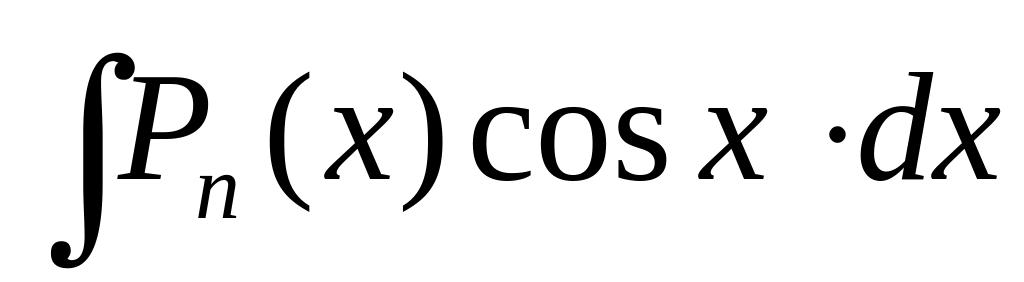
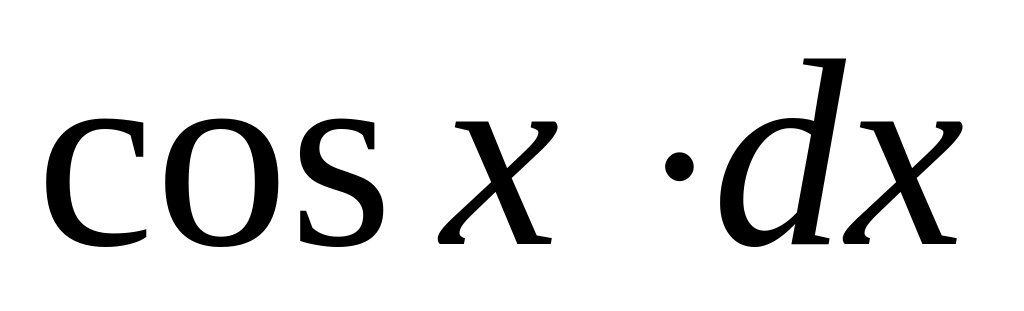
3
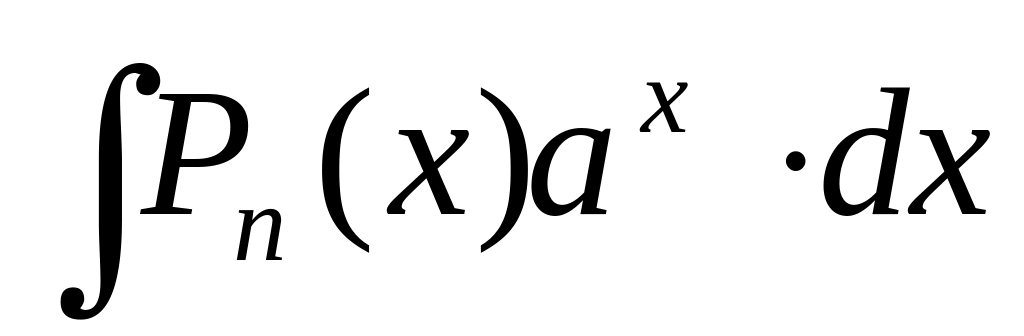
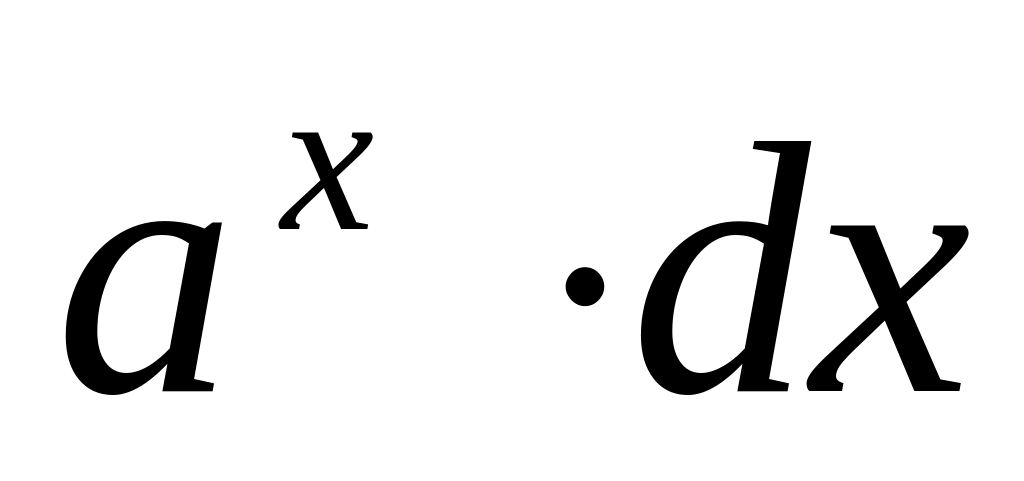
4
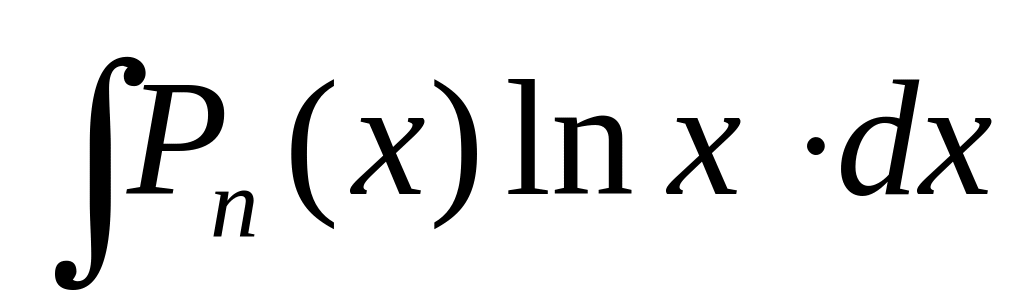
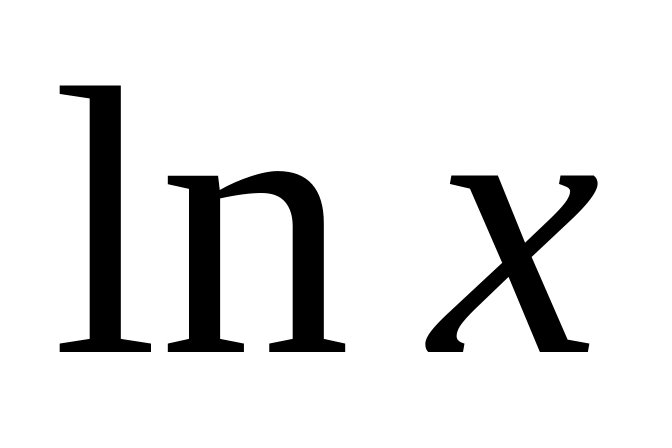
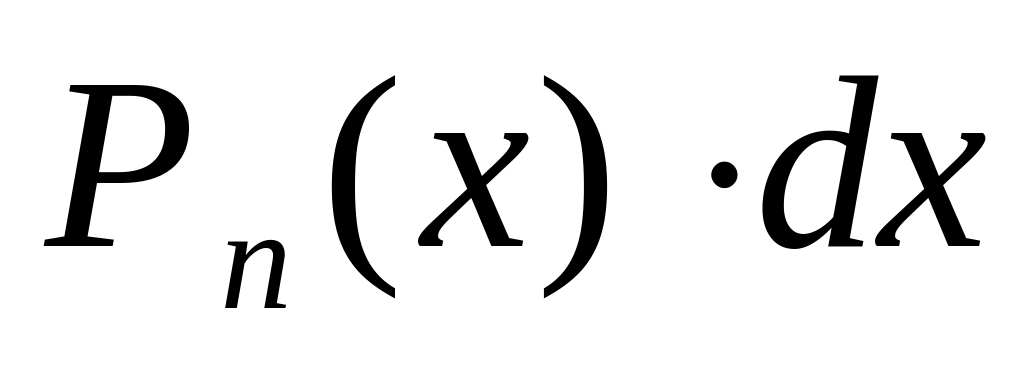
5
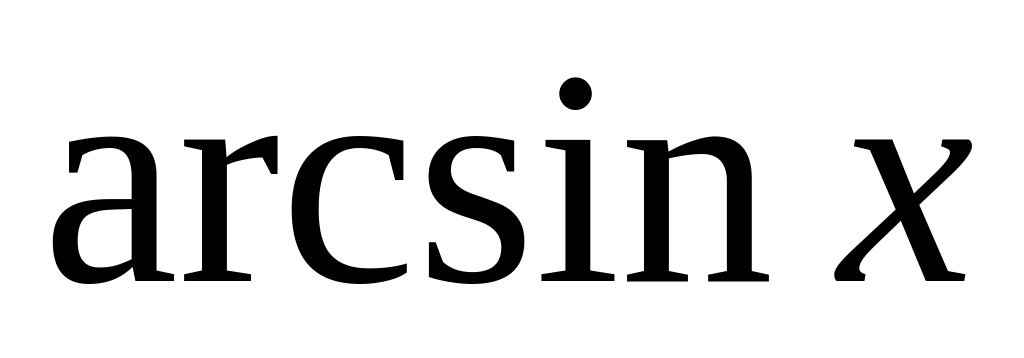
6
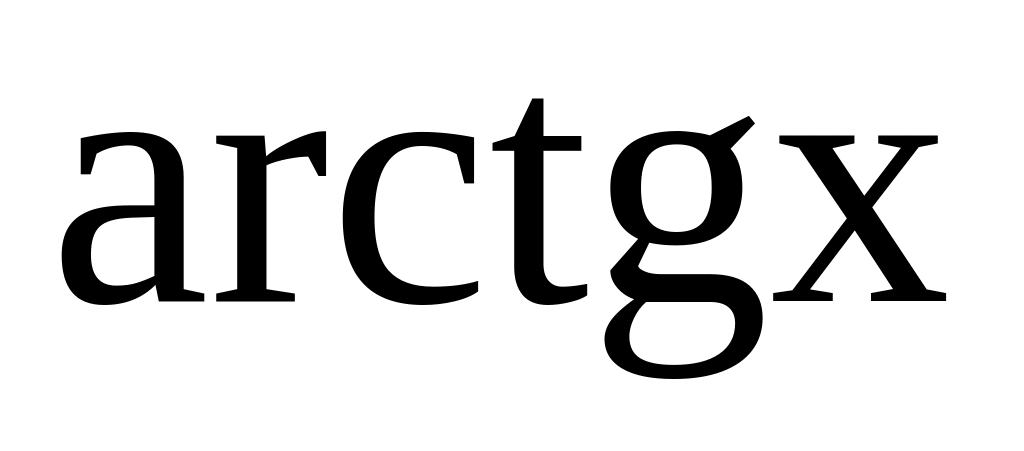
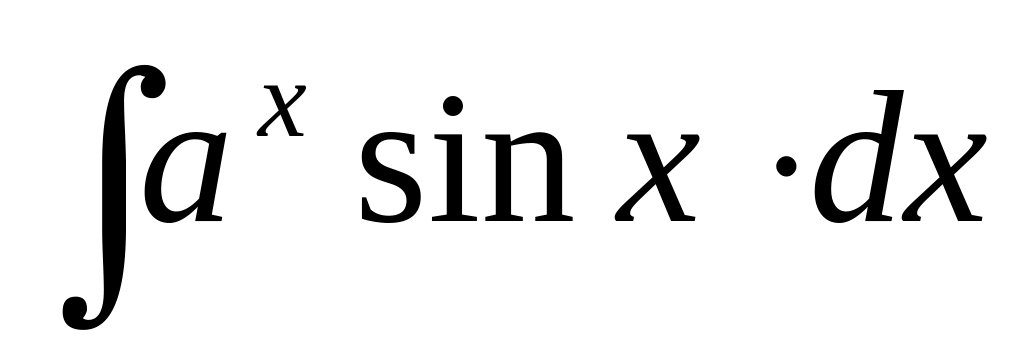
7	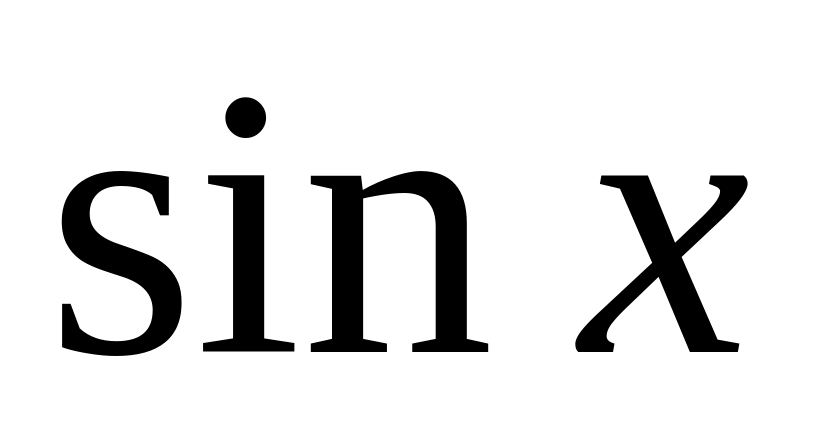или	или
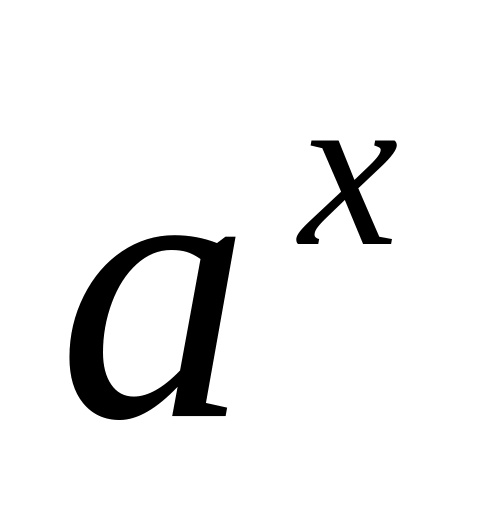
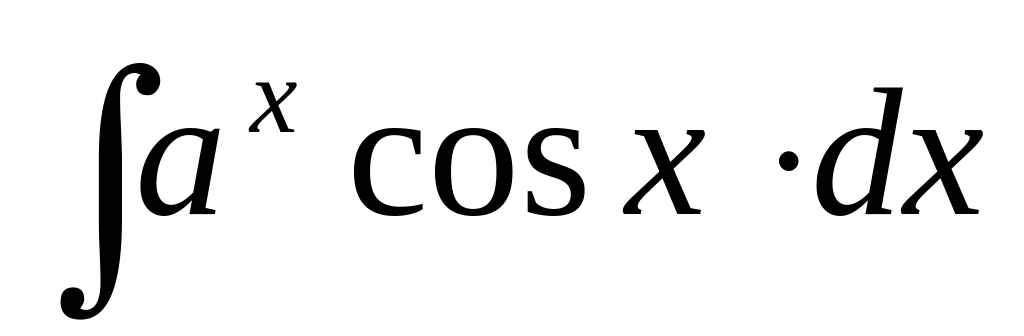
8	или	или
9
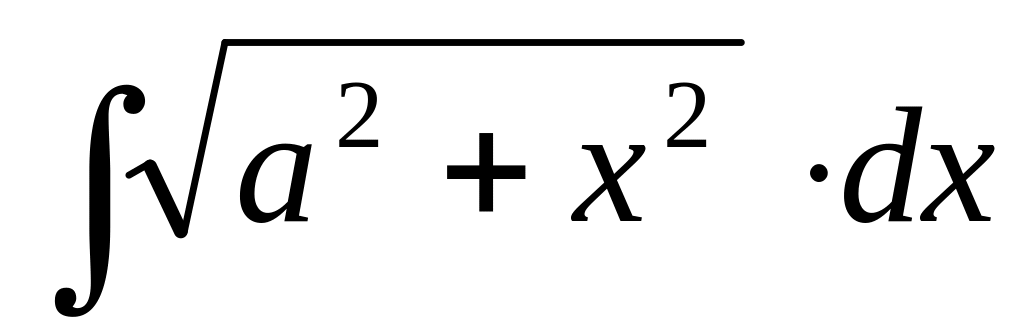
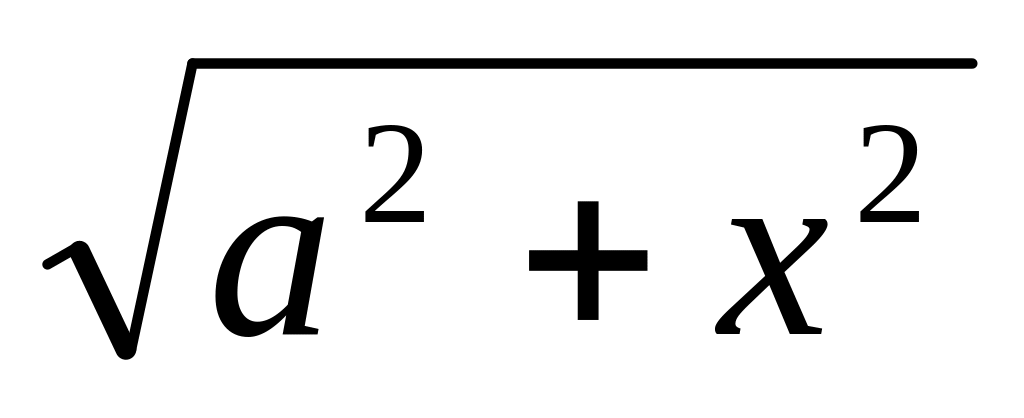
10

Замечания

1 Иногда формулу (2) приходится использовать несколько раз. В интегралах 1-3 это зависит от степени многочлена , а в интегралах 4-6 от степени трансцендентной функции.

2 Интегралы 7-10 являются циклическими интегралами

Применяя формулу интегрирования по частям найдите интегралы.