2.4 Интегралы вида: ,
Интегралы данного вида находятся путем выделения полного квадрата из данного
квадратного трехчлена по формуле:
(**)
и применения правил 1,2.
Интеграл , после выделения полного квадрата сводится к формулам 9 или 10.
Интеграл , после выделения полного квадрата сводится к формулам 8 или
11.
50
|выделите
в знаменатели ПФ полный квадрат по
формуле (**)| =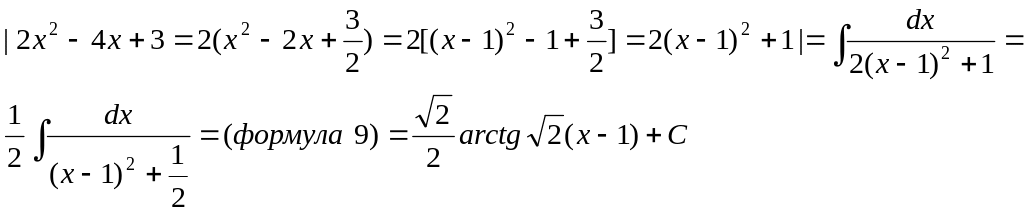 
51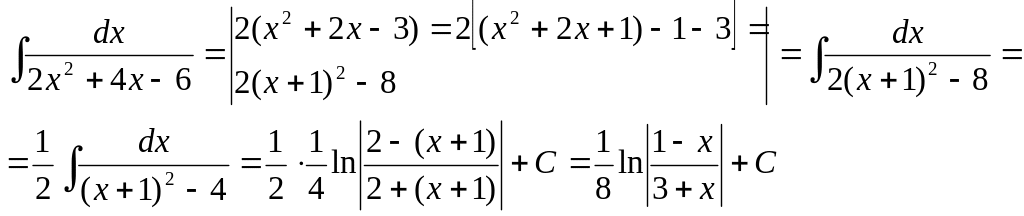 
52
=
(сомножитель (-1) внесем в квадратные
скобки, получим
)=
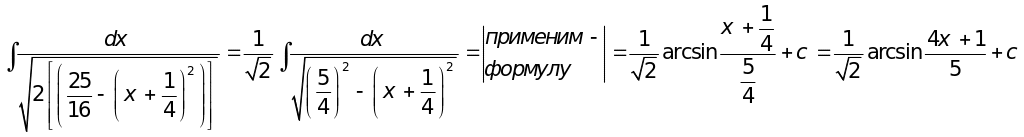
Выполните самостоятельно
53
54
55
56
2.2.3 Интегрирование дробных функций (рациональных или иррациональных), когда в знаменатели или под корнем в знаменатели стоит функция, производная которой равна числителю (или приводится к числителю).
Интегралы этого вида находятся путем замены многочлена стоящего в знаменателе ПФ новой переменной
57
Замечаем,
что производная знаменателя ПФ
,
отличается от числителя только
постоянным множителем. Выполним
интегрирование, за новую переменную
примем
58
Легко заметить, что если в числителе стоит производная знаменателя, то интеграл всегда равен натуральному логарифму знаменателя.
59
60
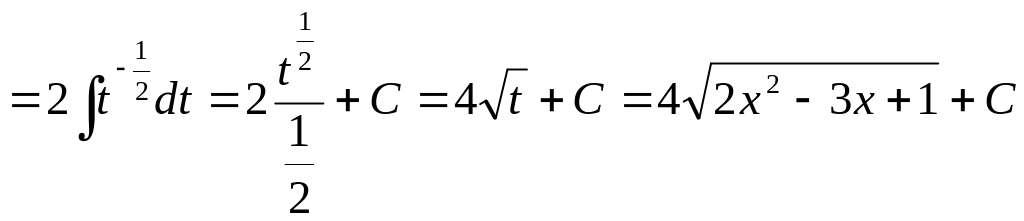
61
Правило 3
-
Если под знаком интеграла стоит дробная функция (рациональная или иррациональная), в знаменателе которой или под корнем в знаменателе содержится функция, производная которой равна числителю (или приводится к числителю), то интеграл вычисляется способом замены переменной, причем функция, стоящая в знаменатели обозначается за t.
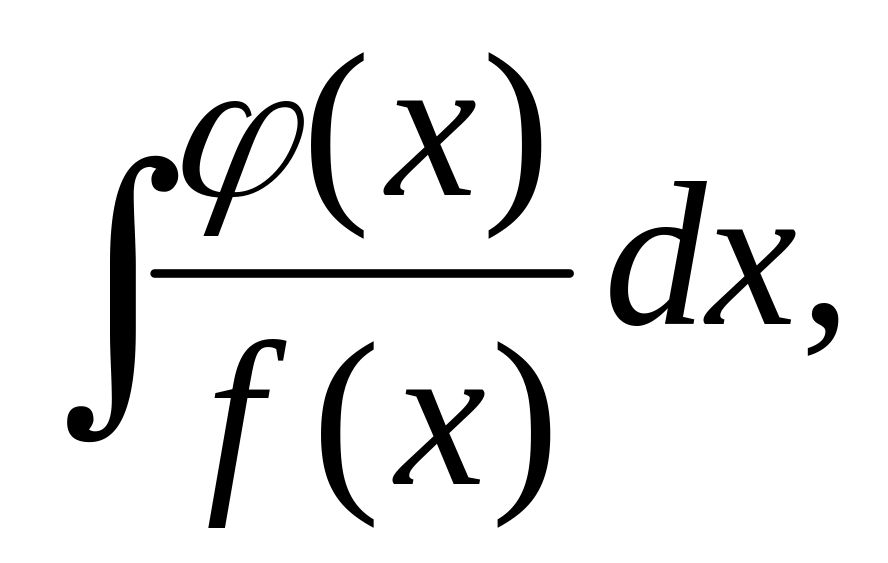где
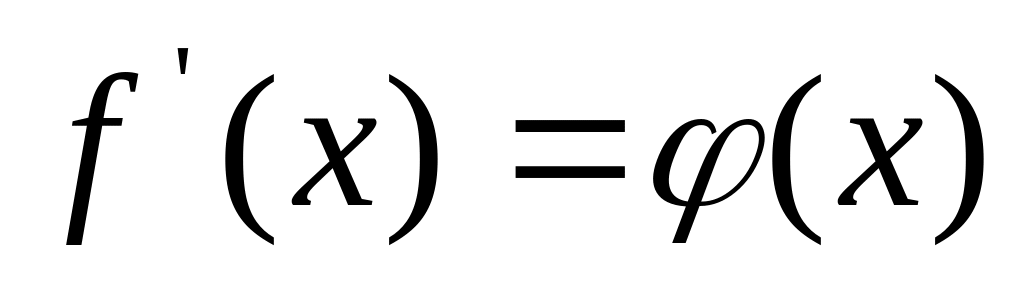или
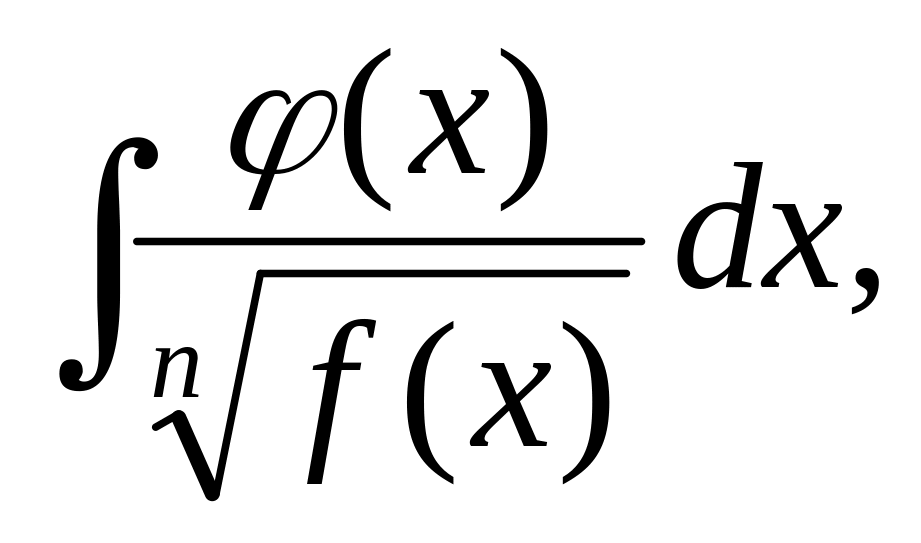где
,
то
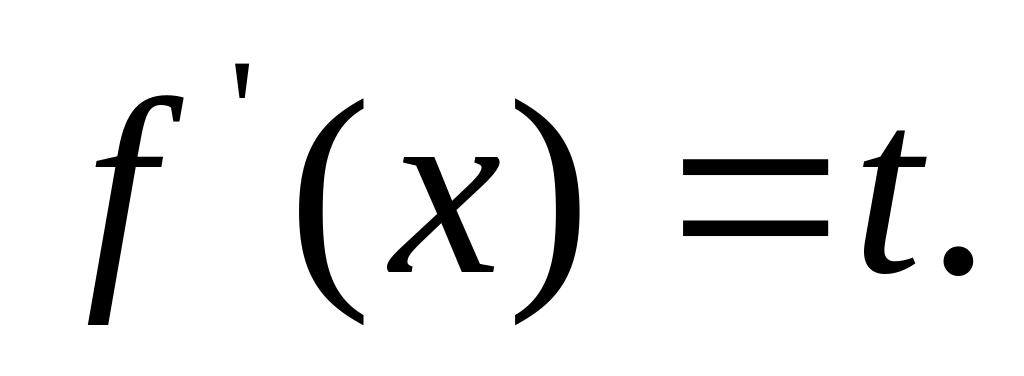
Выполните самостоятельно
62
63
64
65
2.2.4 Интегралы вида:
В пункте 2.2.4 рассмотрим интегралы, в которых ПФ представлена как произведение сложной функции и производной ее промежуточного аргумента. В этом случае промежуточный аргумент принимается за новую переменную t .
Например
Функция
сложная,
ее промежуточный аргумент равен
,
производная которого
содержится
в ПФ, поэтому интеграл сводится к
табличной подстановке 
Рассмотрим интегралы данного вида
66
67
=
68
69
70
71
72
73
Выполните самостоятельно
74
75
76
77
Правило 4
-
Если под знаком интеграла стоит сложная функция в произведение с производной своего промежуточного аргумента , то интеграл вычисляется способом замены переменной, причем промежуточный аргумент обозначается за t.
,
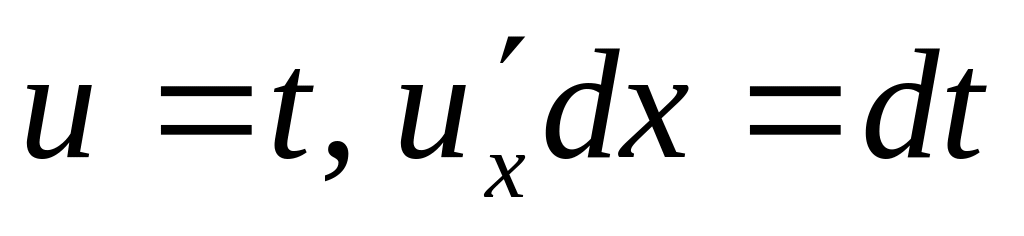
Замечание Используя правило 4 вычисляются интегралы, которые с помощью подстановки сводятся к табличным интегралам по формулам 8-11. (Обратите внимание, что данные интегралы имеют «специфический» вид).
78
79
80
81
Выполните самостоятельно
82
83
84
85
