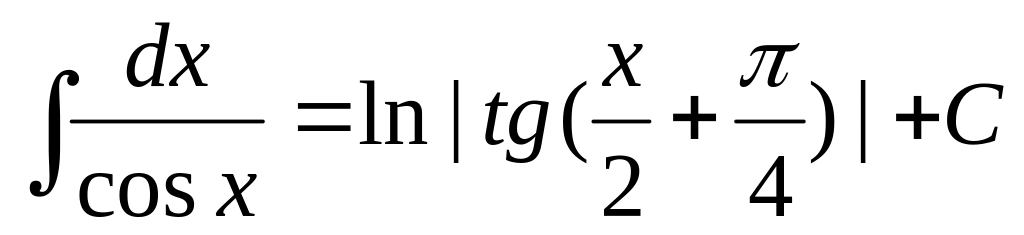Пояснительная записка
Настоящее учебно-методическое пособие состоит из двух частей:
1 Неопределенный интеграл
2 Основные способы интегрирования
2.1 Непосредственный способ интегрирования
2.2 Метод интегрирования подстановкой
2.3 Интегрирование по частям.
Каждый способ структурирован по общим признакам интегрирования, содержит набор интегралов с решениями и для самостоятельного решения студента. Интегралы для самостоятельного решения сопровождаются указаниями и ответами. Такая структура учебно-методического пособия делает его удобным для самостоятельного овладения основными способами интегрирования при минимальной помощи со стороны преподавателя.
В пособии представлены образцы интегрирования функций. По тексту для всех рассматриваемых интегралов предусмотрена единая нумерация.
Непосредственный способ интегрирования
-
1
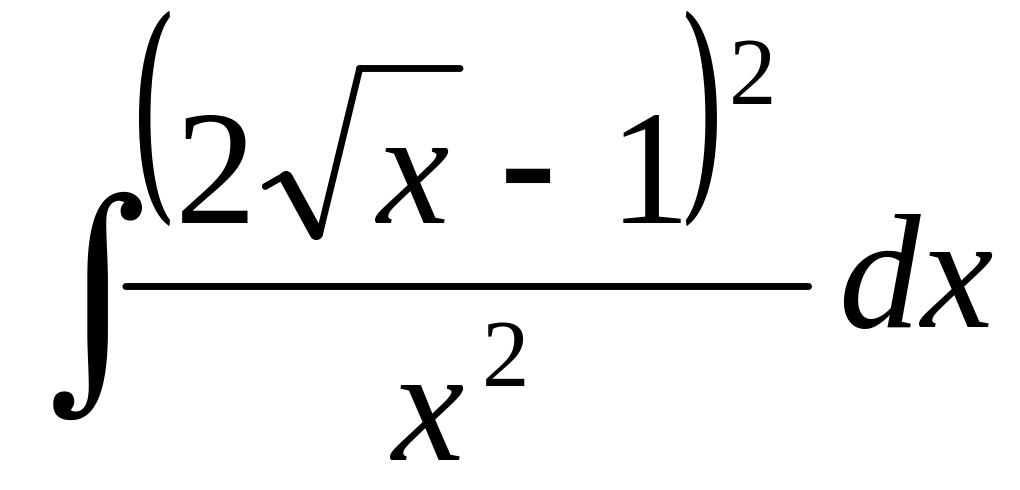
5
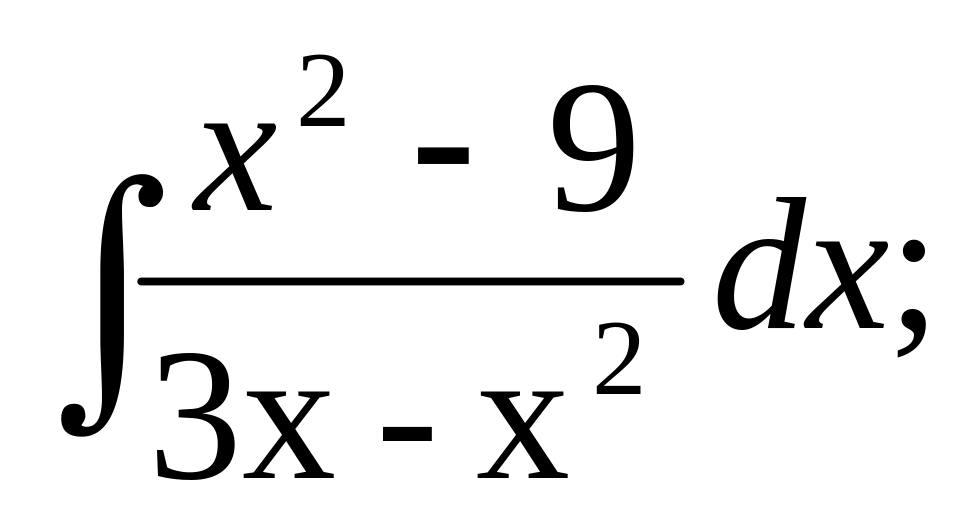
13
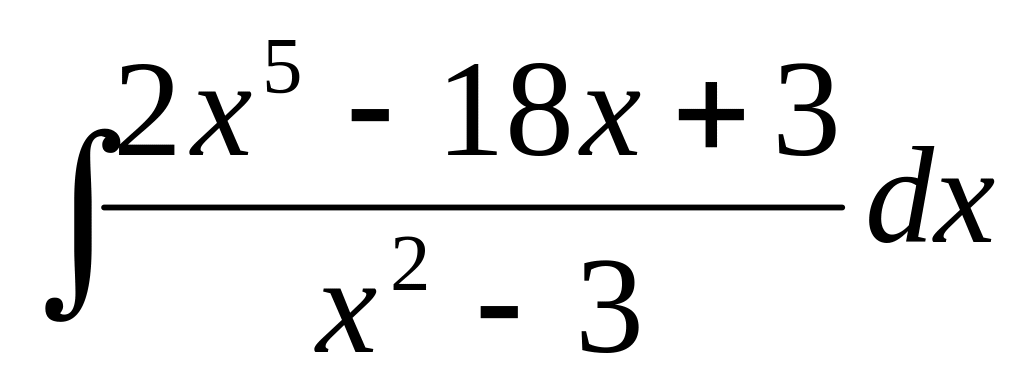
14
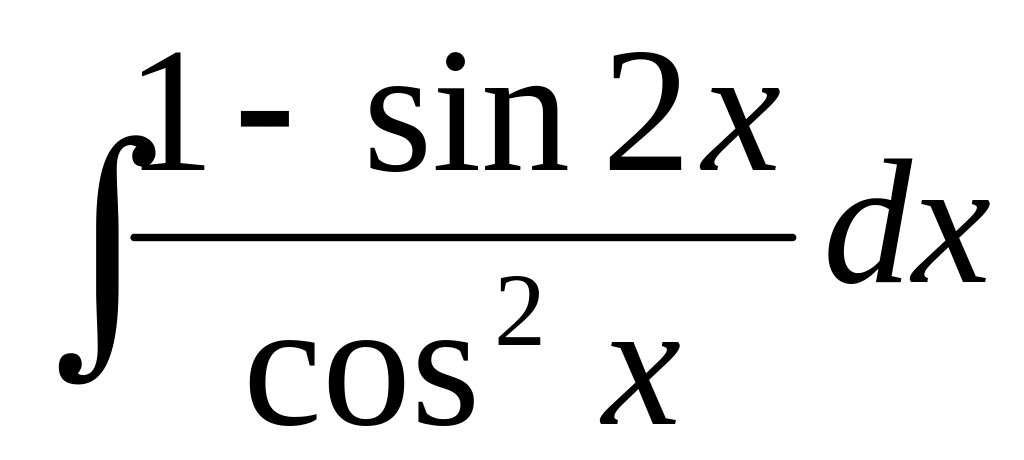
15
16
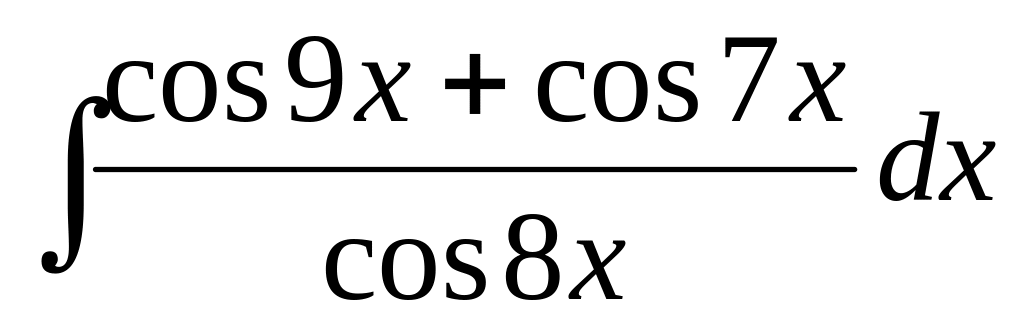
17
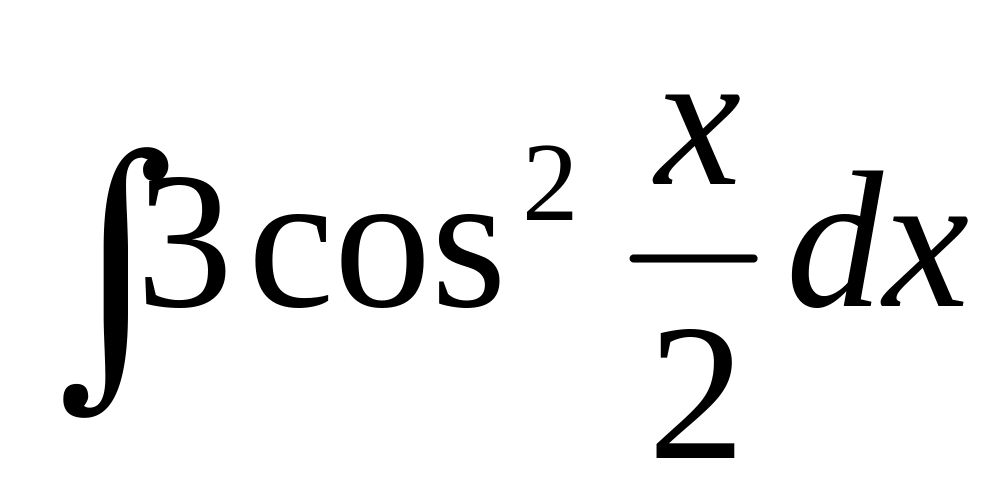
23
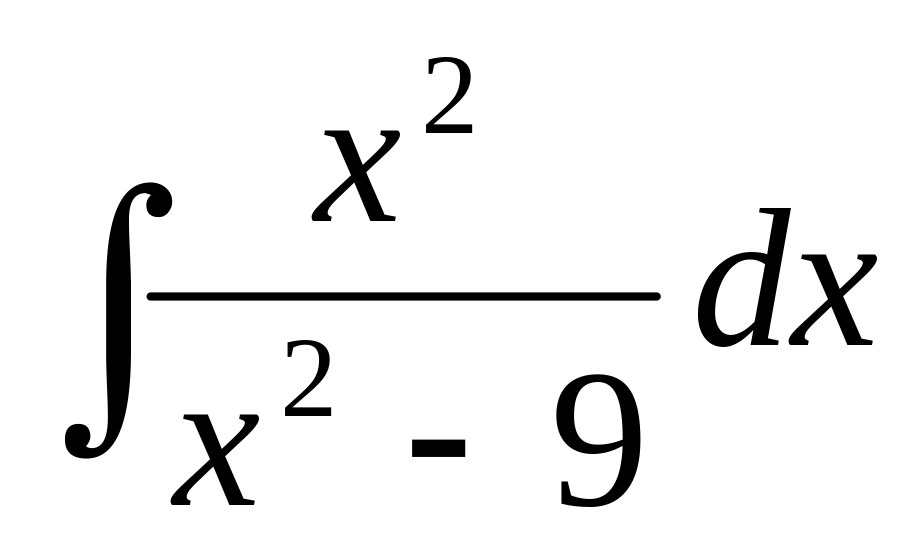
24
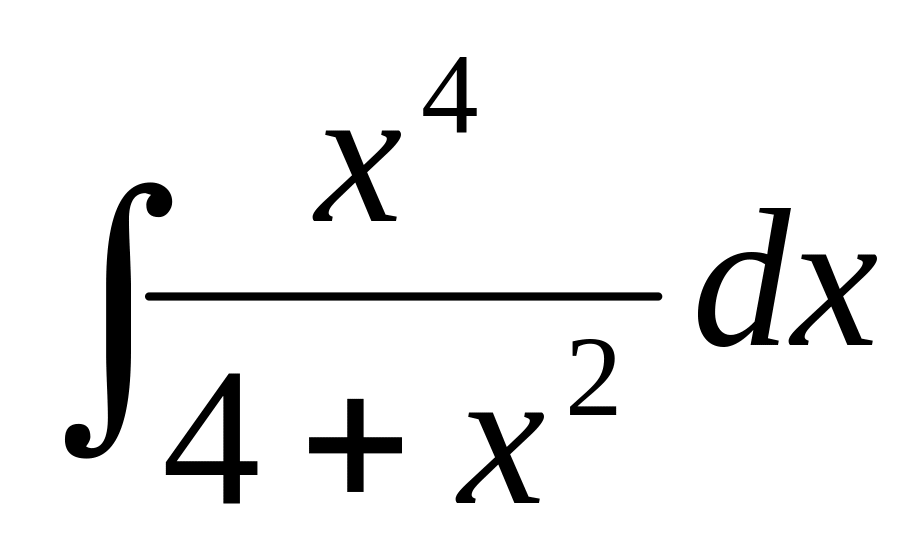
25
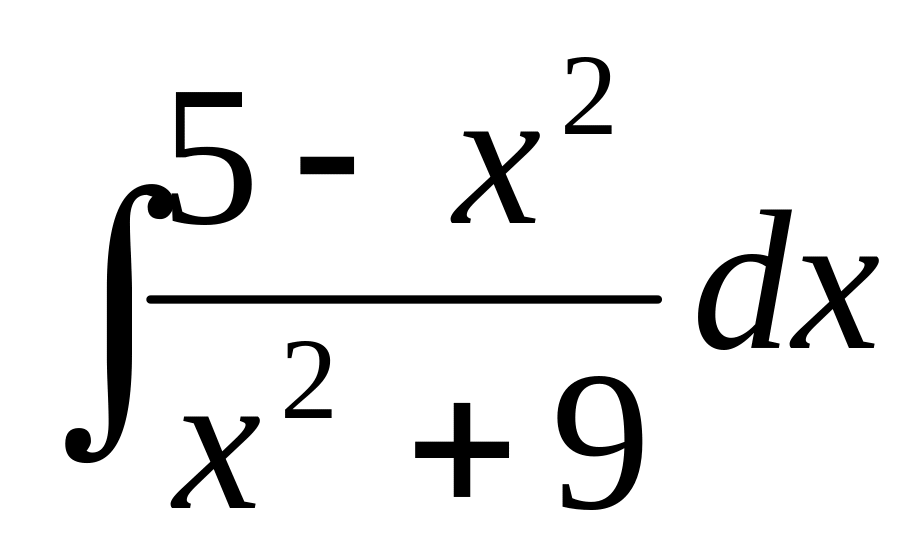
26
Метод интегрирования подстановкой (заменой переменной)
-
32
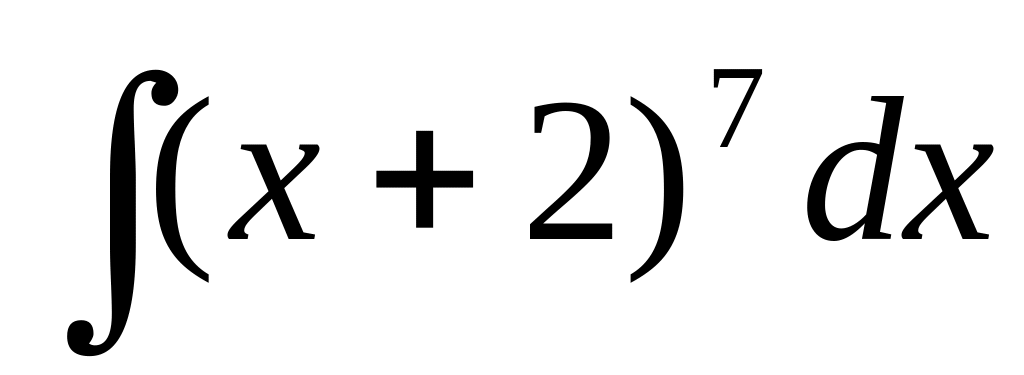
33
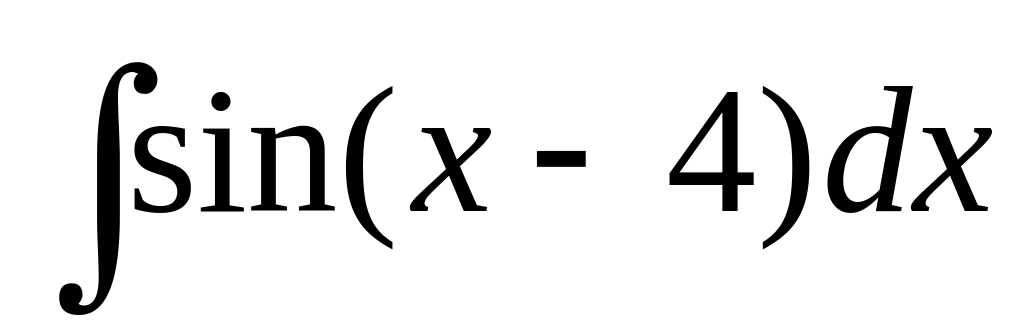
34
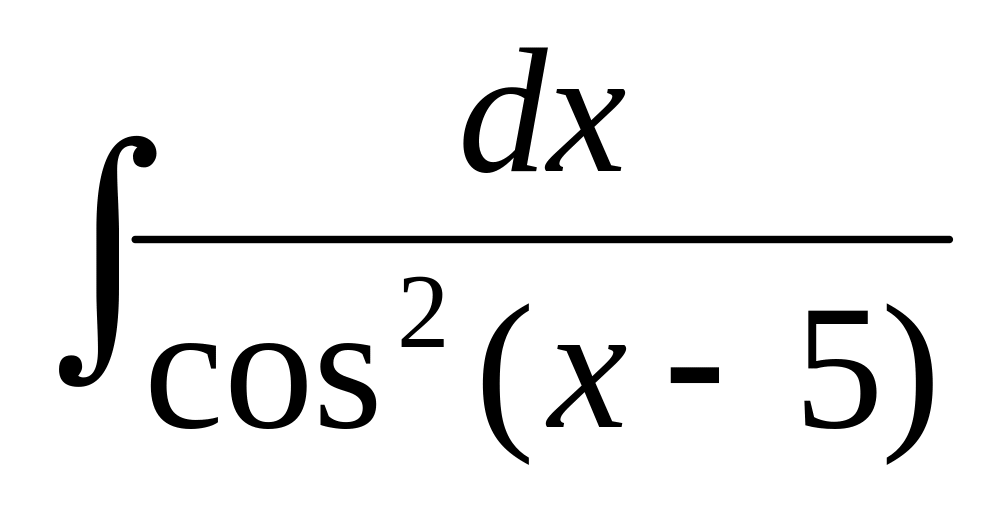
35
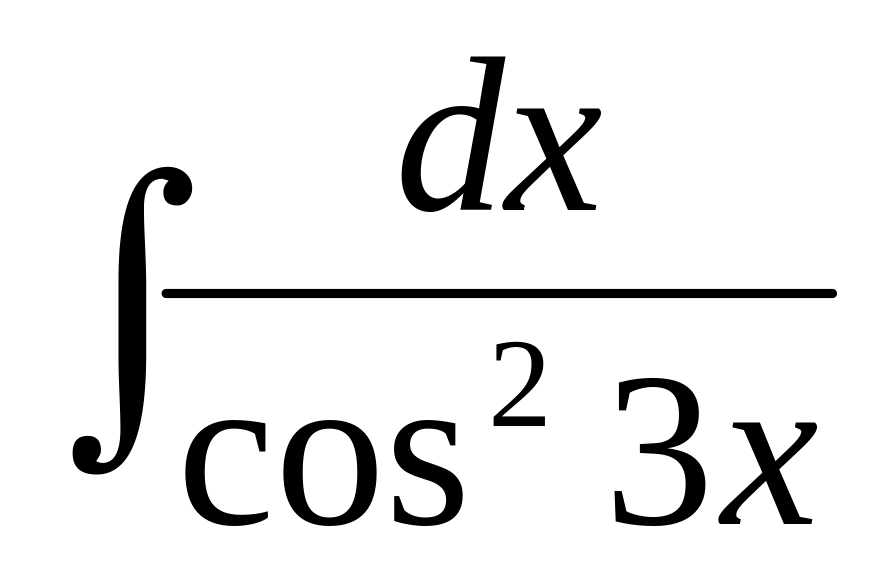
36
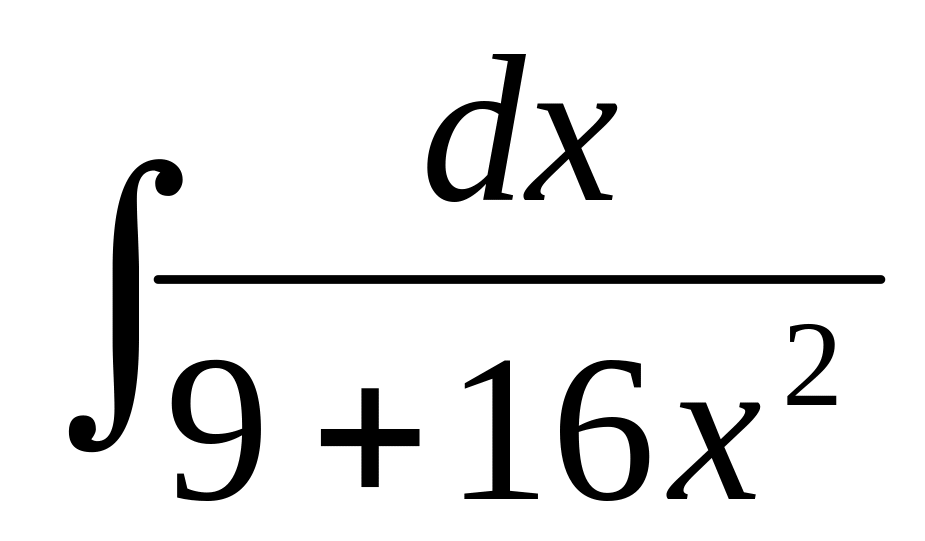
37
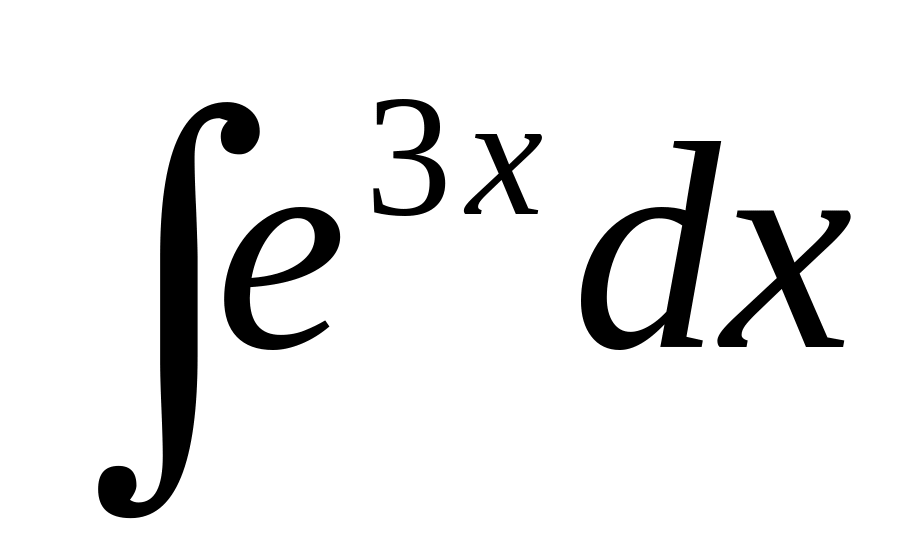
38
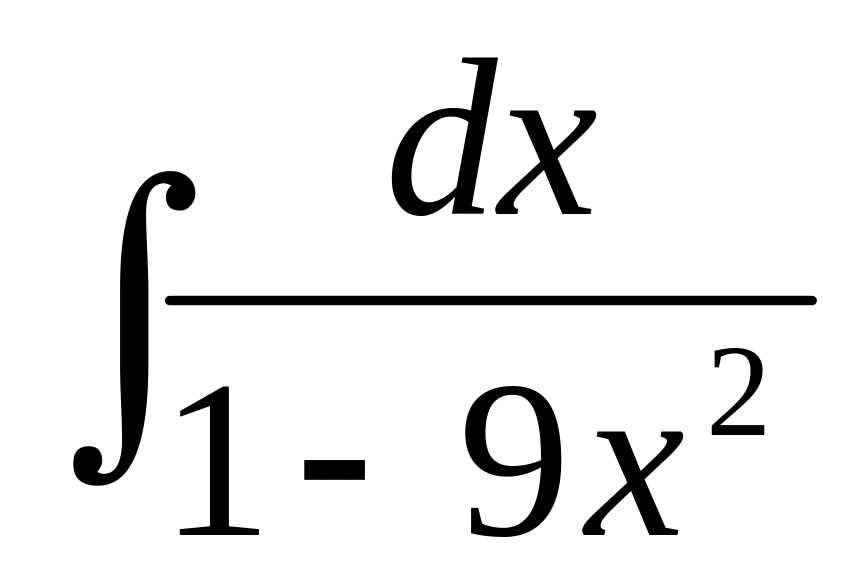
39
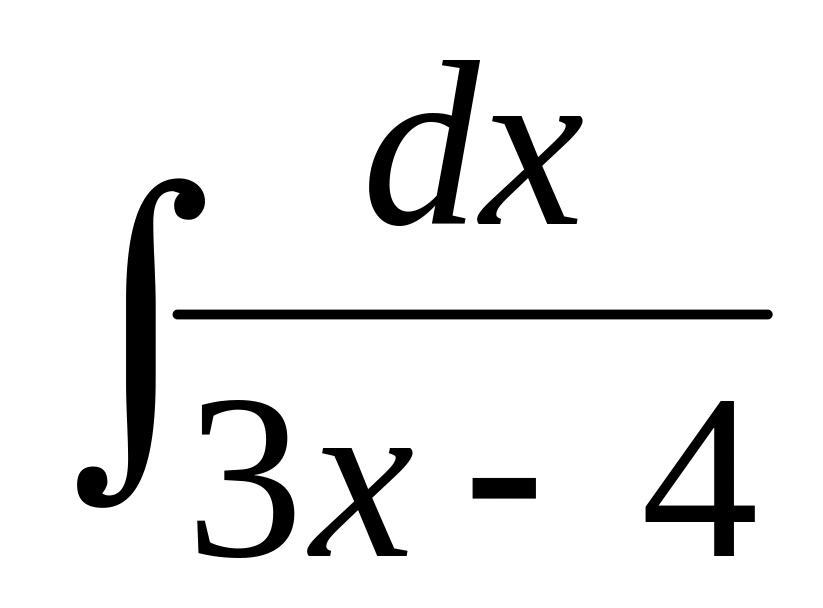
40
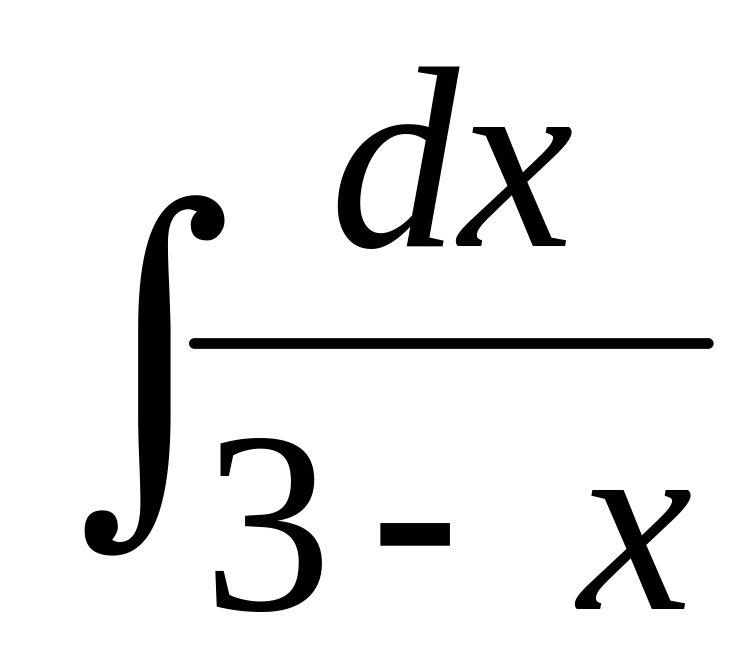
41
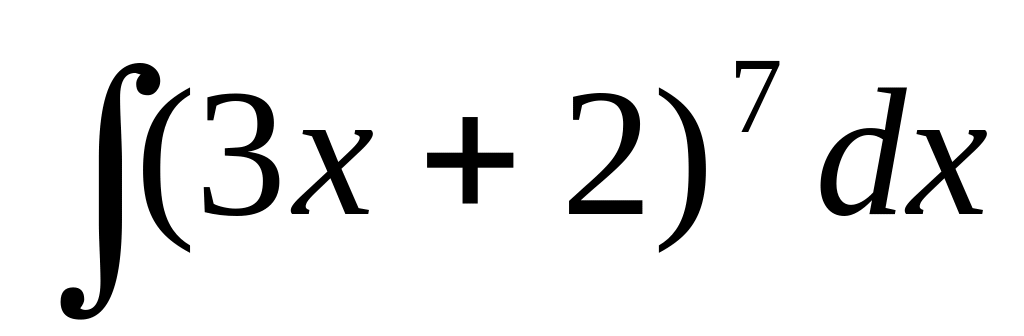
42
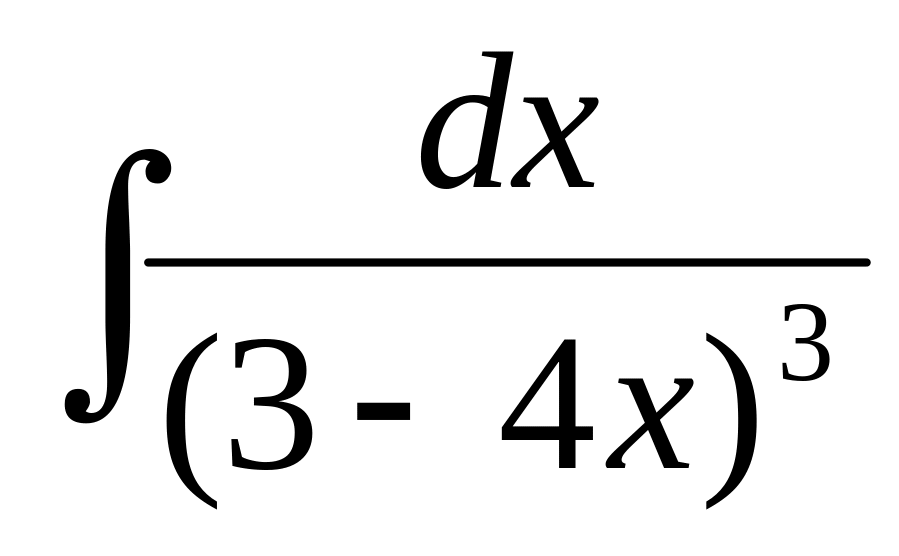
43
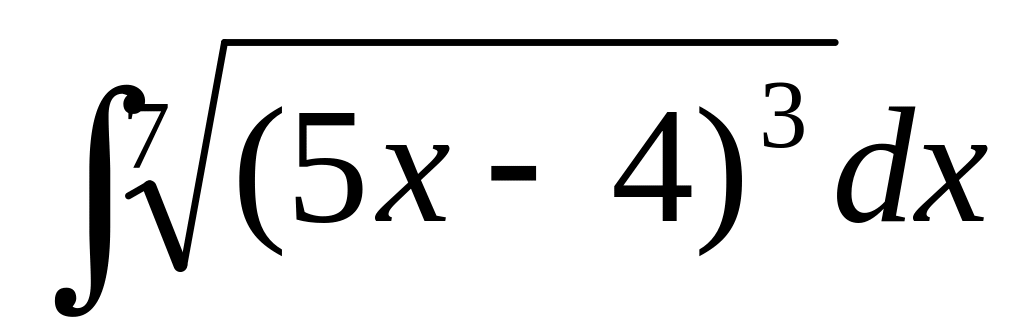
50
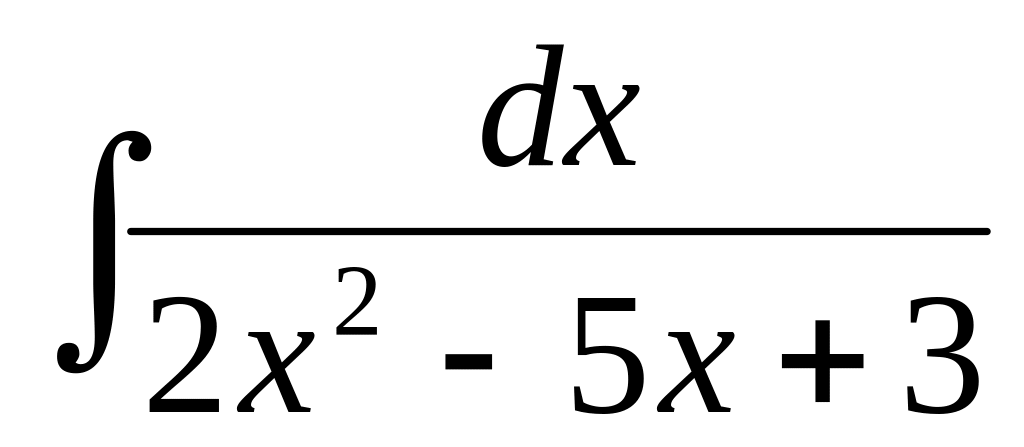
52
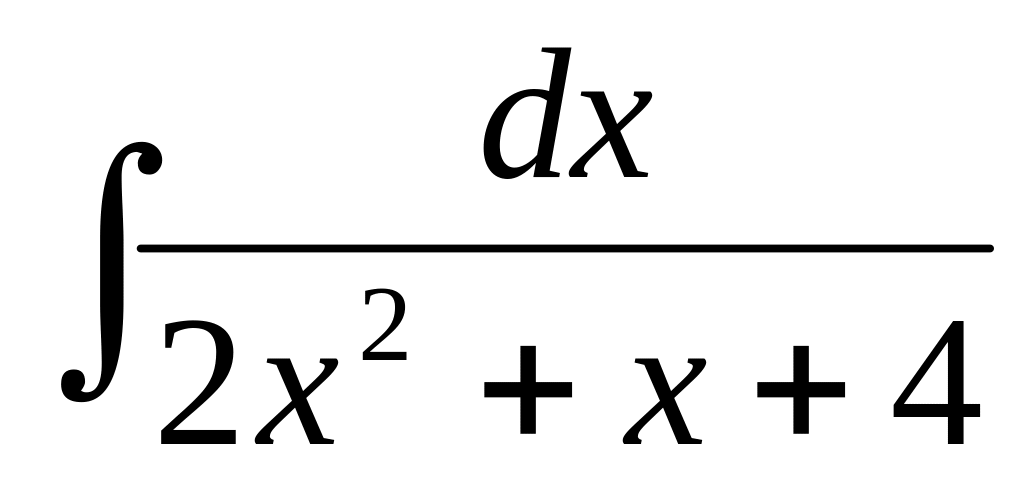
53
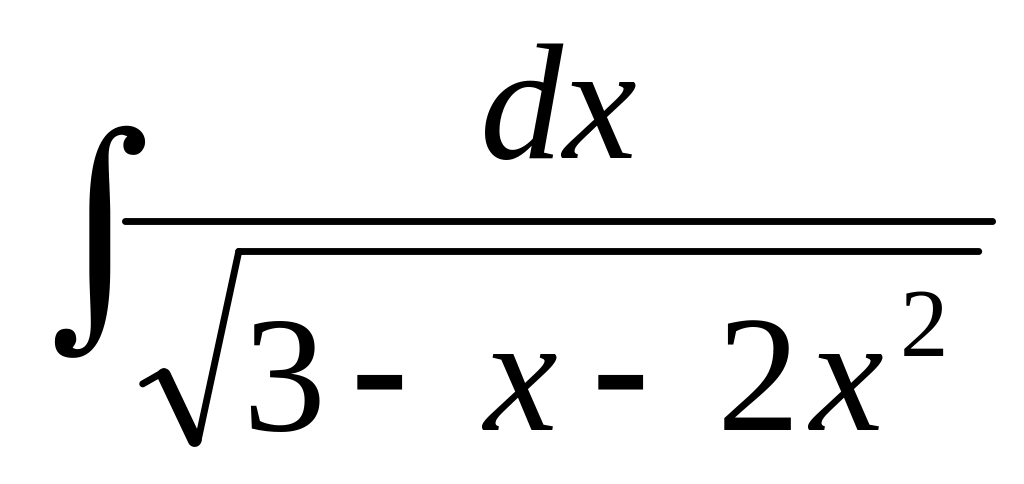
57
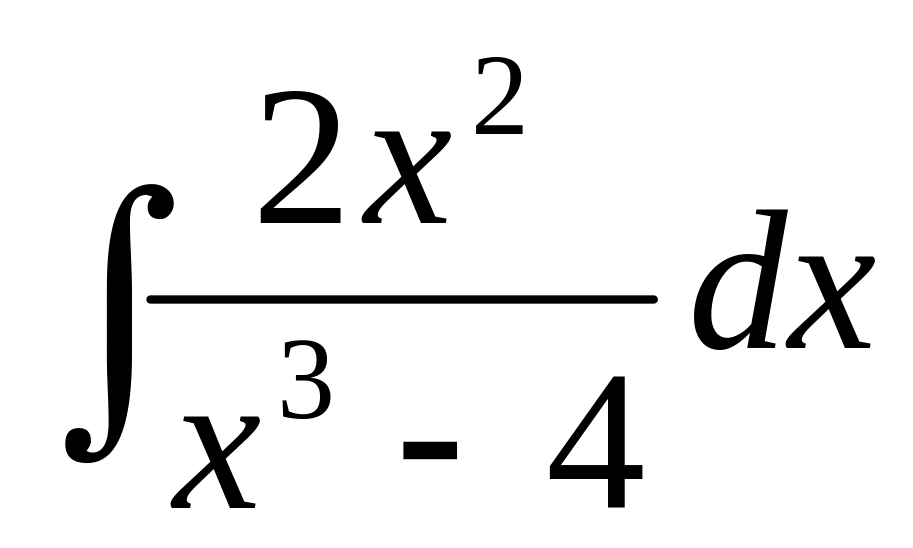
58
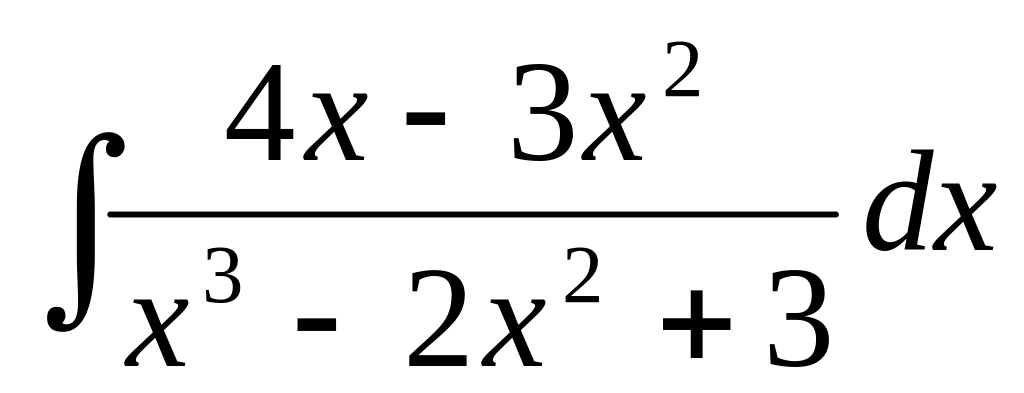
59
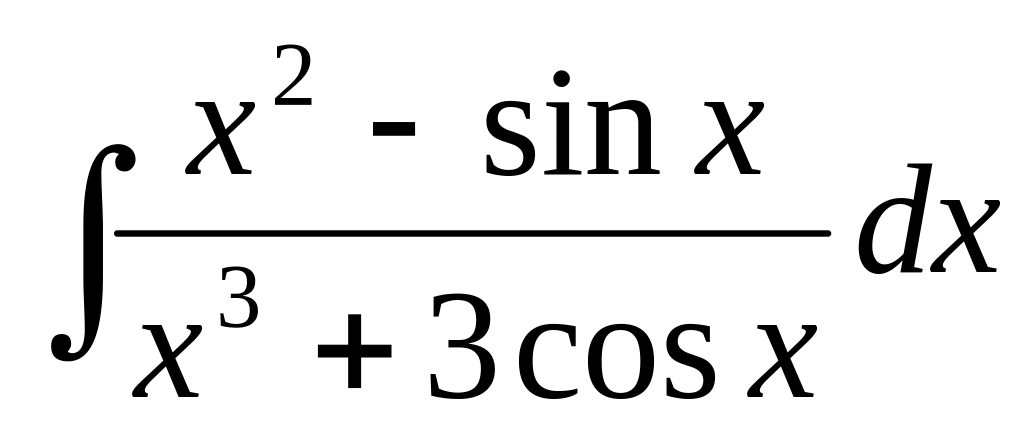
60
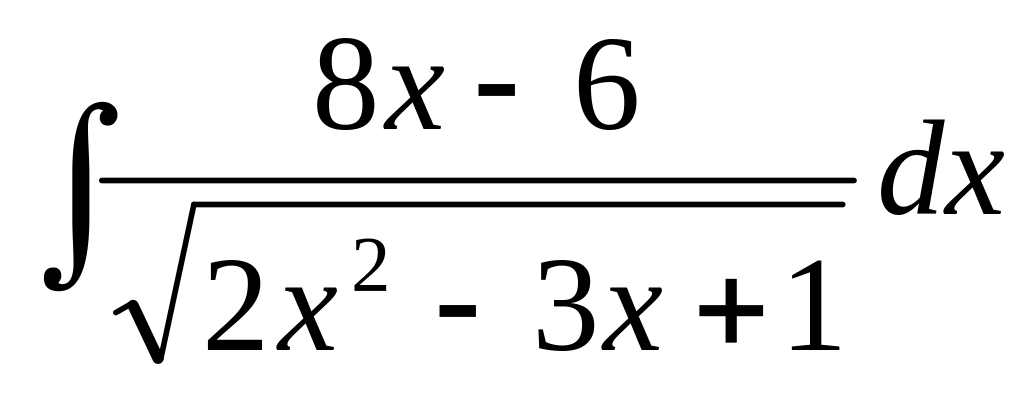
61
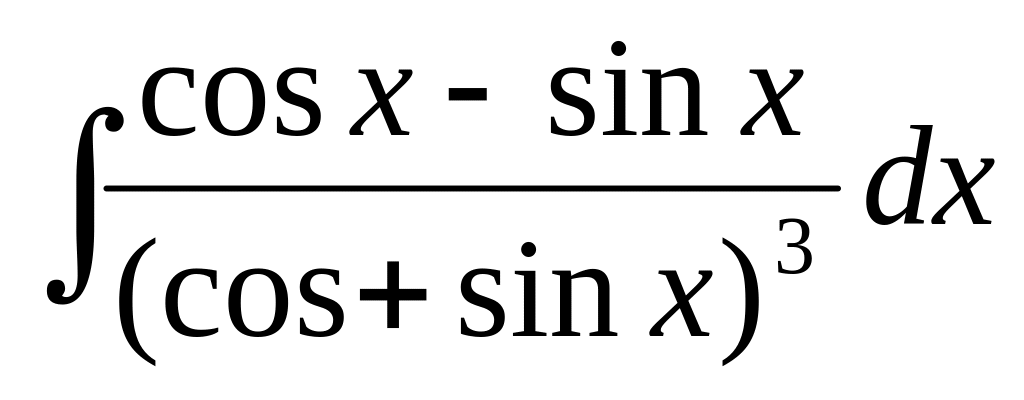
66
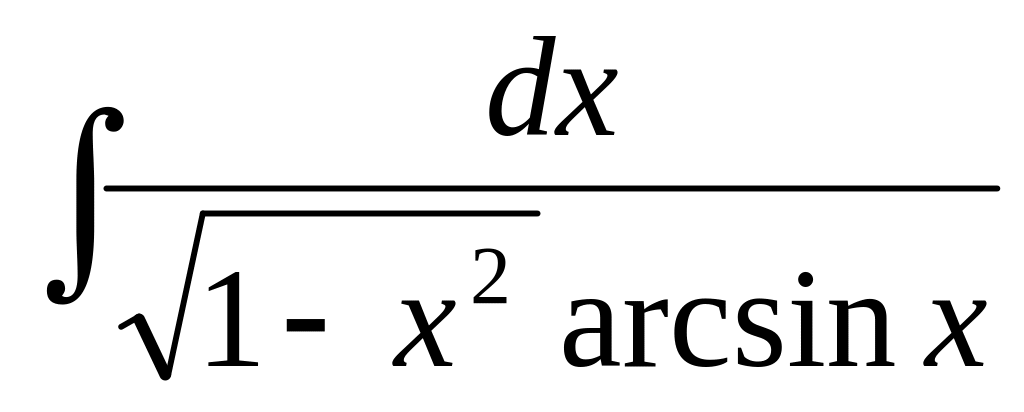
67
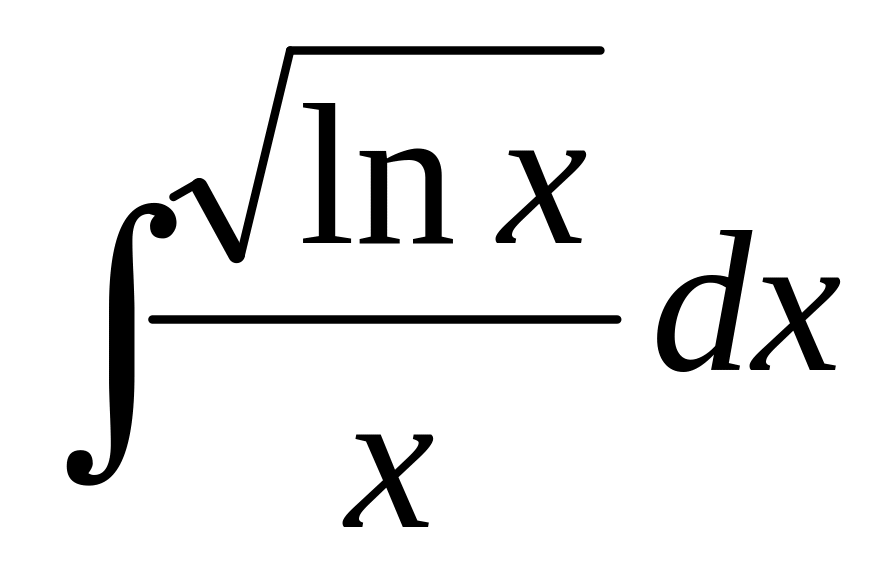
68
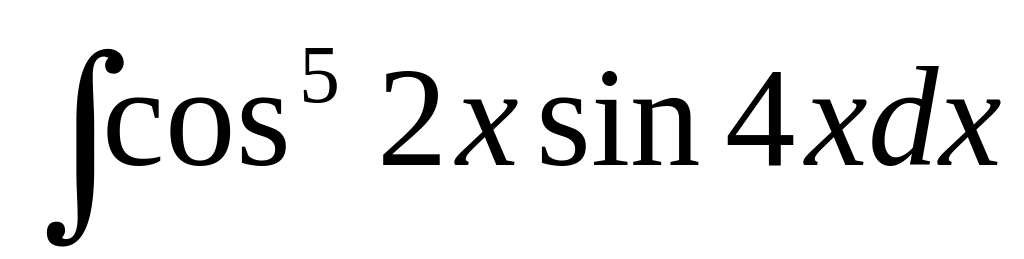
69
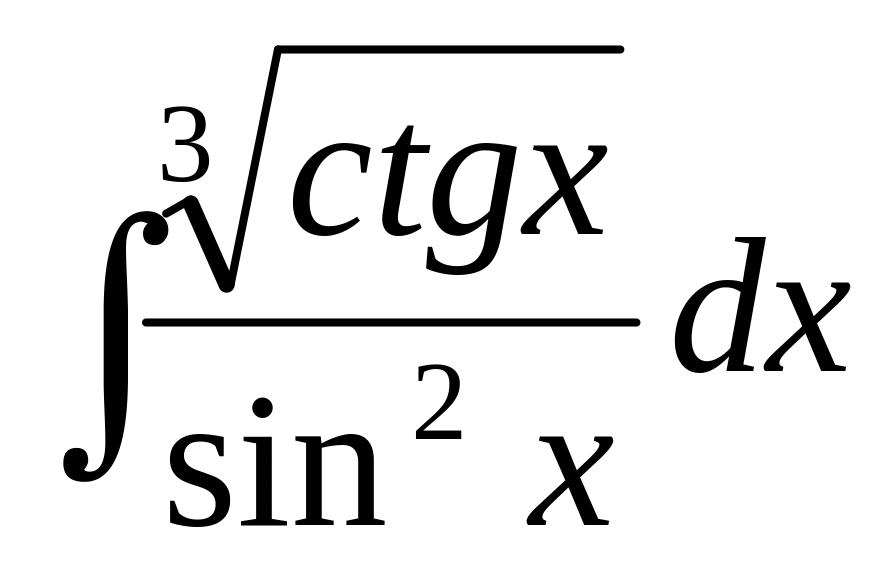
70
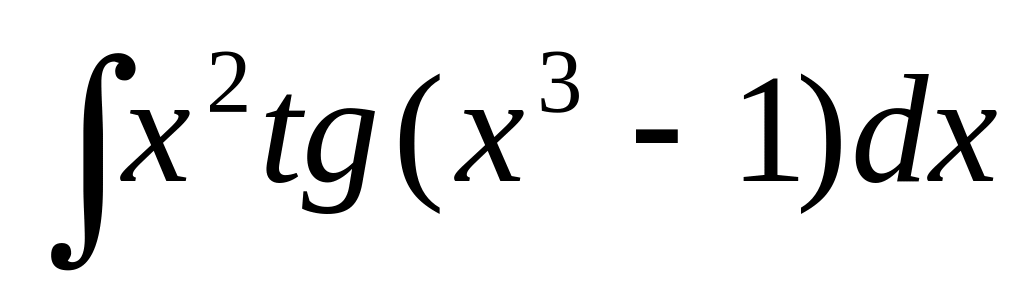
71
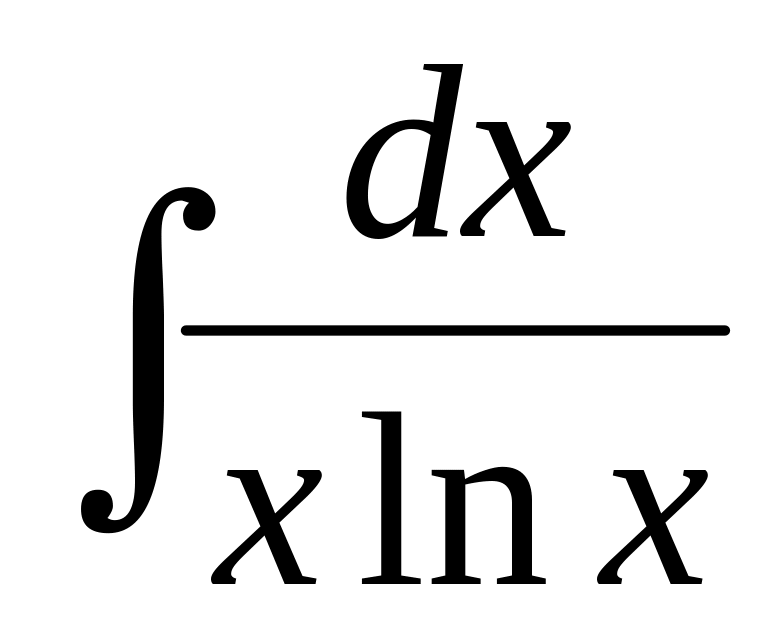
72
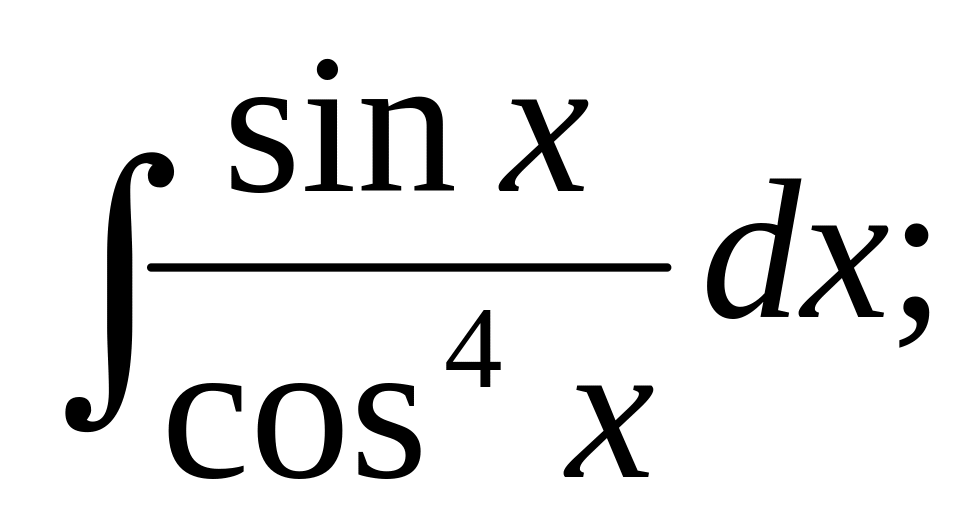
73
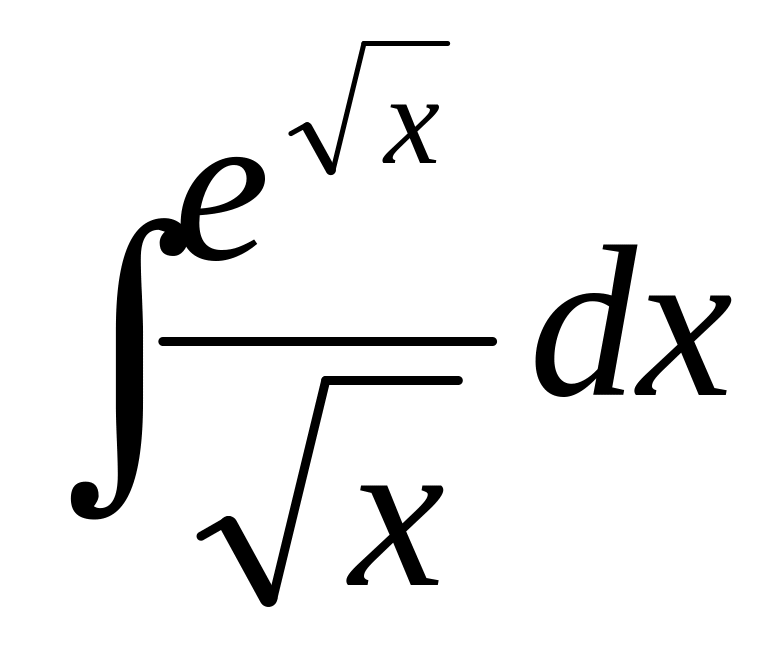
78
79
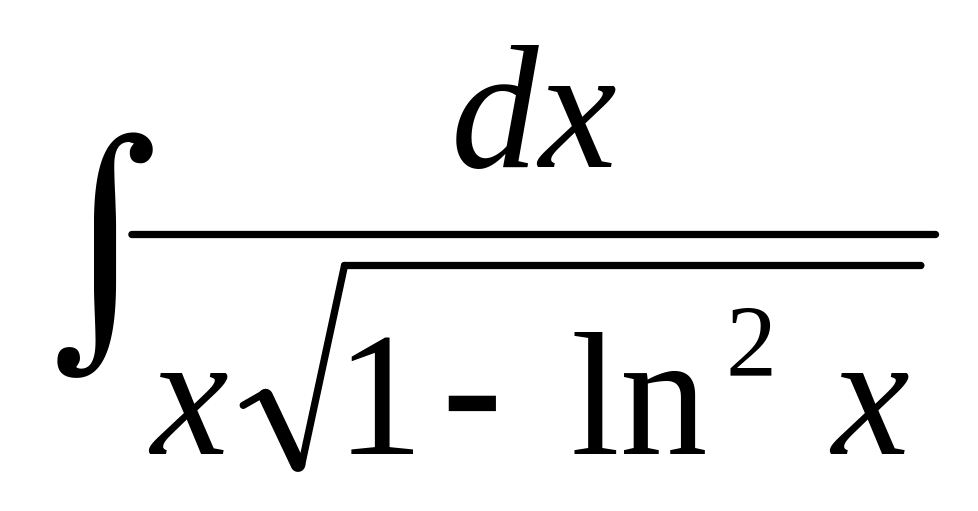
80
81
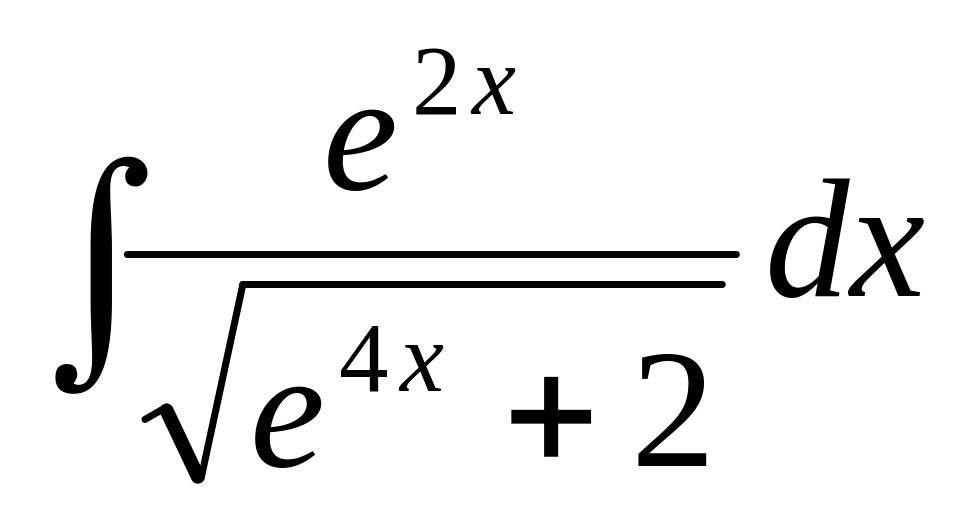
86
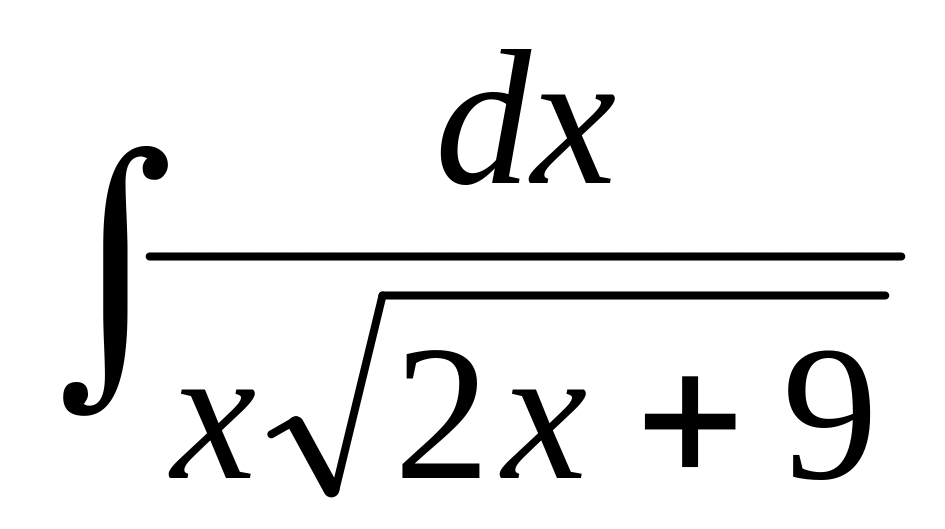
87
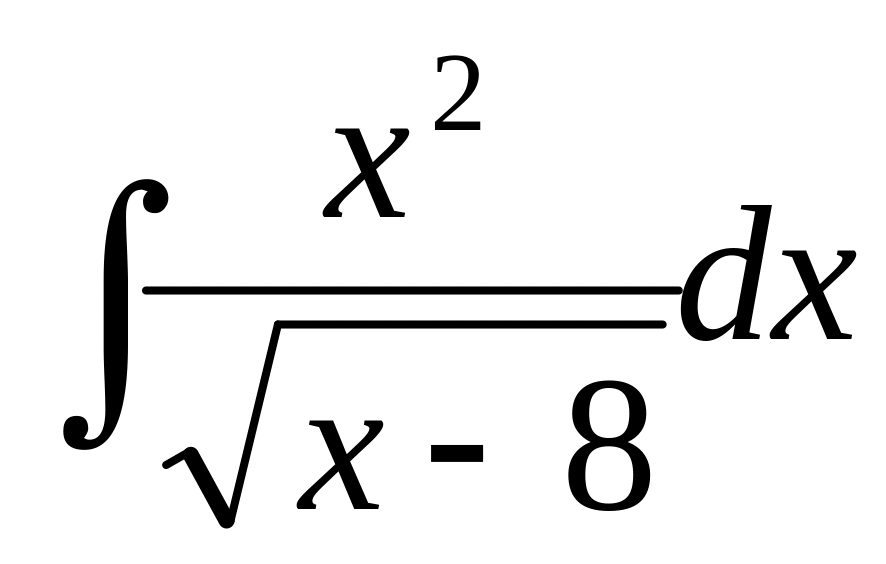
88
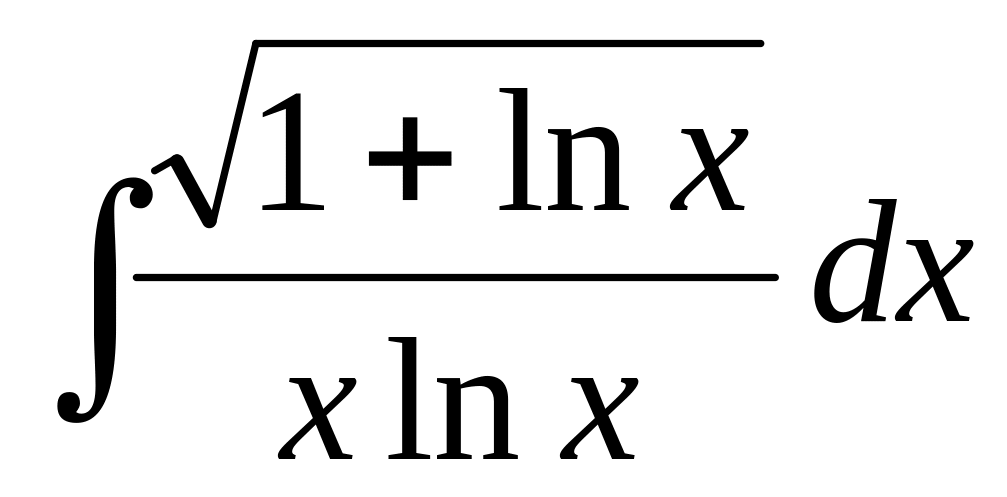
89
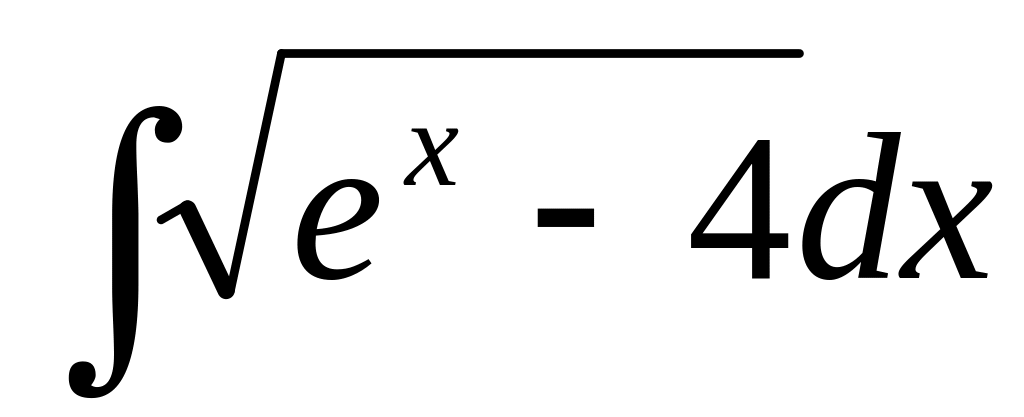
95
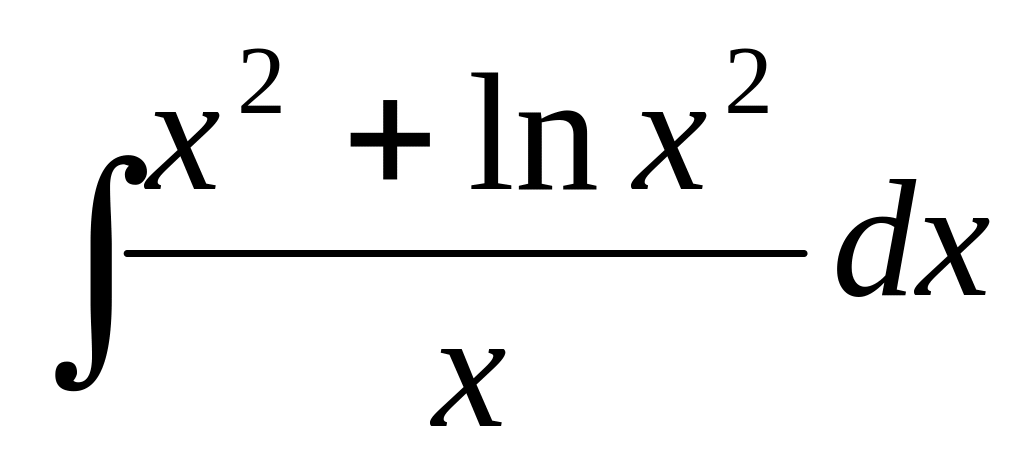
96
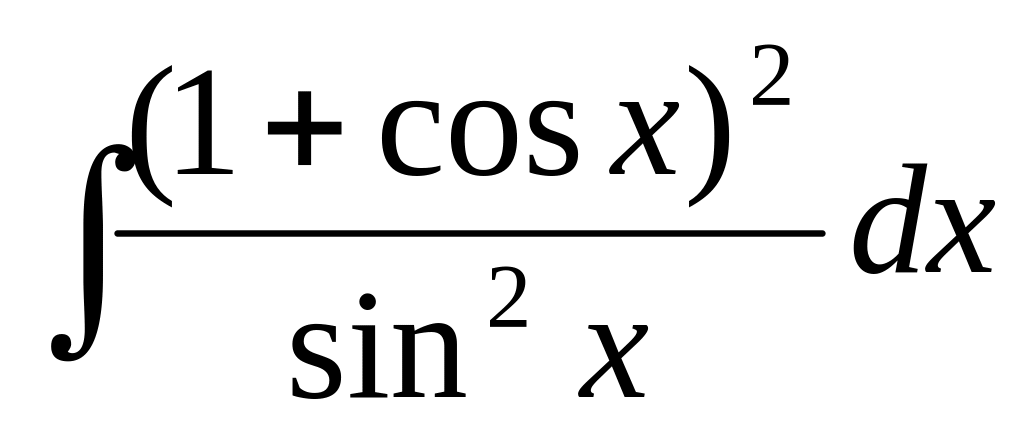
101
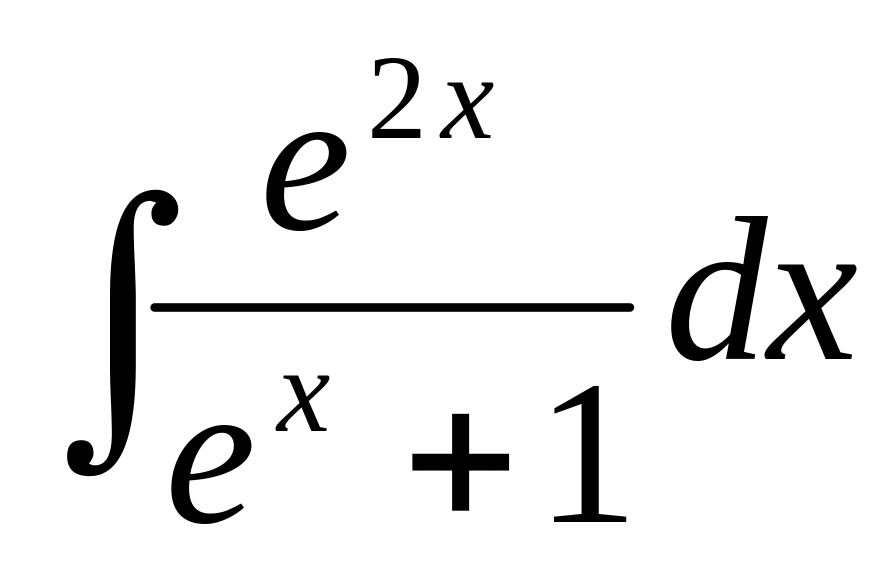
102
Метод интегрирования по частям
-
111
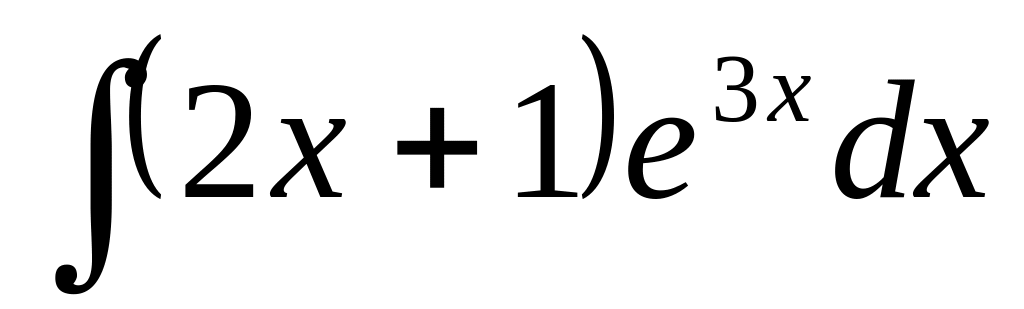
112
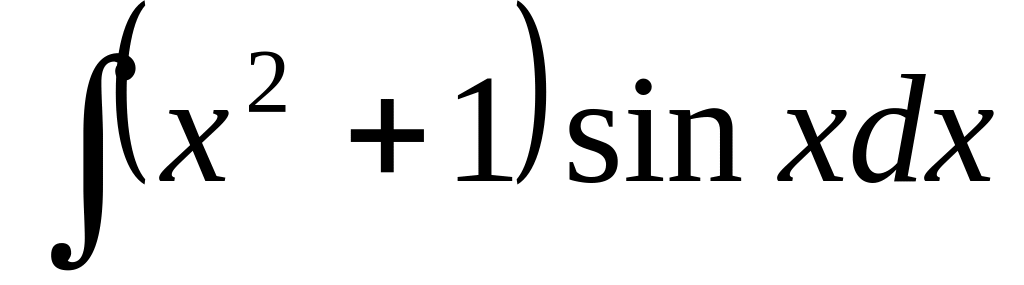
113
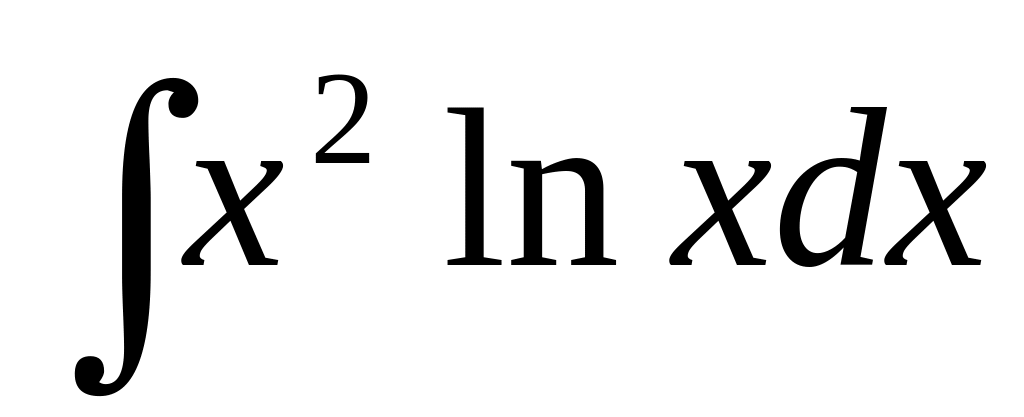
114
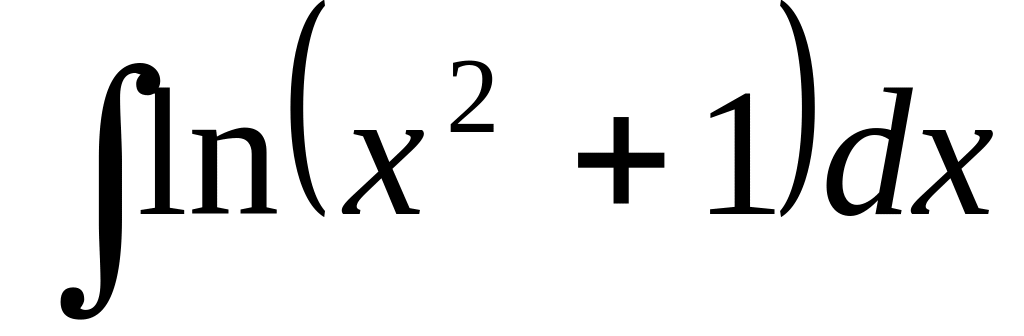
115
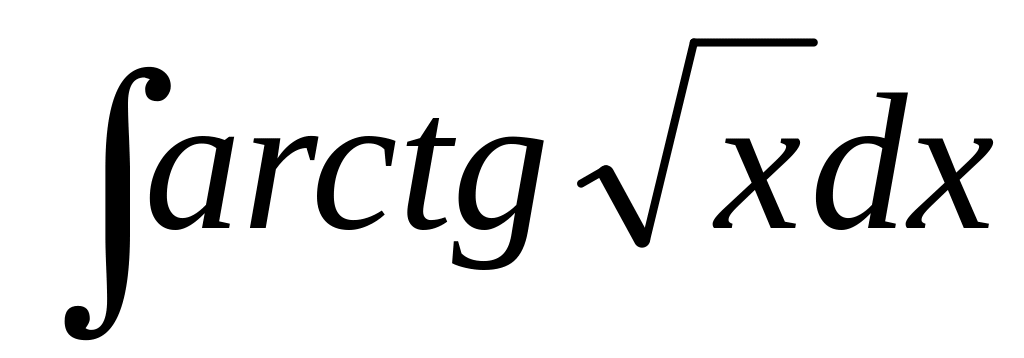
116
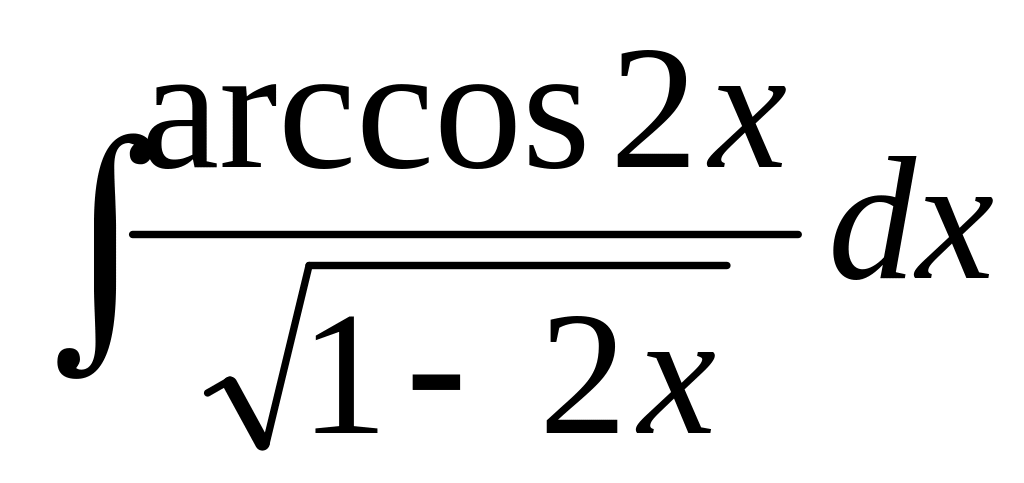
117
118
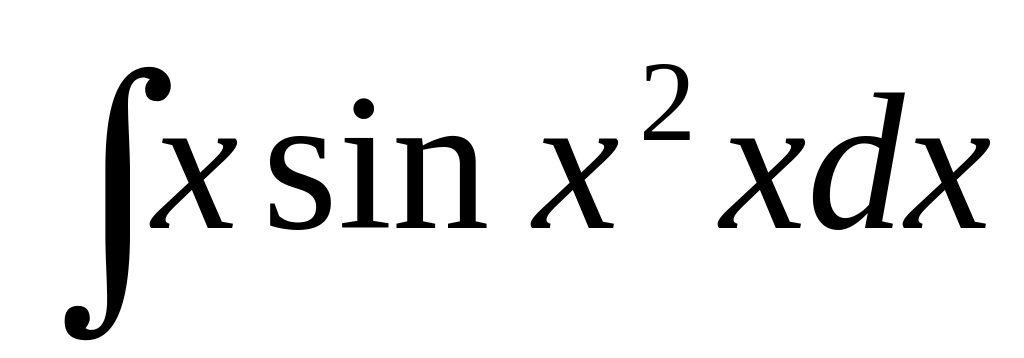
129
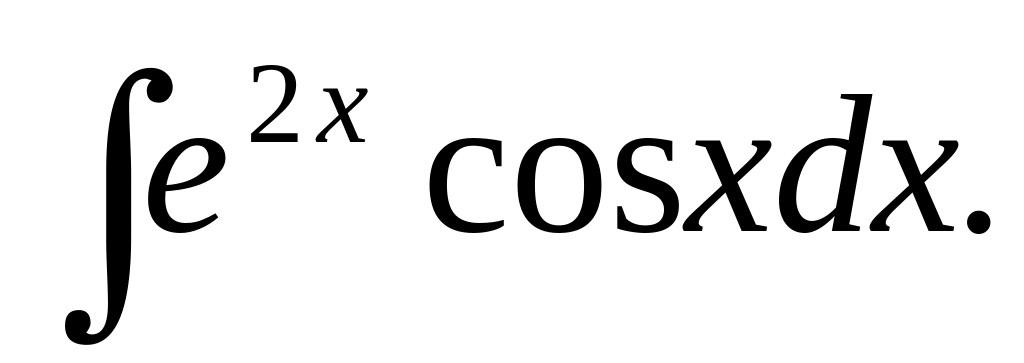
Пособие может быть использовано студентами для самостоятельного изучения соответствующего материала, выполнения практического занятия 16 Основные способы интегрирования и самостоятельной работы студента 16 Интегрирование функций: непосредственным способом, заменой переменной, по частям.
Данное учебно-методическое пособие является базовым для подготовке студентов к экзамену по модулю ЕН.01.М.07 Интегральное исчисление.
Работая с пособием, студенты имеют возможность одновременно обращаться к учебной и справочной литературе:
- Бермант, А.Ф. Краткий курс математического анализа: Учеб. Пособие/ Бермант А.Ф., Араманович И.Г. – 8-е изд., стер. – М.: Наука, 1973. – 720с.: ил.
Глава 5 Интеграл. Интегральное исчисление, §1 Неопределенный интеграл,
п.78-81;
- Подольский, В.А. Сборник задач по математике: Учеб. пособие/Подольский В.А., Суходский А.М., Мироненко Е.С. – 3-е изд., стер. – М.: Высш.шк., 2005. – 495 с.: ил.
Глава 12 Неопределенный интеграл, §1-§3.
1 Неопределенный интеграл
1.1 Понятие неопределенного интеграла
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции.
Разнообразные
вопросы математического анализа, его
многочисленные приложения в геометрии,
физике, химии приводят к решению обратной
задачи: по заданной функции
найти
такую функцию
,
производная которой была бы равна
функции
,
т.е. найти функцию
,
зная её производную
.
Обратную задачу решает интегральное исчисление.
Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.
Определение. Функция называется первообразной функции в данном интервале, если во всех точках этого интервала её производная равна заданной функции, т.е. .
Из определения вытекают три вопроса.
1 Любая ли функция имеет первообразную?
2 Если существует, то сколько первообразных может иметь заданная функция?
3 Как найти эти первообразные?
Ответы на эти вопросы дают теоремы.
Теорема 1 (без доказательства)
Если функция непрерывная в данном интервале, то она имеет первообразную.
Теорема 2 Всякая непрерывная функция имеет бесчисленное множество первообразных
Пусть
-
первообразная функции
,
тогда и функция
так
же является её первообразной. Действительно
:
Например,
первообразной функции
является функция
,
т.к.
Очевидно,
что первообразными будут также любые
функции
где С – постоянная, поскльку
Теорема 3 (без доказательства)
Любые две первообразные функции отличаются друг от друга постоянным слагаемым.
Определение
Неопределенным
интегралом
для
заданной функции
называется
совокупность всех её первообразных и
обозначается
.
Таким образом, по определению
(*)
В равенстве (*):
- подынтегральная функция (ПФ);
-
подынтегральное выражение (ПВ);
- первообразная функции;
- совокупность первообразных;
-
дифференциал независимой переменной,
указывает по какой переменно функция
интегрируется.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Интегрирование действие обратное дифференцированию и его можно проверить дифференцированием.
1.2 Свойства неопределённого интеграла
1.2.1 Производная неопределённого интеграла равна подынтегральной функции:
1.2.2 Дифференциал от неопределённого интеграла равен подынтегральному выражению:
1.2.3 Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
1.2.4 Постоянный множитель можно выносить за знак интеграла:
1.2.5 Неопределённый интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функции:
1. 3 Таблица основных интегралов
-
1
8
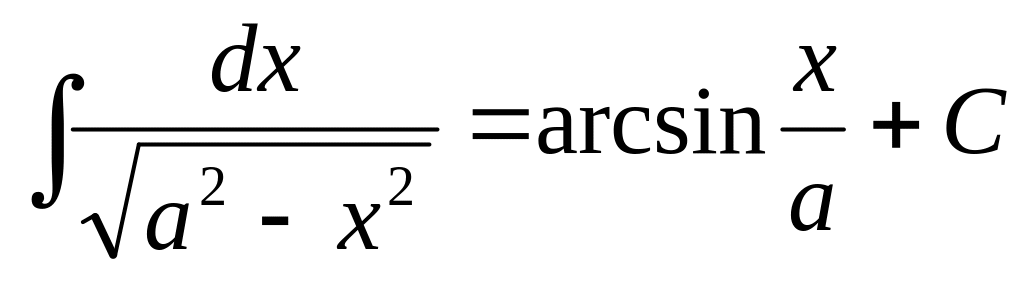
2
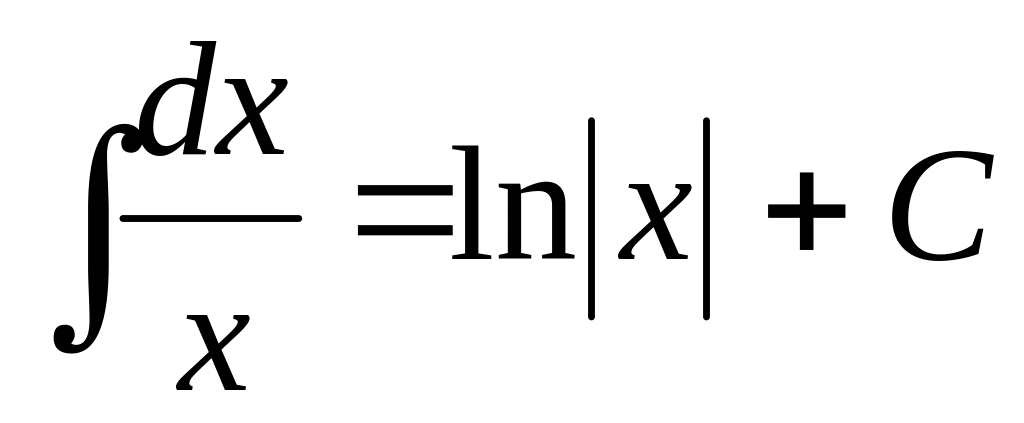
8.1
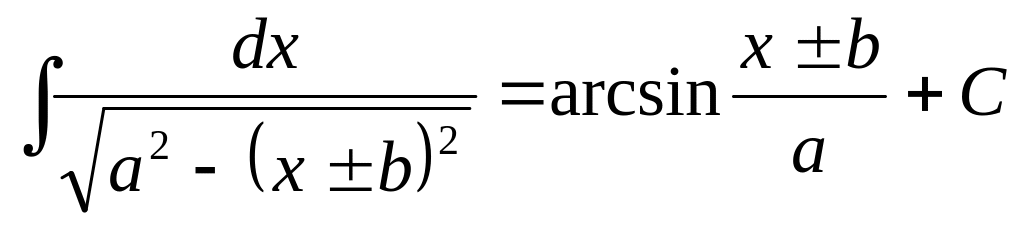
2.1
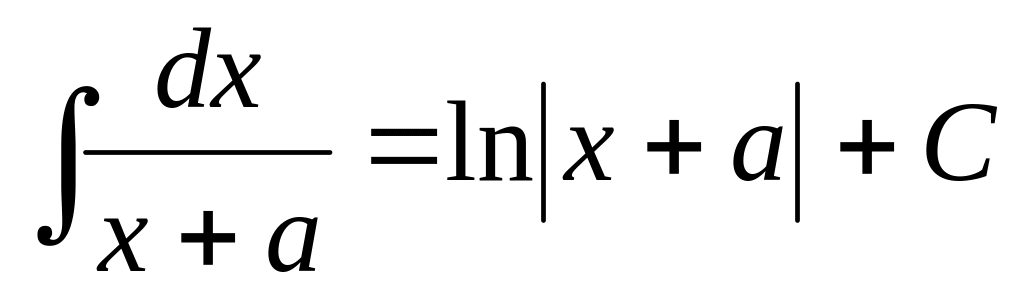
8.2
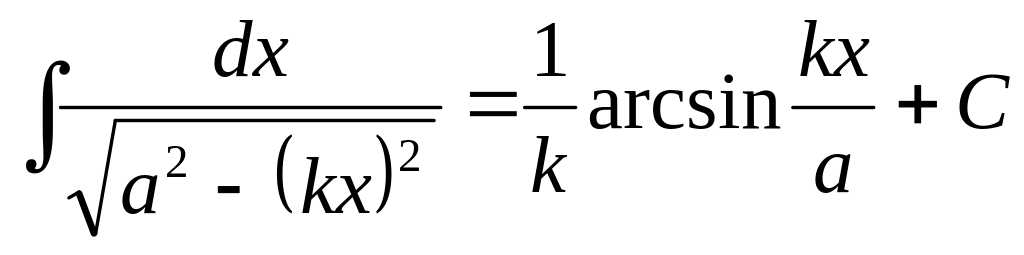
2.2
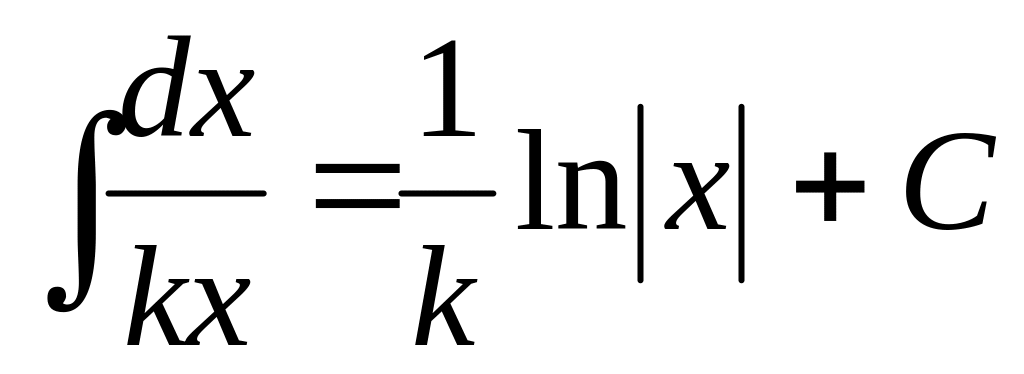
9
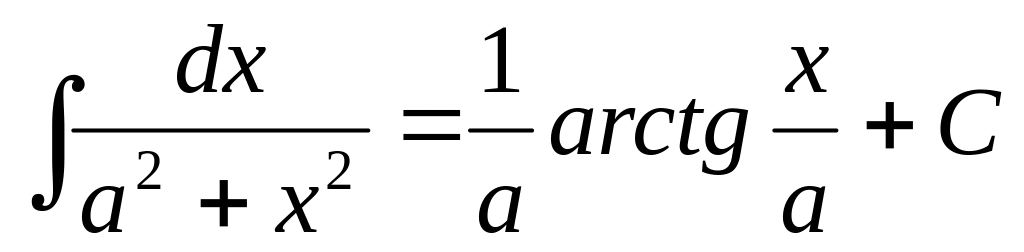
3
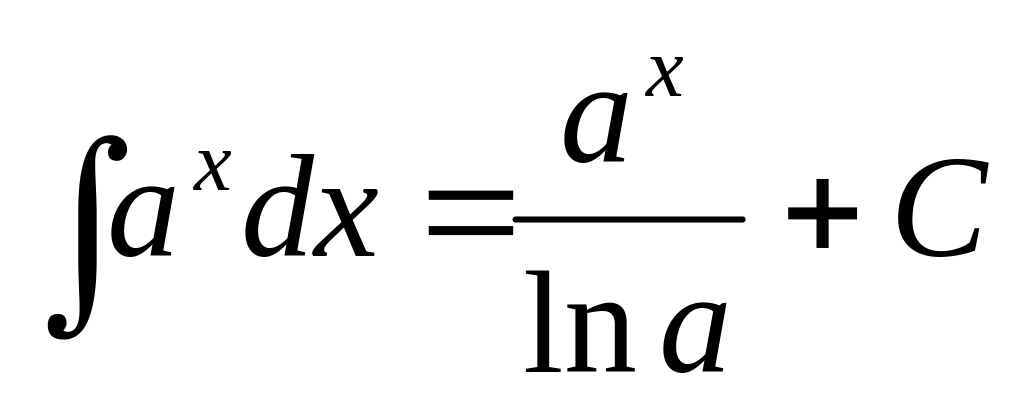
9.1
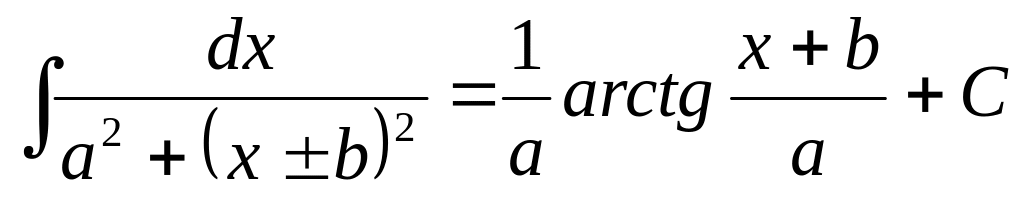
3.1
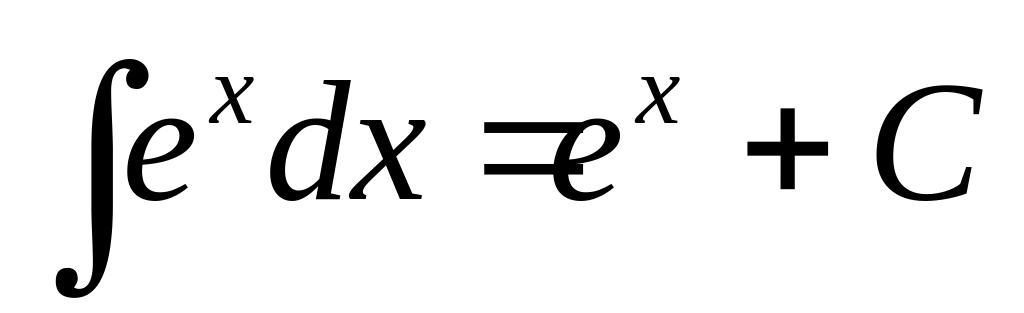
9.2
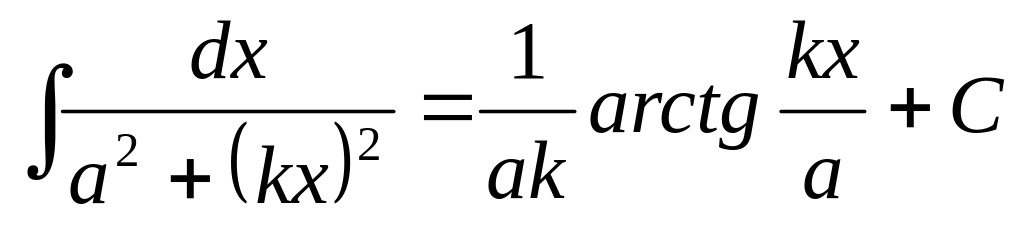
3.2
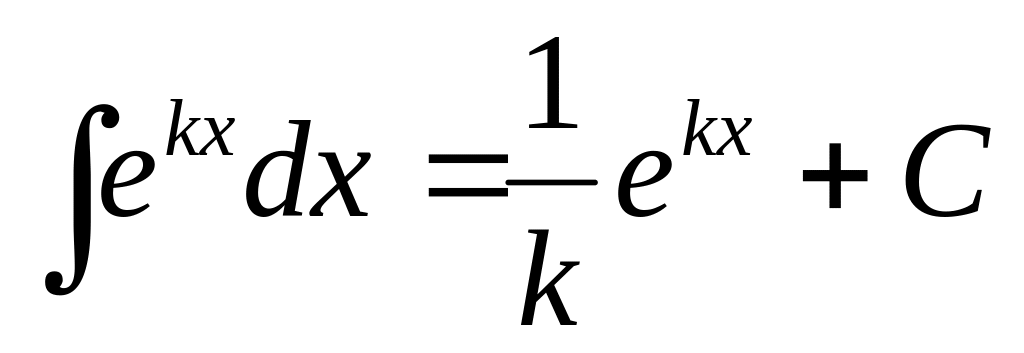
10
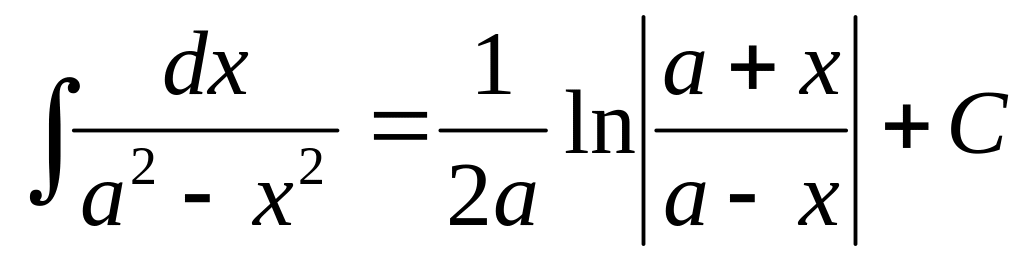
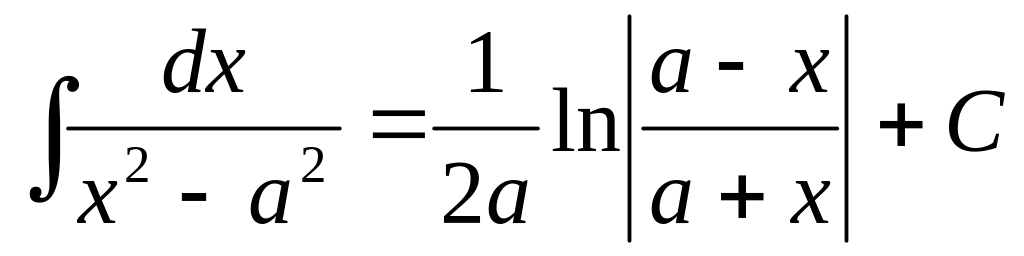
3.3
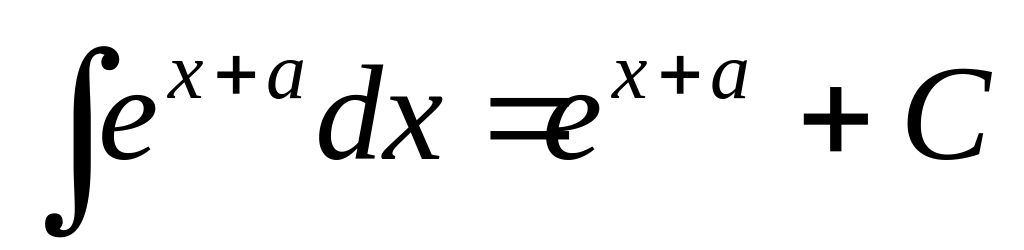
4
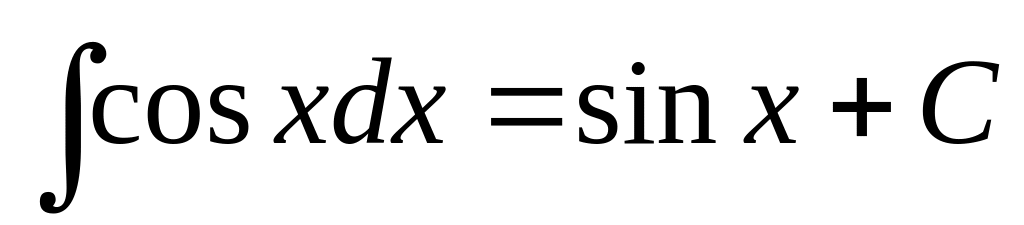
4.1
10.1
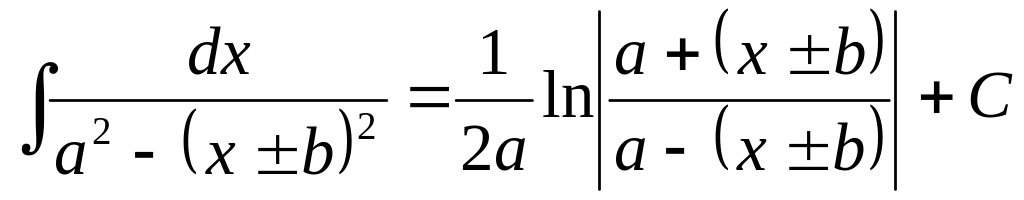
4.2
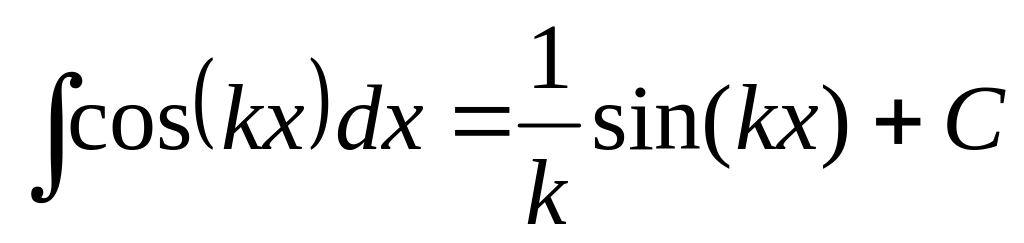
10.2
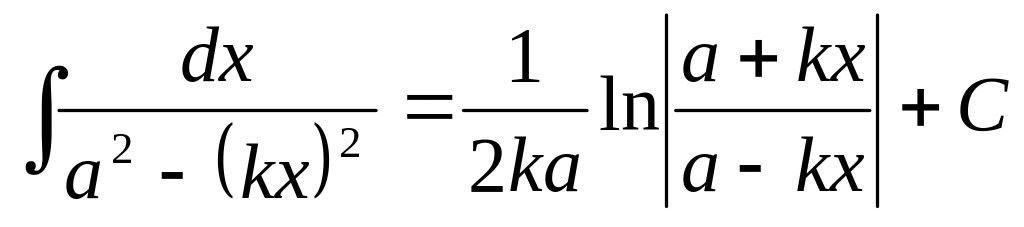
5
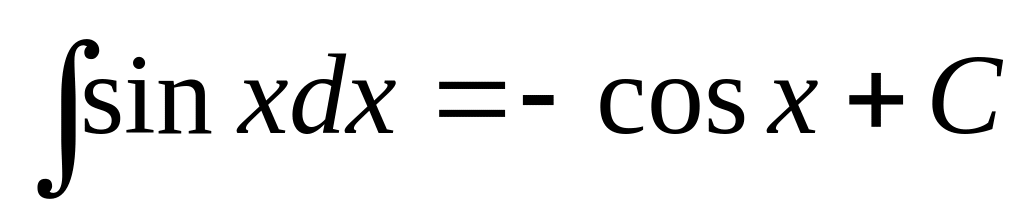
11
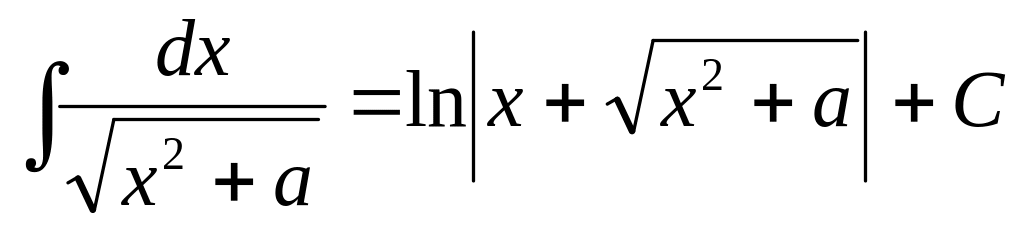
5.1
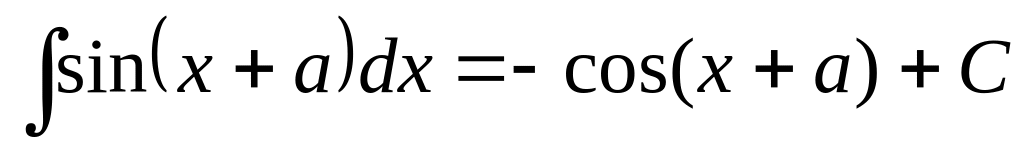
11.1
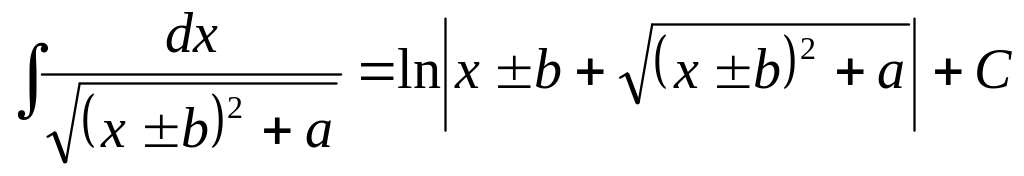
5.2
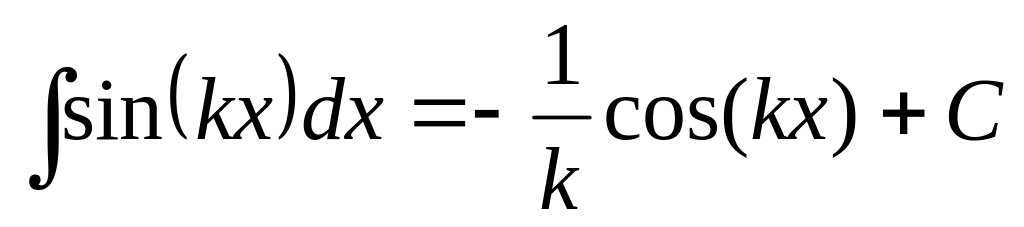
11.2
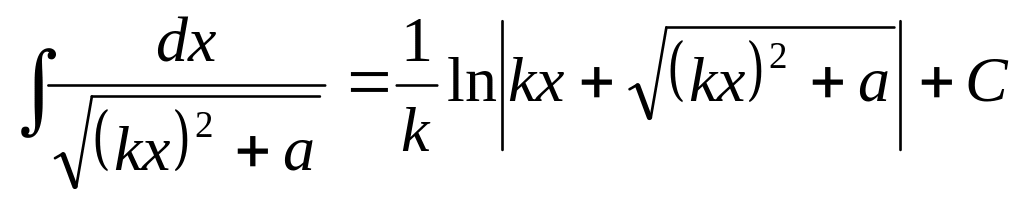
6
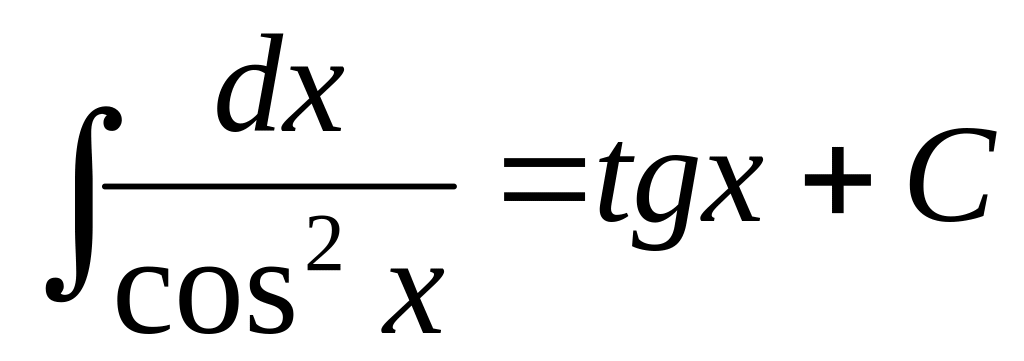
12
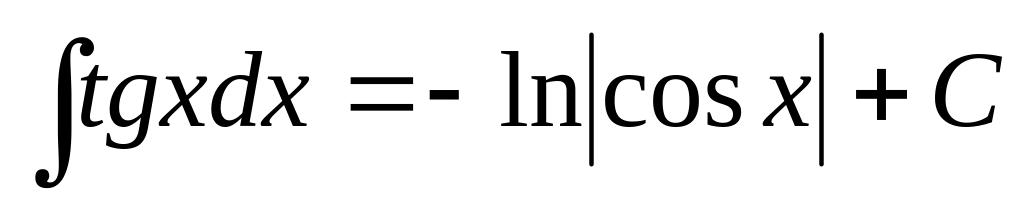
6.1
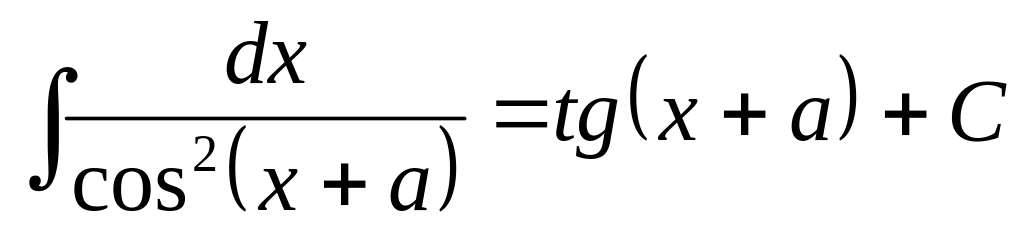
12.1
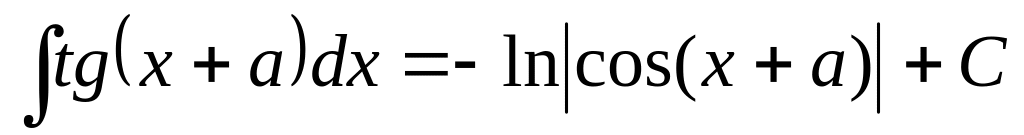
6.2
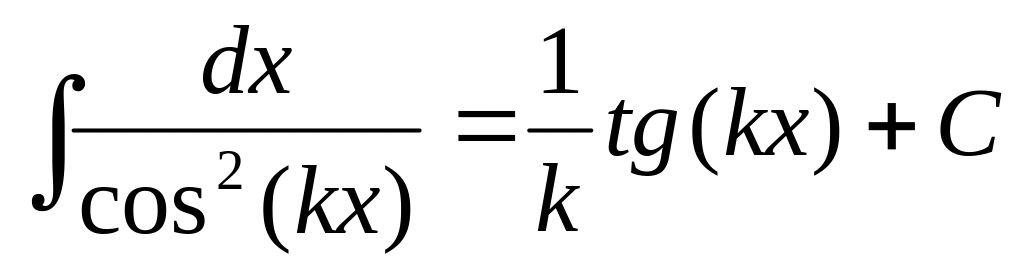
12.2
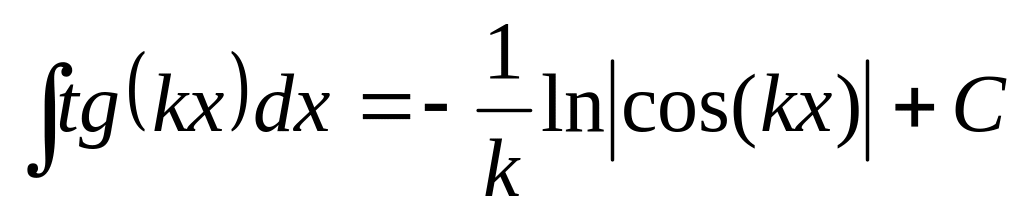
7
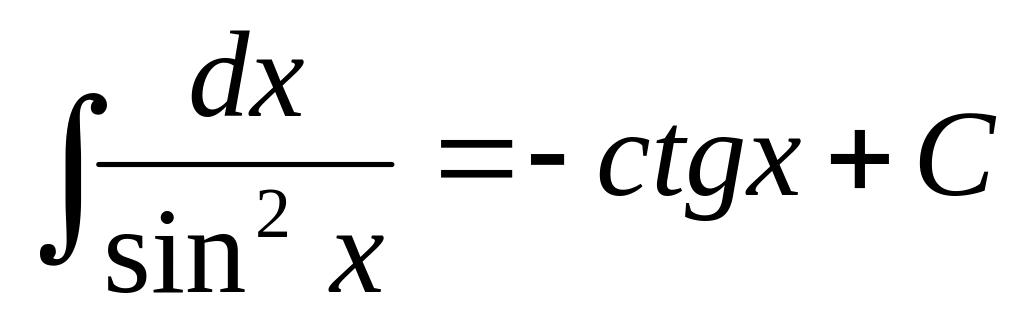
13
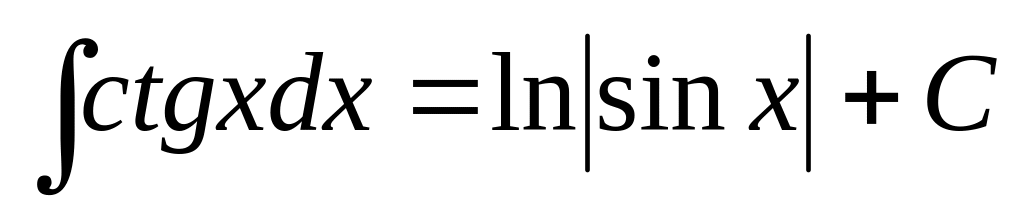
7.1
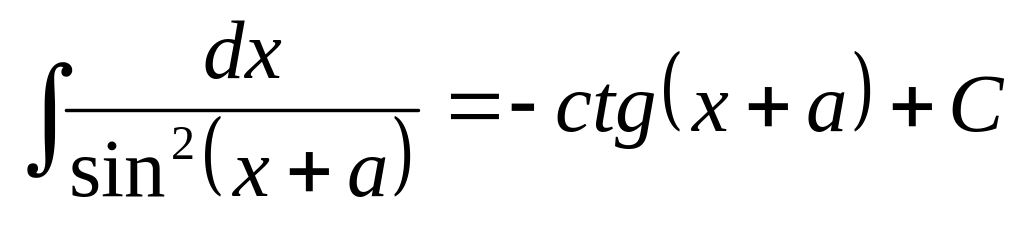
13.1
7.2
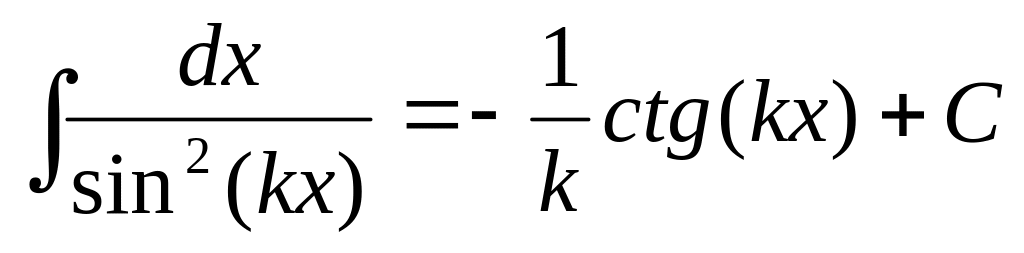
13.2
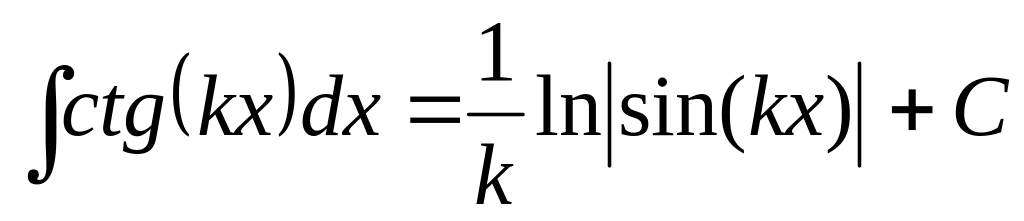
14
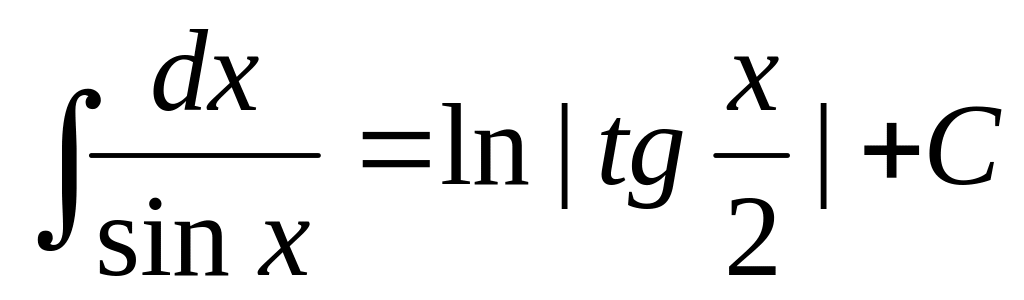
15
