Алгоритм заполнения с упорядоченным списком ребер

В компьютерной графике генерацию сплошных областей называют заполнением (закраской) многоугольников (контуров). Алгоритмы заполнения с упорядоченным списком ребер относятся к группе методов «растровой развертки». В таких алгоритмах для всех ребер многоугольника, за исключением горизонтальных, в произвольной последовательности определяются точки их пересечения с осями сканирующих строк, сдвинутыми по оси y на пол пикселя вверх относительно координат адресуемых точек соответствующих рядов пикселей. Следуя вдоль каждой сканирующей строки, имеющей такие пересечения, от ее начала к концу, сортируют точки пересечения попарно. Интервалы между точками пересечения, входящими в пары, заполняются цветом многоугольника. Для интервалов между этими парами пересечений и крайних (от начала строки до первого пересечения и от последнего пересечения до конца строки) используется фоновый цвет.

При задании многоугольника целочисленными координатами его вершин возможный вариант последовательности действий алгоритма заполнения с упорядоченным списком ребер такова:

• определить для каждого ребра многоугольника точки пересечений с осями сканирующих строк (горизонтальные ребра игнорировать); если ось сканирующей строки с вертикальной координатой y₀ пересекает ребро с вершинами P₁ (x₁ , y₁) и P₂ (x₂ , y₂), горизонтальная координата точки пересечения определяется по формуле ;

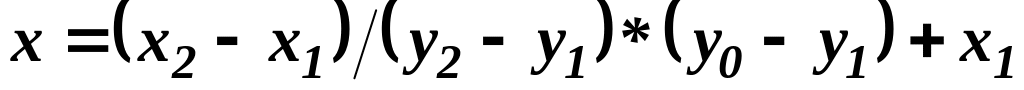• занести каждое пересечение (x, y + 0,5) в список;

• отсортировать список по строкам (сверху вниз) и по возрастанию x в строке – (x₁ , y₁) предшествует (x₂ , y₂), если y₁ > y₂ или y₁ = y₂ и x₁ < x₂ ;

• выделить из отсортированного списка пары элементов (x₁ , y₁) и (x₂ , y₂); при этом структура списка будет гарантировать, что в таких парах y₁ = y₂ и x₁ < x₂ ;

• заполнить на соответствующих сканирующих строках пиксели с горизонтальными координатами x адресуемых точек, удовлетворяющих условию x₁  x + 0,5  x₂ на каждом интервале (т.е. пиксели, центры которых попадают в интервалы между выделенными парами точек пересечения).

При работе подобного алгоритма по заполнению, например, приведенного на рис.3 пятиугольника на оси сканирующей строки y₀ = 3,5 будут выделены две пары точек: с x = 1,5 и x = 3,25; с x = 5 и x = 6,75. На самой сканирующей строке заполнятся пиксели с координатами адресуемых точек (1, 3), (2, 3), (5, 3) и (6, 3), т.к. для первых двух пикселей выполняется условие: 1,5  x + 0,5  3,25, а для вторых двух: 5  x + 0,5  6,75. Рис.3 иллюстрирует также полный результат работы алгоритма.

Д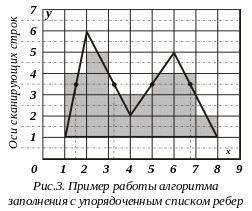 алее приведен возможный вариант такого алгоритма на псевдокоде (см. приложение 1). В нем используются следующие обозначения: M – число вершин многоугольника; Вершины – список целочисленных координат вершин; MinY и MaxY – наименьшая и наибольшая у-координаты вершин; у_min и у_max – наименьшая и наибольшая у-координаты обрабатываемого ребра; Пересечения – список, содержащий вещественные значения x точек пересечения ребер с осями сканирующих строк и соответствующие целочисленные значения y; N – общее число таких точек пересечения; Список – список x-координат точек пересечения на обрабатываемой строке, сортируемый в процессе обработки; x_лев и x_пр – левая и правая x-координаты интервала между парой точек пересечения, обрабатываемого в подпрограмме Интервал; Треб_знач – переменная, которая идентифицирует цвет заполняемого многоугольника.

Инициализация переменных

Вершины [M+1] = Вершины [1]

MinY = Вершины [1].y

MaxY = MinY

j = 0

Определение горизонтальных координат точек пересечения ребер с осями сканирующих строк; занесение их в список Пересечения вместе с целочисленными координатами y сканирующих строк; определение границ многоугольника по y

for i = 1 to M

if Вершины [i].y < > Вершины [i+1].y then

if Вершины [i].y < Вершины [i+1].y then

у_min = Вершины [i].y

у_max = Вершины [i+1].y

else

у_min = Вершины [i+1].y)

у_max = Вершины [i].y

end if

for y = у_min to у_max – 1

j = j + 1

Пересечения [ j].x = (Вершины [i+1].x – Вершины [i].x) /

(Вершины [i+1].y – Вершины [i].y) *

( y + 0.5 – Вершины [i].y) + Вершины [i].x

Пересечения [ j].y = y

if MinY > у_min then MinY = у_min

if MaxY < у_max then MaxY = у_max

next y

end if

next i

N = j

Получили список Пересечения всех точек пересечения (значения x – вещественные, y – целые); число элементов – N

Построчная обработка точек пересечения с сортировкой их по x и заполнением интервалов между парами пересечений

for y = MaxY – 1 to MinY step –1

j = 0

for i = 1 to N

if Пересечения [i].y = y then

j = j + 1

Список [ j].x = Пересечения [i].x

end if

if j = 1 go to 1

k = j

while (Список [k].x < Список [k–1].x)

Врем = Список [k].x

Список [k].x = Список [k–1].x

Список [k–1].x = Врем

k = k – 1

if k = 1 go to 1

end while

1 next i

Получили список x-координат точек пересечения в текущей строке с сортировкой по возрастанию; выходное значение j – число пересечений

Заполнение интервалов между парами пересечений

for i = 1 to j – 1 step 2

call Интервал (Список [i].x, Список [i+1].x, y)

next i

next y

finish

Подпрограмма заполнения интервала между парой точек пересечения

subroutine Интервал (x_лев , x_пр , y)

Определение x-координаты самого левого пикселя в строке, удовлетворяющего условию x_лев  x + 0.5

x = Integer (x_лев + 0.5)

if x = x_лев + 0.5 then x = x – 1

while (x + 0.5  x_пр)

Пиксель (x, y) = Треб_знач

x = x + 1

end while

return