1.5.1. Формулировка граничных условий

1. Нормальная составляющая вектора электрической индук­ции на границе раздела сред терпит разрыв, равный поверхност­ной плотности электрического заряда.

При отсутствии поверхностных зарядов нормальная состав­ляющая вектора электрической индукции непрерывна: .

2. Нормальная составляющая вектора магнитной индукции на границе раздела сред всегда непрерывна: . этот факт связан с тем, что в природе не существует свободных магнитных зарядов.

3. Тангенциальная составляющая напряженности электричес­кого поля на границе раздела сред всегда непрерывна: .

4. Тангенциальная составляющая напряженности магнитного поля на границе раздела сред терпит разрыв, величина которого определяется поверхностной плотностью электрического тока (рис. 1.2).

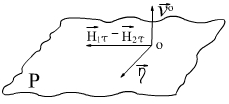
Рис. 1.2

Связь и на границе раздела сред

При отсутствии поверхностных токов тангенциальная сос­тавляющая напряженности магнитного поля на границе раздела сред непрерывна: Заметим, что поверхностные токи могут быть только на поверхности идеального проводника.

1.5.2. Граничные условия для переменного электромагнитного поля на поверхности идеального проводника

Из уравнений Максвелла следует, что все характеристики

переменного электромагнитного поля в идеальном проводнике рав­ны нулю.

Действительно, из третьего уравнения (1.14 а) следует, что при

напряженность электрического поля в проводнике .

Из второго уравнения системы (1.6) следует, что . Отсюда для переменного поля находим, что и .

Далее, из первого и второго уравнений (1.14а) очевидно, что и .

Полагая в общих граничных условиях характеристики поля в области II равными нулю, получим на поверхности идеального про­водника:

1. ; 2. ; 3. ; 4. . (1.23)

Таким образом, на поверхности идеального проводника тан­генциальные составляющие напряженности и индукции электричес­кого поля и нормальные составляющие индукции и напряженности магнитного поля равны нулю.

При исследовании электромагнитных полей вблизи металлических тел, удельная проводимость которых [См/м], с вы­сокой степенью точности можно считать металлическое тело иде­альным проводником, а на его поверхности использовать гранич­ные условия (1.23).

1.6. Теорема Пойнтинга

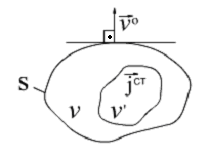
Рис.1.3

Сторонние источники в произвольной области

Рассмотрим произвольную область , ограниченную поверхностью S, в которой могут находиться источники поля, харак­теризуемые объемной плотностью тока (рис.l.3).

Из уравнений электродинамики (1.18) может быть получена основная теорема теории электромагнитного поля - теорема Пойнтинга.

, (1.24)

где - энергия электромагнитного поля, запасенная в области ;

Р - полная мощность, которую можно представить в виде:

, (1.24а)

где - мгновенная мощность, вырабатываемая источниками;

- мгновенная мощность, расходуемая на нагрев среды в области V;

-мгновенная мощность, проходящая через по­верхность S;

- вектор Пойнтинга, представляющий плотность потока мощности через единичную площадку поверхности S .

Если полная мощность Р = О, то энергия электромагнитного поля в области остается постоянной.

Из (1.24) и (1.24а) следует, что величина электромагнит­ной энергии в области V может измениться в силу ряда причин:

1) за счет действия источников она возрастает:

и .

2) за счет нагрева среды она уменьшается:

и

3) за счет излучения из области , когда , она уменьшается:

.

4) за счет притока энергии извне, когда возрастает: