1.2.2. Уравнение непрерывности и закон сохранения заряда

Возьмем дивергенцию от обеих частей первого уравнения (1.6). Учитывая, , получаем:

. (1.11)

Это уравнение называется уравнением непрерывности. Оно отражает тот факт, что силовые линии вектора , пред­ставляющего сумму плотностей токов смещения и проводимости, непрерывны.

Перепишем уравнение (1.11) в виде . Используя третье уравнение Максвелла из (1.6), получаем:

. (1.12)

Это уравнение выражает закон сохранения заряда в диффе­ренциальной форме.

Интегрируя уравнение (1.12) по произвольной области V и принимая во

внимание, что , получим соотношение

, (1.13)

которое выражает закон сохранения заряда в интегральной форме:

величина заряда в области может измениться только за счет его вытекания из этой области, или за счет его притока извне. При отсутствии движения зарядов ( ) величина заряда в области остается постоянной.

1.3. Материальные уравнения и классификация сред

Система уравнений Максвелла (1.6) в математическом смыс­ле не является полной. Первое и второе уравнения этой системы включают пять неизвестных функций. Неполнота системы (1.6) объясняется ее универсальностью: уравнения Максвелла описывают электромагнитные процессы в любых средах, в то время как пара­метры, характеризующие среду, в них отсутствуют.

В зависимости от вида среды функциональная связь между векторами описывается материальными уравнениями:

.

В общем случае для произвольной среды материальные урав­нения можно записать в следующем виде:

, (1.14)

где - квадратные матрицы третьего порядка (тензоры). Элементы этих матриц представляют собой параметры, характеризующие произвольную среду. Материальное уравнение -в координатной форме записывается в виде:

,

,

,

где тензор диэлектрической проницаемости имеет вид:

.

Аналогично записываются и два другие материальные урав­нения и тензоры .

Таким образом, произвольная среда может быть описана 27 параметрами.

Если все параметры среды не зависят от векторов поля, то такая среда называется линейной. Если хотя бы один из парамет­ров зависит от векторов поля, то среда называется нелинейной.

Если все параметры среды не зависят от координат, то та­кая среда называется однородной. Если хотя бы один из парамет­ров зависит от координат, то среда называется неоднородной.

Среда, свойства которой не зависят от направления в пространстве, называется изотропной средой. В изотропной среде вектор параллелен вектору , вектор параллелен вектору , а вектор параллелен вектору .

Для анизотропной среды нарушается условие параллельности векторов и , или и , или и .

Для изотропной линейной среды материальные уравнения записываются в виде:

, (1.14а)

где - скалярные величины, не зависящие от векто­ров поля.

Таким образом, изотропная линейная среда характеризуется только тремя параметрами:

- абсолютная диэлектрическая проницаемость среды, имеющая размерность Ф/м (Фарада на метр) ; - абсолютная магнитная проницаемость среды, имеющая размерность Гн/м (Генри на метр);

- удельная проводимость среды, имеющая размерность 1/(Ом*м) = См/м (Сименсна метр).

Часто среды характеризуют относительными проницаемостями, сопоставляя их абсолютные проницаемости с проницаемостями вакуума:

- относительная диэлектрическая проницаемость среды;

- относительная магнитная проницаемость среды.

В зависимости от величины среды делят на проводники, диэлектрики и среды, занимающие промежуточное положение между проводниками и диэлектриками.

Среда, у которой = 0, называется идеальным диэлектри­ком, а у которой -идеальным проводником.

В идеальном проводнике могут существовать только токи проводимости с плотностью . При этом напряженность электрического поля в идеальном проводнике равна нулю. Поэтому в идеальном проводнике отсутствуют токи смещения:

.

В идеальном диэлектрике, наоборот, могут существовать лишь токи смещения, а токи проводимости отсутствуют.

В реальных средах могут существовать как токи проводи­мости, так и токи смещения. Если в среде преобладают токи про­водимости, то ее относят к проводнику, а если преобладают то­ки смещения, то к диэлектрику.

Рассмотрим электромагнитное поле в линейной изотропной среде, вектор которого в каждой точке среды изменяется по за­кону гармонических колебаний:

, (1.15)

где - круговая частота колебаний.

Определим плотности тока проводимости и тока смещения : ,

.

Рассмотрим отношение амплитуд этих токов, которое назы­вают тангенсом угла диэлектрических потерь _:

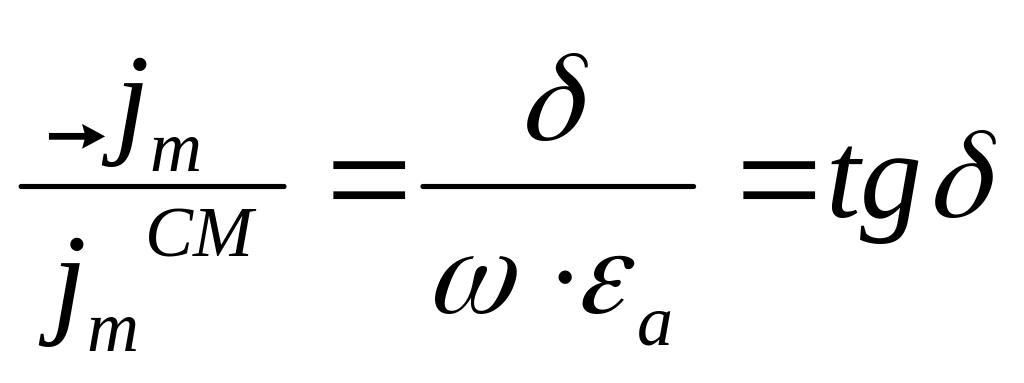. (1.16)

При <<1 среду относят к диэлектрику, а при >>1- к проводнику.

Для металлических проводников, у которых [См/м], во всем диапазоне радиочастот >>1. Поэтому все металлы являют­ся хорошими проводниками.

Электропроводность материалов, использующихся в радиотехнике в качестве диэлектриков, имеет порядок [СМ/м]. Для этих сред <<1.

Среды, у которых на низких частотах >>1, а на высоких <<1 (например, земная почва), относят к средам, занимающим промежуточное положение между проводниками и диэлектриками.