2.6.4 Диаграмма направленности

Диаграмма направленности – это характеристика излучателя, показывающая зависимость амплитуды поля в дальней зоне от направления в пространстве (от углов и ).

Диаграмма направленности в меридиональной плоскости (МП)

Меридиональная плоскость – это плоскость, проходящая через ось z. Уравнение этой плоскости в сферических координатах записывается в виде:

, ,где (2.62)

Диаграмма направленности в меридиональной плоскости представляет кривую, задаваемую уравнением:

(2.63)

где r – длина радиус-вектора, проведённого в меридиональной плоскости из начала координат под углом к оси z;

- амплитуда напряжённости электрического поля в дальней зоне;

-максимальное значение амплитуды.

Диаграмма направленности элементарного электраческого излучателя в меридиальной плоскости представляет собой две окружности, касающиеся оси z в начале координат (рис. 2.7).

Рис.2.7. Диаграмма направленности в МП

Диаграмма направленности в эквивалентной плоскости (ЭП)

Эквивалентная плоскость – это плоскость, проходящая через начало координат перпендикулярно оси z. Уравнение этой

плоскости в сферических координатах записывается в виде: .

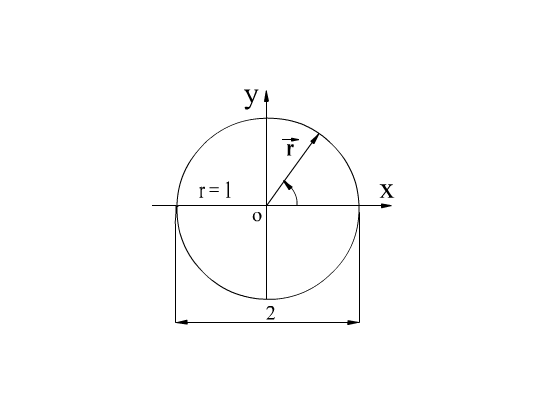
Диаграмма направленности элементарного электраческого излучателя в экваториальной плоскости представляет собой кривую, задаваемую уравнением:

, (2.64)

где - длина радиуса-вектора, проведённого в эквивалентной плоскости из начала координат под углом к плоскости x.

Так как амплитуда волны не зависит от угла , то диаграмма направленности представляет собой окружность с центром.

Диаграмма направленности в ЭП в начале координат (рис. 2.8.).

Рис.2.8. Диаграмма направленности в ЭП.

Пространственная диаграма направленности

В произвольной точке пространства в дальней зоне амплитуда поля зависит от обеих координат и , и пространственная диаграмма направленности представляет собой поверхность (рис. 2.9.), задаваемую уравнением :

, (2.65)

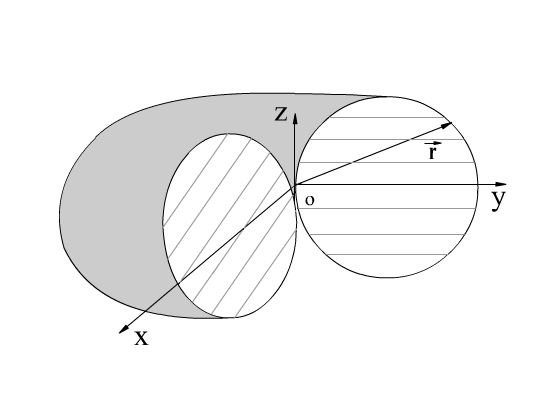
Рис.2.9. Пространственная диаграмма направленности.

Диаграмма направленности строится следующим образом. В заданном направлении, определяемом углами и , проводиться радиус-вектор - и на нём откладывается отрезок, длина которого пропорциональна амплитуде поля в данном направлении.

При изменении углов и в пределах конец радиус-вектора описывает поверхность, задаваемую уравнением (2.65).

Пространственная диаграмма направленности элементарного электрического излучателя представляет собой поверхность тора, образованную вращением окружности, соприкасающейся в начале координат с осью z, вокруг этой оси.

2.6.5. Мощность и сопротивление излучения

Излучаемую мощность можно найти, используя уравнение энергетического баланса (1.31) и полагая в нём (удельная проводимость среды ) и

(2.66)

где среднее значение вектора Пойтинга

(2.67)

а S – замкнутая поверхность, ограничивающая область, в которой расположен излучатель. При этом величина не зависит от формы и размеров поверхности S.

В качестве поверхности S удобно выбрать сферу с центром в начале координат, радиус которой стремиться к бесконечности. В этом случае выражение (2.66) для излучаемой мощности приводиться к виду:

(2.68)

При вычислении по формуле (2.67) используем выражения (2.55) для поля в дальней зоне:

(2.69)

Подставляя (2.69) в (2.68) и интригуя, получим следующее выражение для :

(2.70)

или (2.71)

где множитель (2.72)

называется сопротивлением излучения элементарного электрического излучателя. По величине можно судить об эффективности излучения. Чем больше , тем больше излучаемая мощность при заданной амплитуде тока . Эффективность излучения повышается с ростом частоты и увеличением длины излучателя.