
- •Часть 1. Основы теории электромагнитного поля
- •Часть I. Основы теории электромагнитного поля
- •Часть 1. Основы теории электромагнитного поля: Учеб.Пособие/ Моск. Гос. Ин-т
- •Часть 1. Основы теории электромагнитного поля
- •Глава 1. Основные понятия и уравнения электродинамики
- •1.2. Уравнения Максвелла
- •1.2.2. Уравнение непрерывности и закон сохранения заряда
- •1.3. Материальные уравнения и классификация сред
- •1.4. Полная система уравнений электродинамики
- •1.5. Граничные условия электродинамики
- •1.5.1. Формулировка граничных условий
- •1.6. Теорема Пойнтинга
- •1.6. Теорема Пойтинга
- •1.7. Уравнения электродинамики и теорема Пойнтинга
- •1.8. Теорема единственности для внутренних и внешних задач электродинамики
- •1.8.1. Внутренняя задача
- •1.8.2. Внешняя задача
- •Доказательство
- •Глава 2. Возбуждение электромагнитных волн в свободном пространстве
- •2.1. Постановка задачи
- •2.2. Волновые уравнения электродинамики Векторный потенциал
- •2.3. Векторный потенциал элемента электрического тока
- •2.4. Векторный потенциал линейного, поверхностного и объемного токов
- •2.5. Электромагнитное поле поверхностного тока, равномерно распределенного на бесконечной плоскости. Плоские однородные волны (пов)
- •2.5.1. Основные характеристики пов
- •2.5.2. Пов с линейной, круговой и эллиптической поляризацией векторов поля.
- •Волна с левой круговой поляризацией определяется выражениями (2.43), (2.44) при .При этом . (2.47)
- •2.6. Электромагнитное поле элементарного
- •2.6.1. Векторный потенциал
- •2.6.2. Напряжённость поля
- •2.6.3. Электромагнитное поле в дальней зоне
- •2.6.4 Диаграмма направленности
- •Меридиональная плоскость – это плоскость, проходящая через ось z. Уравнение этой плоскости в сферических координатах записывается в виде:
- •Диаграмма направленности в меридиональной плоскости представляет кривую, задаваемую уравнением:
- •Пространственная диаграма направленности
- •2.6.5. Мощность и сопротивление излучения
- •Глава 3. Основные принципы теории электромагнитного поля
- •3.1. Принцип суперпозиции
- •Если объёмную плотность стороннего тока
- •3.2. Принцип излучения на бесконечности
- •3.3. Принцип взаимности
- •3.4.1. Электромагнитное поле элементарного магнитного излучателя.
- •3.4.2. Электромагнитное поле элементарного щелевого излучателя.
- •3.5. Принцип эквивалентности
- •3.5.1. Электромагнитное поле элемента Гюйгенса.
- •Часть 1. Основы теории электромагнитного поля...............................5
- •Глава 1. Основные понятия и уравнения электродинамики............................…………………………………....5
- •Глава 2. Возбуждение электромагнитных волн в свободном пространстве.....................…………………………………………….26
- •Глава 3. Основные принципы теории электромагнитного поля……………………………………………………........................49
- •Александр Николаевич Коваленко
- •Часть 1. Основные теории электромагнитного поля
2.6.2. Напряжённость поля
Напряжённость
электрического поля находим, используя
формулу (2.7)
![]() и представление
и представление
![]() в сферической системе координат (
в сферической системе координат (![]() ):
):
 ,
(2.51)
,
(2.51)
где
![]() -
орты сферической системы координат
(рис. 2.6).
-
орты сферической системы координат
(рис. 2.6).
Векторный
потенциал представляем в виде разложения
по этим ортам: ![]() , (2.52)
, (2.52)
где
![]() ;
;
![]()
Раскрывая определитель (2.51) по элементам первой строки, получим следующее выражение для комплексной амплитуды напряжённости магнитного поля:
![]() (2.53)
(2.53)
Используя
первое уравнение электродинамики для
комплексных амплитуд (1.28), можно получить
следующее выражение для комплексной
амплитуды напряжённости электрического
поля:
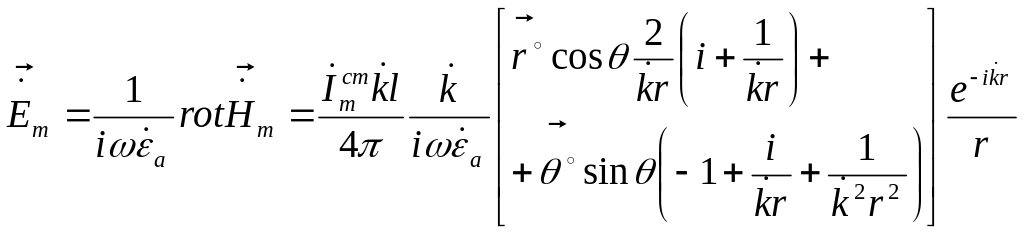 .
(2.54)
.
(2.54)
В зависимости от величины параметра
![]()
![]() всё пространство делят на три области:
всё пространство делят на три области:
1)
область пространства, для которой
![]() (
(![]() ),
),
называется дальней зоной (Д.З.);
2)
область пространства, для которой
![]() (
(![]() ),
),
называется ближней зоной (Б.З.);
3) остальная часть пространства называется промежуточной зоной (П.З.).
Наиболее сложную структуру поле имеет в промежуточной зоне. Для расчёта поля в этой области используются формулы (2.53), (2.54).
Для расчёта в Б.З. и Д.З. можно получить более простые формулы. Набольший практический интерес представляет поле в дальней зоне.
2.6.3. Электромагнитное поле в дальней зоне
Сферическая волна
При
расчёте поля Д.З. в общих выражениях
(2.53), (2.54) можно оставить лишь те члены,
которые при
![]() убывает как
убывает как
![]() .
В результате получим следующие выражения
для комплексных амплитуд поля:
.
В результате получим следующие выражения
для комплексных амплитуд поля:
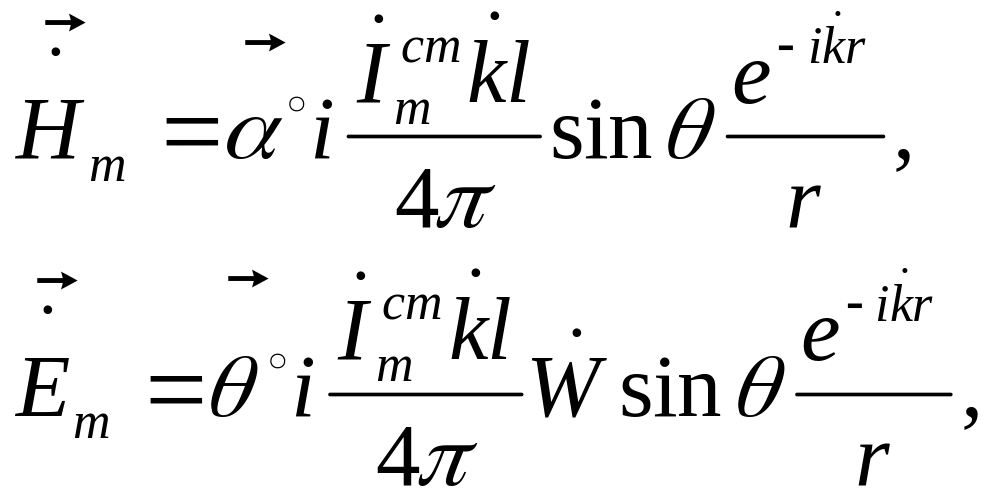 (2.55)
(2.55)
где
![]() -волновое
сопротивление среды.
-волновое
сопротивление среды.
Электромагнитное
поле, напряжённость которого определяется
выражениями (2.55), представляет собой
сферическую электромагнитную волну,
распространяющуюся в радиальных
направлениях от излучателя, расположенного
в начале координат. При этом векторы
и
![]() у сферической волны связаны между собой
такими же соотношениями, как и для
плоской однородной волны:
у сферической волны связаны между собой
такими же соотношениями, как и для
плоской однородной волны:
![]() (2.56)
(2.56)
где
![]() -
единичный вектор, указывающий направление
распространения волны.
-
единичный вектор, указывающий направление
распространения волны.
Запишем выражения для мгновенных значений векторов и :
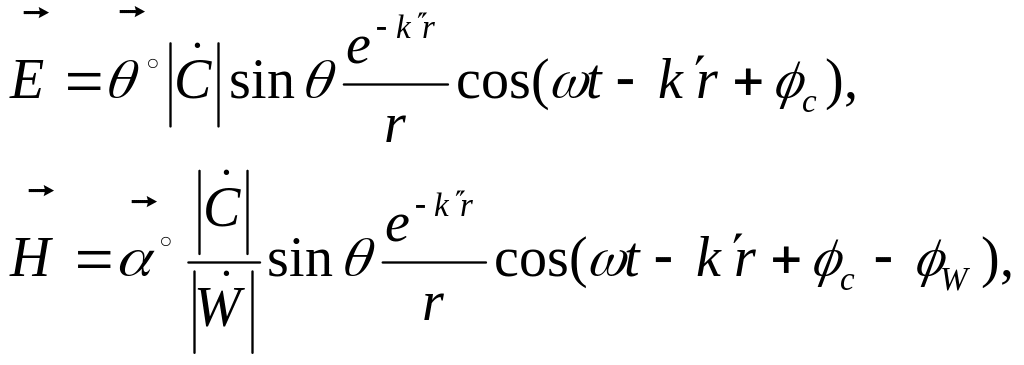 (2.57)
(2.57)
где
![]()
Основные характеристики сферической волны
Они определяются так же, как и для ПОВ.
Амплитуда волны - максимальное значение напряжённости электрического и магнитного полей (
 и
и
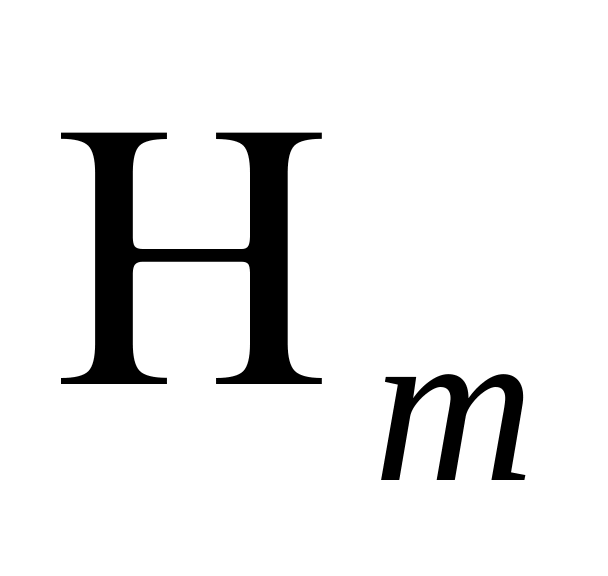 ):
):
![]()
![]() (2.58)
(2.58)
Фаза волны – аргумент косинусоидальной функции:
![]()
![]() (2.59)
(2.59)
Фронт волны – сферическая поверхность
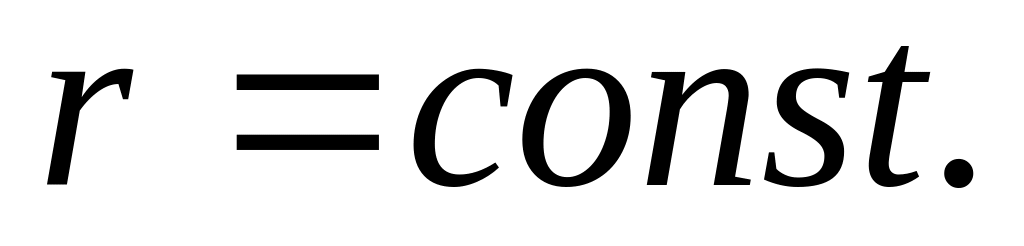
Фазовая скорость рассчитывается по формуле (2.38):
![]() (2.60)
(2.60)
Длина волны – рассчитывается по формуле (2.40):
![]() (2.61)
(2.61)
Из
выражения (2.58) видно, что амплитуда волны
зависит от расстояния
![]() и от угла
и от угла
![]() .
При отсутствии поглощения, т.е. при
.
При отсутствии поглощения, т.е. при
![]() амплитуда
волны изменяется обратно пропорционально
расстоянию
.
если амплитуда волны зависит от поперечных
координат
или
,
то волна называется неоднородной.
амплитуда
волны изменяется обратно пропорционально
расстоянию
.
если амплитуда волны зависит от поперечных
координат
или
,
то волна называется неоднородной.
Если амплитуда волны не зависит от азимутального угла , то такая волна называется азимутально однородной.
