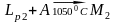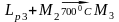ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МАТИ» - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ имени К.Э. ЦИОЛКОВСКОГО

Кафедра «Материаловедение и технология обработки материалов»

РАССЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине «Современные проблемы науки в области материаловедения и технологии материалов и покрытий»

на тему: «Анализ фазовых равновесий в трехкомпонентной системе с промежуточными конгруэнтно плавящимся и тремя инконгруэнтно плавящимися фазами».

Вариант №

Выполнил: Егенмамедов Х.О.

Группа: 4МТМ – 5ДМ – 093

Проверил: Осинцев О.Е.

Москва, 2012г.

СОДЕРЖАНИЕ:

Задание……………………………………………..……………………………

1.	Построение диаграммы состояния тройной системы А–В–С…………... Анализ граничных двойных систем А-В, В-С и А-С………….......... Анализ фазовых равновесий в трёхкомпонентной системе с промежуточными одной конгруэнтно плавящейся и тремя инконгруэнтно плавящимися фазами…………………………………
2.	Составление структурной схемы фазовых равновесий в трёхкомпонентной системе………………………………………………...
3.	Проекция поверхностей ликвидуса. Нанесение изотерм на поверхности ликвидуса в трёхкомпонентной системе………………….
4. 5. 6.	Построение изотермических разрезов………………………………….. 4.1. Построение изотермического разреза при комнатной температуре без растворимости в твёрдом состоянии………….….. 4.2. Построение изотермического разреза при комнатной температуре с растворимостью компонентов друг в друге и в промежуточных фазах ………………………………….…………… 4.3. Построение изотермического разреза при Т=640ºС………………… Построение политермических разрезов………………………………….. 5.1. Политермический разрез I–А …………………………………,...…… 5.2. Политермический разрез II–II………………………………………... Фазовые превращения в сплавах………………...………………………... 6.1. Сплав 1 (42%А, 3%В, 55%С)…………………………………… 6.2. Сплав 2 (47%А, 46%В, 7%С)………… …………………………….
	Список используемой литературы………………………………………...

1 Построение диаграммы состояния а-в-с

Построение диаграммы состояния системы А-В-С начинаем с анализа граничных двойных систем.

1.1 Анализ граничных двойных систем

Согласно заданию, в двойных системах существуют следующие фазы:

Система А-В:

L – жидкий раствор компонентов А и В друг в друге;

А – однокомпонентная твердая фаза;

В – однокомпонентная твердая фаза;

М₁ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава;

Система В-С:

L – жидкий раствор компонентов В и С друг в друге;

В – однокомпонентная твердая фаза;

С – однокомпонентная твердая фаза;

S₁ – промежуточная конгруэнтно плавящаяся фаза постоянного состава;

Система А-С:

L – жидкий раствор компонентов А и С друг в друге;

А – однокомпонентная твердая фаза;

С – однокомпонентная твердая фаза;

М₂ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава;

М₃ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава;

По этим данным строим диаграммы состояния систем А-В, В-С и А-С во всех возможных вариантах последовательности нонвариантных реакций, изображенных на рис. 1. Для каждой граничной двойной системы выбираем один вариант:

- для системы А-В – из двух возможных вариантов выбираем вариант “а”;

- для системы В-С – единственно возможный вариант “в” ;

- для системы А-С – из трех возможных вариантов выбираем вариант “е”.

В двойных системах существуют следующие нонвариантные равновесия:

В системе А-В:

- перитектическая реакция ;

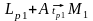- эвтектическая реакция .

В системе В-С:

- эвтектическая реакция .

- эвтектическая реакция .

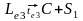В системе А-С:

- перитектическая реакция ;

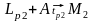- перитектическая реакция ;

- эвтектическая реакция .

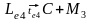1.2 Анализ фазовых равновесий в трехкомпонентной системе с промежуточными одной конгруэнтно плавящейся и тремя инконгруэнтно плавящимися фазами

В тройной системе А–В–С существуют 8 фаз:

1. L – жидкий раствор компонентов А, В, С друг в друге;

2. А – однокомпонентная твёрдая фаза;

3. В – однокомпонентная твёрдая фаза;

4. С – однокомпонентная твёрдая фаза;

5. S₁ – промежуточная конгруэнтно плавящаяся фаза постоянного состава в системе B-C. Состав: 50%A, 50%B.

6. М₁ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава в системе А–В. Состав: 40%А, 60%В.

7. М₂ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава в системе C-A. Состав: 90%C, 10%A.

8. М₃ – промежуточная инконгруэнтно плавящаяся фаза постоянного состава в системе C-A. Состав: 50%C, 50%A.

Растворимость компонентов друг в друге в твердом состоянии пренебрежительно мала, поэтому ее не учитываем. На стороны концентрационного треугольника наносим точки, отвечающие составам промежуточных фаз (S₁, M₁, M₂, M₃), перитектических (р₁, р₂, р₃) и эвтектических (е₁, е₂, е₃, е₄) нонвариантных точек в двойных системах.

По правилу фаз Гиббса трехфазные нонвариантные равновесия для двойных систем являются для тройных систем моновариантными (с = f–k +1 = =3–3+1 = 1) , поэтому из нонвариантных точек двойных систем (р₁, р₂, р_3, е₁, е₂, е₃, е₄) будут выходить моновариантные линии, отвечающие трехфазным равновесиям в тройной системе. Моновариантные линии будут пересекаться в точках, которые будут нонвариантными для тройной системы. Эти точки будут определять состав жидкой фазы, участвующей в четырехфазных нонвариантных равновесиях.

При вычерчивании проекции тройной системы необходимо помнить:

• четырехфазные реакции совместимы в одной трехфазной системе, если между ними имеется одно общее трехфазное равновесие с одинаковым набором фаз для двух соседних четырехфазных равновесий;

• если нонвариантное равновесие перитектическое, то к точке нонвариантного равновесия подходят 2 моновариантные линии, а выходит из нее одна, а если нонвариантное равновесие эвтектическое, то в точке нонвариантного равновесия сходятся 3 моновариантные линии;

• конгруэнтно плавящиеся фазы и твердые растворы на основе компонентов всегда находятся в области проекции ликвидуса этих фаз; инконгруэнтно плавящиеся фазы всегда лежат вне проекции ликвидуса этих фаз;

• центром кривизны моновариантных линий является более тугоплавкий компонент;

• четырехфазным перитектическим равновесиям на плоскости концентрационного треугольника отвечают четырехугольники, а эвтектическим равновесиям − треугольники, указывающие состав участвующих в равновесии фаз;

• метастабильные продолжения моновариантных линий ликвидуса должны проходить между двумя другими линиями ликвидуса фаз, участвующих в нонвариантном превращении.

Учитывая всё выше сказанное, был выбран вариант системы, в которой имеются следующие 5 четырёхфазных нонвариантных превращения:

Перитектические:

1. L_P1+A М₁+M₂, этому превращению отвечает четырехугольник P₁M₁AM₂;

2. L_P2+М₁ S₁+М₂, этому превращению отвечает четырехугольник P₂S₁М₁M₂;

3. L_P3+B S₁+M₁, этому превращению отвечает четырехугольник P₃S₁ BМ₁;

4. L_P4+M₂ S₁+M₃, этому превращению отвечает четырехугольник P₄S₁M₂M₃;

Эвтектическое:

L_E1→С+S₁+M₃, этому превращению отвечает треугольник CS₁M₃;

Диаграммы состояния граничных двойных систем А-В, В-С и А-С представлены на рис. 2,3,4 соответственно.

Составы промежуточных фаз и нонвариантных точек и температуры нонвариантных равновесий в системе А­­­–В–С представлены в таблице 1.

Проекция диаграммы состояния А-В-С на плоскость концентрационного треугольника представлена на рис. 5, рис. 6.

Проверка соответствия законам термодинамики положения нонвариантных точек на проекции в системе А-В-С: каждая перитектическая точка находится вне конодного треугольника, построенного на составах твёрдых фаз, а эвтектическая точка находится внутри конодного треугольника.

Таблица 1. Химический состав фаз, участвующих в реакциях.

Система, реакция	Химический состав фаз, %
	I				II				III				IV
	A	B	C	A		B	C	A		B	C	A		B	C
Система ABC
LP1+A М1+M2	54	23	23	100		0	0	40		60	0	90		0	10
LP2+М1 S1+М2	26	28	46	40		60	0	0		50	50	90		0	10
LP3+B S1+M1	18	45	37	0		100	0	0		50	50	40		60	0
LP4+M2 S1+M3	24	20	56	90		0	10	0		50	50	50		0	50
Cистема А-В	35	65	-	100		0	-	40		60	-	-		-	-
	27	73	-	0		100	-	40		60	-	-		-	-
Система В-С	-	60	40	-		100	0	-		50	50	-		-	-
	-	27	73	-		0	100	-		50	50	-		-	-
Система А-С	80	-	20	100		-	0	10		-	90	-		-	-
	40	-	60	10		-	90	50		-	50	-		-	-
	82	-	18	0		-	100	50		-	50	-		-	-

Примечание: цифры I-IV порядковый номер фазы.