
Геометрический синтез зубчатого механизма
По условию дано ∑Х=0,943мм, х1=0,489мм, αw=26° 48’27”,m=4, Z2/Z1=17/14.
Определяем основные размеры зубчатых колес и качественные характеристики зацепления.
Коэффициент суммы смещений
Х∑=х1+х2
Угол зацепления αw
inv αw=inv α+2((x1+x2)/z1+z2)tg α
где α=20º
Диаметры делительных окружностей
d1=mz1=56мм
d2=mz2=78мм
Диаметры основных окружностей
rв1=d1cosα/2=26,311мм
rв2=d2cosα/2=31,949мм
Делительное межосевое расстояние
a=(m(z1+z2))/2=62мм
Межосевое расстояние передачи со смещением
aw=a(cosα)/ cosαw=65,276мм
коэффициент воспринимаемого смещения
у=(аW-a)/m=0,8191мм
Коэффициент уравнительного смещения
∆у=х∑-у=0,12389396мм
Радиусы начальных окружностей
rw1=r1(cosα)/ cosαw=29,479мм
rw2=r2(cosα)/ cosαw=35,796мм
Контрольная проверка
aw=rw1+rw2=65,276мм – сошлось.
Радиусы вершин зубьев
ra1=m((z1/2)+ha*+x1-∆y)=33,808мм
ra2=m((z2/2)+ha*+x2-∆y)=38,972мм
Радиусы окружностей впадин зубьев
rf1=m((z1/2)-ha*+x1-с*)=25,304мм
rf2=m((z2/2)-ha*+x2-с*)=30,468мм
Высота зуба
h=ra1-rf1=8,504мм
Угол профиля точки по окружности вершин
αa1=arccos(rв1/ra1)=38,8993°
αa2=arccos(rв2/ra2)=34,9352°
Толщина зубьев по окружности вершин
Sa1=m(cosα/cosαw)[(π/2)+x1tgα-z1(invαa1-invα)=0,832мм
Sa2=m(cosα/cosαw)[(π/2)+x2tgα-z2(invαa2-invα)=1,888мм
Толщина зубьев по окружности вершин
должна быть больше или равна 0,4m,
коэффициенты высоты головки зуба
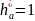 ,
коэффициент радиального зазора
,
коэффициент радиального зазора
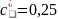 Коэффициент
торцового перекрытия
Коэффициент
торцового перекрытия
εα=(z1/2π)(tgαa1-tgα)+(z2/2π)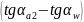 =1,86
=1,86
Допустимые значения коэффициента торцового перекрытия
εα≥1,2
полученое значение им удовлетворяет. Берем чертежную высоту зуба 30мм, находим K=0,2834 и вычерчиваем в масштабе зубчатое зацепление (приложение 5).
Заключение
В результате проделанной работы по решению задач был детально изучен графо-аналитический метод нахождения неизвестных величин, а так же рассмотрены скорости и ускорения с которыми движутся звенья компрессора, силы действующие на эти звенья и рассчитано и построено зубчатое зацепление.
