ФГБ ОУ ВПО

Московский государственный университет

путей сообщения (МИИТ)

Институт транспортной техники и систем управления

Кафедра «Машиноведение, проектирование, стандартизация и сертификация»

ДОМАШНЕЕ ЗАДАНИЕ

по дисциплине: «Теория механизмов и машин»

на тему

Использование общих методов проектирования и исследования механизмов для создания конкретных машин и приборов разнообразного назначения.

Выполнил: студент гр. ТПЛ-212

Торхов М.Ю.

Проверил: ассистент каф. МПСС

Андреев П.А.

Москва – 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………………………...……………3

ПОСТРОЕНИЕ ПЛАНА МЕХАНИЗМА………………………………..……...…………..4

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ЗВЕНЬЕВ МЕХАНИЗМА

С ПОМОЩЬЮ ПЛАНА СКОРОСТЕЙ…………………………………………………….5

ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ……………………………………………………7

КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ МЕХАНИЗМА……………………………………10

ГЕОМЕТРИЧЕСКИЙ СИНТЕЗ ЗУБЧАТОГО МЕХАНИЗМА……………………..…15

ЗАКЛЮЧЕНИЕ………………………………………………………………………………..17

ПРИЛОЖЕНИЯ………………………………………………………………………...……..18

ВВЕДЕНИЕ

Целью данной работы является изучение графо-аналитического метода для нахождения неизвестных величин, при решении векторных уравнений, в частности рассмотреть скорости, ускорения и действующие силы на звенья кривошипно-шатунного механизма, а так же детально разобрать принцип зубчатого зацепления, на примере компрессора. Компрессоры подвижного состава железных дорог Российской Федерации одноцилиндровые и многоцилиндровые состоят из кривошипа (коленчатого вала) и присоединенных к нему структурных групп (группы Ассура). Данный компрессор имеет V-образное расположение цилиндров

Построение плана механизма

Данный механизм состоит из кривошипа 1,шатунов 2 и 4, ползунов (поршней) 3 и 5. С точки зрения структуры этого механизма он состоит из механизма 1го класса 1го порядка (звено 1) двух структурных групп 1го класса 2го порядка 2 модификации (см. приложение 1).

Кинематический расчет механизма компрессора сводится к расчету параметров движения звеньев, входящих в состав указанных групп. При этом алгоритм определения этих параметров будет одним и тем же для каждой группы независимо от положения звеньев в механизме.

Для кинематического расчета механизма задается его кинематическая схема с указанием размеров звеньев, положение кривошипа в рассматриваемый момент времени и скорость его вращения.

План механизма (кинематическая схема) для выполнения расчетов графоаналитическим методом строится с использованием масштаба.

При расчете механизмов часто применяют так называемый масштабный коэффициент К_ℓ, равный отношению действительных размеров звеньев к их размерам на чертеже, т.е. l_ОА=0,04м – по условию, возьмем на чертеже этот отрезок 25мм. Тогда

Т.е. в 1мм чертежа содержится 1,6мм действительного размера механизма.

Далее определяем недостающие размеры звеньев. Задано λ=ℓ_OA/ℓ_AB=1/3,8. Отсюда l₂=0,04*3,8=0,152м, и l₂=95мм в масштабе. Аналогично из заданного отношения AS₂/AB=0,4 находим AS₂=0,0608м и AS₂=38мм. Так как шатуны одинаковы то l₂=l₄, AS₂=АS₄.

Для выбора заданного положения кривошипа траектория точки А (окружность)разбивается на 12 равных частей от начала отсчета, в качестве которого принимается положение точки А на линии ОВ. Ставим точку А в соответствии с заданием в 6 положение.

Положение точек В и С на линии ОВ и ОС находим методом «засечек» циркулем, установленным в точку А и содержащим размер звеньев АВ и СD, в принятом масштабе. На звеньях АВ и AС необходимо указать положение их центров масс, отмеряя от точки А размеры AS₂ и АS₄ в масштабе соответственно.

Определение скоростей звеньев механизма с помощью плана скоростей

Данный кривошип вращается с постоянной угловой скоростью, которая определяется исходя из известного числа оборотов n₁=800 мин^-1 по формуле

Вектор скорости точки, движущейся по какой-либо траектории всегда направлен по касательной к траектории в этой точке. В нашем случае вектор скорости в точке А направлен по касательной к окружности в точке А, т.е. перпендикулярен к радиусу ОА.

Линейная скорость точки А тогда равна

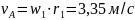
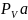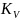Из произвольной точки P_V на плоскости проводим отрезок длины 100мм, перпендикулярно АО, который будет в масштабе (масштабный коэффициент скорости) изображать скорость точки (см. приложение 1). Величина будет равна:

т.е. масштабный коэффициент показывает сколько единиц скорости содержится в одном миллиметре отрезка .

В сложном движении скорость точки В определим в соответствии с векторным уравнением:

(1)

В векторном уравнении (1) скорость точки А известна по величине и по направлению, скорости V_B и V_A известны только по направлению. Скорость точки В направлена по линии ОВ(движение ползуна-поршня 3 по направляющим), вектор скорости точки В относительно точки А будет направлен перпендикулярно отрезку АВ как радиусу окружности, описываемой точкой В в ее относительном движении вокруг точки А. В соответствии с этим из точки P_V проводим луч, параллельный линии ОВ, а из точки а отрезка P_Va луч, перпендикулярный АВ. Пересечение этих лучей в точке b определяет отрезок P_Vb, который в принятом масштабе изображает скорость точки В, а отрезок ab изображает скорость точки В относительно точки А.

Направление векторов этих скоростей должно соответствовать уравнению (4), а их величина определяется из соотношений:

V_B=K_VP_Vb, м/с

V_BA=K_Vab, м/с

В нашем случае V_BA=3,25 м/с, V_B=1,1 м/с

Аналогичным образом определяются скорость точки С и точки С относительно точки А.(V_C=3,02 м/с ; V_CA=0,9 м/с) Положение точек S₂ и S₄( центров масс), звеньев на плане скоростей определяется в соответствии с условием подобия : их расположение на плане скоростей подобно расположению на схеме механизма. Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из соотношения:

V_S2=K_VP_Vs₂, м/с

V_S4=K_VP_vs₄, м/с

V_S2=2,18 м/с; VS4=3,22 м/с

Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении.

Как уже говорилось, отрезок плана скоростей аb (вектор) обозначает скорость точки В относительно точки А. Разделив величину скорости 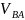на действительную длину звена АВ получим угловую скорость звена 2, т.е.

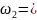
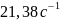
Для определения направления угловой скорости ω₂ необходимо вектор скорости приложить к точке В.

Угловую скорость звена 4 и ее направление определим аналогичным образом :