29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)

Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейтеміз.

Кез келген γ Є IR, A берілсін. A= { a_ij }

γА= { γa_ij }

Қасиеттері:

1. 1·A=A

2. (γ·μ)·A= γ·(μ·A)=μ·(γ·A)

3. γ·(A+B)=γ·A+γ·B

4. (γ+μ)·A=γ·A+μ·B

30. Матрицаларды қосу амалы және оның қасиеттері (дәлелдеуімен). Матрица дегеніміз сандардан тұратын таблица. Матрицалар квадрат, үшбұрышты т.с.с. болады. Матрицаларды қосу оның элементтері (сәйкес) бойынша жүргізіледі. Транспонирленген матрица. А=

α_ίJ– сандары матрицаның элементтері. i –жол, j –баған. Қысқаша А=( α_ίJ). Егер барлық α_ίJ = 0 болса, онда матрица нөлдік матрица. Егер екі А және В матр-ның сәйкес орындарда тұратын элементтері тең болса, онда А=В. Егер жол мен бағанныңгер жол мен бағанның орындарын ауыстырсақ, онда транспонирленген матрица аламыз. Реттері бірдей матрицаларды қосуға болады. Айталық, А=( α_ίJ), В=( b_ίJ) болсын, сонда А+В = (α_ίJ + b_ίJ). Матрицаларды қосудың қасиеттері:

1. А+В = В+А; 2. А+0 = А ; 3. А+(В+С) = (А+В)+С. Егер А матрицасының барлық элементтерін µ санына көбейтсек, онда µ А = (µ α_ίJ). Матр-ны санға көбейтудің қасиеттері: 1)1*А=А*1=А ; 2) µ (ℓ А) = (µ ℓ )А ; 3) µ (А+В) = µА+ µВ; 4) (µ+ℓ)А = µ А + ℓ А;

Дәләлдеуі: А =

В = А+В = .

31. Матрицаны аудару амалы және оның қасиеттері. Матрицаның жолдарымен бағандарының орындарын ауыстыруды оны транспонирлеу деп аталады. А матрицасына осы амалды қолданғанда шыққан матрицаны А' арқылы белгілейміз. А=

А'=

A^/ - n*m; A – m*n;

Аудару амалының қасиеттері:1)(A^/)^/ =A ;               2) (λA)^/ = λ* A^/ ;  

 3) (A+B)^/ = A^/+B^/; 4) (A*B)^/ = B^/*A^/. Дәлелдеуі: А = А'=

32.  Матрицаларды көбейту A-m*k  ретті,   B-k*n  ретті.

C_ij=α_i1+b_1j+ α_i2+b_2j+….+ (i=1,2……..m) (j=1,2……...n)

формулаларымен анықталатын C=A·B матрицасы А мен В матрицасының көбейтіндісі деп аталады.С матрицасы ретті m* n болады.

Матрицаға қолданылатын амалдар қасиеттері:

1)A+B=A+B;

 2) (A+B)+C=A+(B+C);    3)λ*(A+B)= λ*A+ λ*B ;    4) A*(B+C)=A*B+A*C;

5) (A+B)*C=AC+BC ;          

6) λ(A*B)=(λ*A)*B=А*( λ*B); 7) A*(B*C)=(A*B)*C. Дәләлдеуі:  A = 2 х 3 ретті,  B =   3 х 3 ретті

A*B = .

33. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.

А=(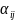 ) (P) қандай да бір мат/а бол/н.

А мат/ң жол/на элементар түрлендірулер жасап сатылыSмат/н алу керек д.е.Егер А мат/сы нөл/к мат/а болса,онда S=А=0. Егер А≠0 болса,она келесі процедура/ды біртіндеп жасаймыз.

1.A мат\ң кем дегенде бір нөлдік емес бағаны бар. Нөлдік емес баған/ң ең кіші нөмірін деп белгілейік. ші бағанындағы нөлден өзге элементінің біреуін ,айталық элементін ерекше белгілеп алып оны бастаушы элемент деп атаймыз.

2.(a)түрлендірудің көмегімен астаушы элементі орналасқан ші жолын 1-ші жолмен алмастырып В мат/н аламыз.

B=

Бұл жерде .

3.B мат/ң 2-ші жолынан 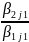коэф/ке көбейтілген 1-ші жолын, 3-ші жолынан

коэф/ке көбейтілген 1-ші жолын, т.с.сk- ші жолынан коэф/ке көбейтілген 1-ші жолды алып тастасақ,

C=

мат/н аламыз. Бұл жерде , егер j= ,n болса : , егер i=2,k, j= болса.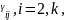 j= элементтерінен құралған мат/ны арқылы белгілейік. Егер D=0 болса онда S=C, керісінше D мат/на жоғарыда келтірілген процедураларын қайталаймыз, яғни С мат/ң 1-ші жолымен 1- ші бағандары алгоритмімізде одан әрі өзгермейді.

Гаусс алгоритмін бағандарға да жургізуге болады.

34. Векторлар жүйесіне қолданылатын элементар түрлендірулер. P-қандайда бір өріс, n-кез келген натурал сан ,ал болсын. векторлар жүйесіне жасалатын элементар түрлендірулер 3 типке бөінеді:

1. жүйенің кез келген екі век/ң орнын алмастыру;

2. жүйенің қандайда бір век/н P өрісінің кез келген нөлден өзгеше коэф/не көбйту;

3. жүйенің қандайда бір век/на басқа век/н кез келген P-ға тиісті коэф/ке көбейтіп алып,содан кейін қосу.

(P) мат/ң жол/н арифметикалық кеңістігінің,ал арифметикалық кеңістігінің век/р жүйелері ретінде қарастыруға болады.Ендеше мат/ң жолдарына не бағандарына элементар түрлендірулерді жасауға болады.