
- •Векторлар . Векторларды қосу амалы және оның қасиеттері (дәлелдеуімен)
- •2. Векторларды санға көбейту амалы және оның қасиеттері (дәлелдеуімен)
- •3. Сызықтық тәуелді векторлар жүйесі. Сызықтық тәуелді векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •4. Сызықтық тәуелсіз векторлар жүйесі. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •6. Компланар векторлардың анықтамасы. Үш вектордың компланар болу белгісі. (дәлелдеумен)
- •8. Вектордың векторлық проекциясы және оның қаситеттері.
- •9. Екі вектордың скаляр көбейтіндісі және оның қасиеттері
- •10. Скаляр көбейтіндіні тікбұрышты координаталар жүйесінде есептеу формулалары.
- •12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
- •13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.
- •Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
- •15. Жазықтықтағы түзудің нормал теңдеуін қорытып шығару.
- •17. Жазықтықтың теңдеулерілерін қорытып шығару.
- •19. Екі жазықтықтың өзара орналасуы. (дәлелдеумен)
- •20. Екі жазықтықтың арасындағы бұрыш.
- •21.Жазықтықтың нормаль векторы. Жазықтықтың нормал теңдеуін қорытып шығару. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық.
- •22. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың формуласын қорытып шығару.
- •24. Кеңістіктегі түзумен жазықтықтың өзара орналасуын зерттеу.
- •25. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыш.
- •26. Эллипс. Канондық теңдеу
- •29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)
- •33. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.
- •35. Векторлар жүйесінің базасы және рангі.
24. Кеңістіктегі түзумен жазықтықтың өзара орналасуын зерттеу.
Р:
 =
= =
= ;
;
 =(l,m,n)
– бағыттаушы вектор; (.)
=(l,m,n)
– бағыттаушы вектор; (.) (
( ;
; ;
; )
) P;
P;
π: Ax+By+Cz+D=0;
1) P түзуі π жазықтығымен беттеседі ↔ (.) є π, //π ↔
A
+B
+C
+D=0,
Al+Bm+Cn=0;
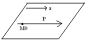
2 )
P∩π=Ø(бос
жиын);
(.)
єπ,
//π
← A
+B
+C
+D≠0,
Al+Bm+Cn=0;
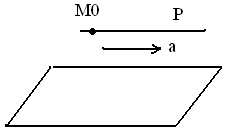
)
P∩π=Ø(бос
жиын);
(.)
єπ,
//π
← A
+B
+C
+D≠0,
Al+Bm+Cn=0;
 ҮҮ
Ђ
ҮҮ
Ђ
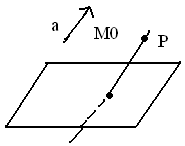
3)
P∩π = жалғыз
нүктеде ↔
//
π ↔ Al+Bm+Cn≠0;
25. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыш.
Кеңістіктегі
L түзуі мен Q жазықтығының арасындағы
бұрыш деп, берілген L түзуі мен оның
жазықтығы проекциясыының арасындағы
сыбайлас екі бұрыштың бірі
 бұрышын айтады.
бұрышын айтады.
L
түзуі мен
 =
= канондық теңдеуімен берілсін.
бұрышын түзудің бағыттаушы
канондық теңдеуімен берілсін.
бұрышын түзудің бағыттаушы
 және жазықтықтың нормаль
және жазықтықтың нормаль
 векторының арасындағы
векторының арасындағы
 бұрышы арқылы өрнектейтін болсақ:
бұрышы арқылы өрнектейтін болсақ:
:
= ;
ал
;
ал
 =
=
Бірақ
барлық кезде
 деп қарастыратын болады. Өйткені сыбайлас
бұрыштардың синустары өзара тең:
деп қарастыратын болады. Өйткені сыбайлас
бұрыштардың синустары өзара тең:
Ендеше
 деп
алуға болады.
деп
алуға болады.
 =|
=| =
= .
ЕгерL || Q болса, онда
.
ЕгерL || Q болса, онда

Am+Bn+Cp=0.
Егер Л перпендикуляр Й болса,
 Онда бағыттаушы
және жазықтықтың нормаль
векторы өзара коллинеар болады.
Онда бағыттаушы
және жазықтықтың нормаль
векторы өзара коллинеар болады.

26. Эллипс. Канондық теңдеу
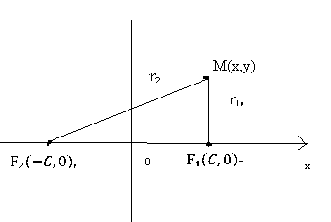
Анықтама
 және
және
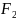 дейін арақашықтарының қосындысы
константа (өзгермейтін сан) болатын
жазықтықтың нүктелер жиыны эллипс
дейін арақашықтарының қосындысы
константа (өзгермейтін сан) болатын
жазықтықтың нүктелер жиыны эллипс
 деп аталады.
деп аталады.
 -
эллипстың фокустары.
-
эллипстың фокустары.
 -фокалдық
радиустар.
-фокалдық
радиустар.
Егер
кез келген (.)M(x,y) үшін

Енді
 -
қарастырайық.
(.)M(x,y)
-
қарастырайық.
(.)M(x,y) -
кез келген нүктесі.
-
кез келген нүктесі.
Онда


Бізде
.
Сонда



Бізде
 деп
белгілейік.
деп
белгілейік.
 элипстің
канондық теңдеуі
элипстің
канондық теңдеуі
Фокалдық радиустарды есептеу
= =
=
Бізде,
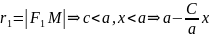 >0
>0
Эллипстің эксцентриситеті.
 e-
эксцентриситет
e-
эксцентриситет
Бізде

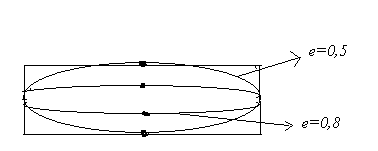
Егер
 ,онда
эллипс фокалдық өсіне қарай жиналады.
,онда
эллипс фокалдық өсіне қарай жиналады.
Егер
 ,онда
эллипс шеңберге жуықтайды.
,онда
эллипс шеңберге жуықтайды.
Эллипстің параметрлік теңдеуі.
Мына
теңдеуді қарастырайық:

Енді
 болсын.
болсын.
Онда


Сондықтан, эллипстің параметрлік теңдеуі:
27. Гипербола (канондық теңдеуін қорыту, фокалдық радиустар, эксцентриситет, параметрлік теңдеу, асимптоталар). F1,F2 нүктелеріне дейінгі арақашықтықтарының айырмасының модулы тұрақты сан болатын жазықтықтағы нүктелер жиынын гипербола деп атаймыз.
|r1-r2|=2a
Фокалдық радиустар:
r1=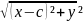 ,
r2=
,
r2=
Канондық теңдеуін қорыту:
| –
|=2a
–
|=2a
= ±2a
±2a
(x-c)2+y2=(x+c)2+y2± ²+4a2
²+4a2
x2-2cx+c2y2=x2+2cx+c2+y2±4a +4a2
cx+a2=±a
c2x2+2a2cx+a4=a2x2+2a2cx+a2c2+a2y2
x2(c2-a2)-a2y2=a2c2-a4
x2(c2-a2)-a2y2=a2(c2-a2)
c2-a2=b2
x2b2-a2y2=a2b2
 -
-
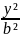 = 1
= 1
Гиперболаның экцентриситеті деп, келесі санды айтамыз:
 c>a,
e>1
c>a,
e>1
Гиперболалық косинус пен гиперболалық синус:
cht=
sht
=

Параметрлік теңдеу:
cht
=
 , sht=
, sht=

Асимптота дегеніміз гипербола шексіз жуықтайтын түзу.
y
=
 x;
y= -
x.
x;
y= -
x.
28.
Парабола.
Бізге жазықтықта (.) F нүктесі және
 түзуі берілсін,
түзуі берілсін,
 F
F түзуіне тиісті емес.
түзуіне тиісті емес.
Анықтама.Жазықтықтағы
нүктелер жиынын парабола деп атайды,
егер сол жиынның әр бір нүктесінің
 нүктесіне дейінгі арақашықтығы және
түзуіне дейінгі арақашықтықтары тең
болса.
нүктесіне дейінгі арақашықтығы және
түзуіне дейінгі арақашықтықтары тең
болса.

 y M
y M
d r

D( ,,0)
,,0) 
 x
x
Бұл
жерде F – фокус,
директриса, фокуспен директрисаның
арасындағы арақашықты параболаның
параметрі
 деп
атайды.
деп
атайды.
Параболаның
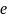 – сін
бірге тең деп аламыз,
– сін
бірге тең деп аламыз,
 .
.
Бізде
 ,
,
 егер
егер онда
минус таңбасы шығады
онда
минус таңбасы шығады



Сондықтан,
1)
егер
(.)
 парабола
парабола

2)
егер
(.) парабола
парабола

Параболаның түрін зерттеу.
Бізде
 - тің дәрежесі жұп сан, сондықтан
- тің дәрежесі жұп сан, сондықтан
 осі
осі
 параболаның симметрия осі. Параболаның
симметия осімен қиылысу нүктесін
параболаның төбесі деп атайды.
параболаның симметрия осі. Параболаның
симметия осімен қиылысу нүктесін
параболаның төбесі деп атайды.
 – нүктесі (1) – дің төбесі.
– нүктесі (1) – дің төбесі.
Бізде
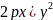 ,
,

 теңдеуін
шешейік.
теңдеуін
шешейік.
 ,
бұл жерде
,
бұл жерде
 қарастырайық. Сонда
жарты
интервалда
қарастырайық. Сонда
жарты
интервалда
 өспелі
функция және
өспелі
функция және

Сол
сияқты
 жағдайды
қарастыруға болады.
жағдайды
қарастыруға болады.
