
- •Векторлар . Векторларды қосу амалы және оның қасиеттері (дәлелдеуімен)
- •2. Векторларды санға көбейту амалы және оның қасиеттері (дәлелдеуімен)
- •3. Сызықтық тәуелді векторлар жүйесі. Сызықтық тәуелді векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •4. Сызықтық тәуелсіз векторлар жүйесі. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •6. Компланар векторлардың анықтамасы. Үш вектордың компланар болу белгісі. (дәлелдеумен)
- •8. Вектордың векторлық проекциясы және оның қаситеттері.
- •9. Екі вектордың скаляр көбейтіндісі және оның қасиеттері
- •10. Скаляр көбейтіндіні тікбұрышты координаталар жүйесінде есептеу формулалары.
- •12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
- •13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.
- •Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
- •15. Жазықтықтағы түзудің нормал теңдеуін қорытып шығару.
- •17. Жазықтықтың теңдеулерілерін қорытып шығару.
- •19. Екі жазықтықтың өзара орналасуы. (дәлелдеумен)
- •20. Екі жазықтықтың арасындағы бұрыш.
- •21.Жазықтықтың нормаль векторы. Жазықтықтың нормал теңдеуін қорытып шығару. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық.
- •22. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың формуласын қорытып шығару.
- •24. Кеңістіктегі түзумен жазықтықтың өзара орналасуын зерттеу.
- •25. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыш.
- •26. Эллипс. Канондық теңдеу
- •29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)
- •33. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.
- •35. Векторлар жүйесінің базасы және рангі.
17. Жазықтықтың теңдеулерілерін қорытып шығару.
П-жазықтық,
 -тіркелген
нүкте. (
-тіркелген
нүкте. ( ,
,
 -кез
келген
нүкте. (
-кез
келген
нүкте. ( ,
,

 =
= ,
(
,
( )
M
)
M компланар
компланар
 (1)
векторлық түрдегі параметрлік теңдеуі
(1)
векторлық түрдегі параметрлік теңдеуі

x
=
 => y =
=> y =
 координаталық түрдегі параметрлік
теңдеуі
координаталық түрдегі параметрлік
теңдеуі
Z
=

x
-
 => y -
=> y -

Z
-

 =>
=0
(3) бір нүкте арқылы өтетін және екі
векторға параллель жазықтыктың теңдеуі
=>
=0
(3) бір нүкте арқылы өтетін және екі
векторға параллель жазықтыктың теңдеуі
19. Екі жазықтықтың өзара орналасуы. (дәлелдеумен)
1-теорема.

 және
және
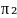 жазықтықтары беттеседі сжтсғ,егер
олардың теңдеуіндегі барлық коэффициенттер
өзара тең болса.
жазықтықтары беттеседі сжтсғ,егер
олардың теңдеуіндегі барлық коэффициенттер
өзара тең болса.
 ↔
↔
 =
= =
=
 =1
=1
 жаз-ы
параллель болады сжтсғ,егер теңдеудегі
x,y,z алдындағы коэффициенттері пропорционал
болса,ал бос мүшесі пропорционал
болмаса.
жаз-ы
параллель болады сжтсғ,егер теңдеудегі
x,y,z алдындағы коэффициенттері пропорционал
болса,ал бос мүшесі пропорционал
болмаса.
 =
=

 =2
=2
 =1
=1
жаз-ы түзу қиылысады сжтсғ,егер мына шарт орындалса,яғни матрица рангі 2-ге тең болса.
 =2
=2
1-теорема.
Дәлелдеу. ,
=
,
= ,
,
 =
=
,
=
 ,
=
,
= -
- +
+

 -
- =0
,
=0
,

Егер
екі жазықтық жалпы түрдегі теңдеулерімен
А1х+В1у+С1z+D1=0
A2x+B2y+C2z+D2=0
берілген болса, онда олардың арасындағы
бұрыш үшін олардың нормаль векторларының
арасындағы бұрыштың айтамыз.Өйткені
екі жақты бұрыштың сызықтық бұрышпен
өлшенетіні белгілі.Ал екі нормал
арасындағы бұрыш осы сызықтық бұрыш
болып саналады.Жазықтықтардың
теңдеулерінен олардың нормаль векторларын
N1=A1i+B1J+C1k,
N2=A2i+B2j+C2k табамыз,ал проекциялары
арқылы берілген ве кторлардың арасындағы
бұрыштың косинусының формуласы
Cosф=(N1+N2)
/ |N1|*|N2|=A
1A2+B
1B2+C
1C2
/
20. Екі жазықтықтың арасындағы бұрыш.
 *
*
 Сонымен
екі жазықтық арасындағы бұрышты осы
формула арқылы табуға болады.
Сонымен
екі жазықтық арасындағы бұрышты осы
формула арқылы табуға болады.
21.Жазықтықтың нормаль векторы. Жазықтықтың нормал теңдеуін қорытып шығару. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық.
Бізге Ах+Ву+Сz+D=0 түрінде жазықтық берілсін. Осы жазықтықтың нормаль векторы деп осы жазықтыққа перпендикуляр N(A;B;C) түрінде болатын векторды айтамыз. Жазықтықтардың нормаль векторы N коорд.осьтерімен сәйкес α,β,γ бұрыштарын жасайтын болса, онда оны N=(cosα)*i+(cosβ)*j+(cosγ)*k түрінде жазуға болады.
=>cos(x-x0)+cos(y-y0)+cos(z-z0)=0 н/е
cosα*x+cosβ*y+cosγ*z-(x0*cosα+y0*cosβ+z0*cosγ)=0 түрінде жазуға болады.
X*cosα+y*cosβ+z*cosγ-p=0 |
-жазықтықтың нормаль теңдеуі. Ал жалпы теңд.түрде берілсе Ах+Ву+Сz+D=0/* μ
μ * Ах+ μ *Ву+ μ *Сz+ μ *D =0 μ * А= cosα, μ *В= cosβ , μ *С= cosγ cos2α+cos2β+cos2γ=1
cos2α+cos2β+cos2γ=1
|
μ
2*(A2+B2+C2)=
cos2α+cos2β+cos2γ=1
μ=± - нормалаушы көбейткіш.
- нормалаушы көбейткіш.
22. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың формуласын қорытып шығару.
Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық.
Кеңістікте бір М0 (x0, y0, z0) нүктесі және Ах+Ву+С z+D=0. Жалпы теңдеуі мен Q жазықтығы берілген. Олардың арасындағы қашықтықты d деп белгілеп, яғни М0 нүктесінен Q жазықтығына түсірілген перпендикуляр ұзындығын мына формула
d= арқылы
табуға болады.
арқылы
табуға болады.

Q –нүктесінен π жазықтығына перпендикул түсірейік.
(.)
Q(
 ,
(.)
,
(.)
| = d((.)
= d((.)
 (
(
 ,
, |
| (
^
(
^ =±d;
=±d;
(
, -(
-( -p=0=
-p=0=
d=| |
|
d
=


23.
Кеңістіктегі екі түзудің өзара
орналасуын зерттеу. Кеңістікте
ОХУZ тік бұрышты Декарт координаталар
жүйесі берілсін Алдымен L1
мен
L2
екі түзуінің өзара орналасуын қарастырайық.
Бұл түзулер
 L1,
L1,
 L2
берілген нүктелер және берілген а1//
L1,
а2//
L2
бағыттаушы векторлармен толық анықталады.
Ендеше олардың параллел болуы, бір
нүктеде қиылысуы, беттесуі, айқасуы
берілген нүктелер және векторлар арқылы
сипатталуы керек.
L1
мен
L2
түзуінің канондық түзуі берілсін.
L2
берілген нүктелер және берілген а1//
L1,
а2//
L2
бағыттаушы векторлармен толық анықталады.
Ендеше олардың параллел болуы, бір
нүктеде қиылысуы, беттесуі, айқасуы
берілген нүктелер және векторлар арқылы
сипатталуы керек.
L1
мен
L2
түзуінің канондық түзуі берілсін.
L1: =
= =
= ,
L2:
,
L2:
 =
= =
=
Енді
бағытталған кесінділердің коллинеарлық
шарты мен аралас көбейтіндіні есептеу
формуланы қолдансақ, жоғары L1
мен
L2-нің
өзара орналасу шарттары келесі түрде
жазылады: L1
//
L2

 =
=
 - параллель (1)
- параллель (1)
| =1
- бір нүктеде қиылысады.
=1
- бір нүктеде қиылысады.  =0 және
=0 және

 (2)
(2)
L1
мен L2
айқасады
 (3)
(3)
L1
мен L2
беттеседі
(x2-x1)
:
(y2-y1)
: (z2-z1)=
 (4).
(4).
