Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
1-теорема.
P₁:A₁x+B₁y+C=0
p₂:A₂x+B₂y+C=0
1) P₁ мен p₂ түзулері беттеседі сжтсғ,егер де олардың теңдеулеріндегі барлық коэффиценттер пропоционал болса.
1)
P₁
p₂
=
,
2)мен түзулерінің қиылысуы бос жиын болады, сжтсғ, егер олардың теңдеулеріндегі х пен у-тің алдындағы коэфф, пропоционал болып, үшінші коэф-і пропоционал болмаса
2)
P₁
p₂
=
,
3)мен түзулері жалғыз нүктеде қиылысады, сжтсғ, егер олрадың теңдеулеріндегі х пен у-тің алдындағы коэф-і пропоционал емес болса
3)
P₁
p₂=(.)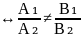
Формулалар(және жазықтықтағы екі түзудің арасындағы бұрыш)
p₁: x=x₁+l₁t
y=y₁+m₁t
,
=(l₁m₁)
p₂: x=x₂+l₂t
y=y₂+m₂t
,
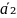=(l₂m₂)
tg(p₁^p₂)=tg(
^
)=
2) P₁:A₁x+B₁y+C=0 , =(-B₁,A₁)
p₂:A₂x+B₂y+C=0 , =(-B₂,A₂)
tg(p₁^p₂)=
3)p₁:y=k₁x+b₁ , =(1,k₁)
p₂:y=k₂x+b₂, =(1, k₂)
tg
(p₁^p₂)=
Ескерту! 1) p₁⏊p₂↔l₁l₂+m₁m₂=0
A₁A₂+B₁B₂=0
1+k₁*k₂=0,
k₂=-
-
2)p₁
p₂↔
=
,
=
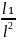, k₂=k₁
15. Жазықтықтағы түзудің нормал теңдеуін қорытып шығару.
D түзуі өзінің жалпы теңдеуі арқылы берілсін.
Ax+by+c=0, + /1/
=
(A,B)⏊d болатыны бізге белгілі. Енді мына
дербес жағдайды қарастырамыз.
=
=(cos
Яғни,n-векторын бірлік вектор деп санайық. Бұл жағдайда бірлік вектордың координаталары сәйкес бағыттаушы косинустар болады. Сонда түзу теңдеуі былай жазылады:
xcos
\2\
Мұнда
p
0деп
санауға болады,себебі егер олай
болмаса,онда n векторының орнына -
векторын қарастырамыз.
/2/-теңдеуді
түзудің нормаланған теңдеуі деп атаймыз.
Бұдан,егер
+
=1,c
Болса,онда
/1/теңдеу нормаланған теңдеу болып
шығады. /2/-теңдеуді векторлық түрде
былай жазамыз:
-p=0
\4\
Мұндағы
=
айнымалы M(x,y) нүктесінің радиус-векторы.
Нормаланғанбаған
/1/-теңдеуді /2/-формуланы пайдаланып,нормаланған
түрге оңай келтіріп алуға болады. Ол
үшін /1/-теңдеудің екі жағында кейінірек
анықталатын
көбейткішіне көбейтіп,одан шыққан мына
теңдеуді
\6\
Нормаланған
теңдеу деп санаймыз. Олай болса
/3/-формуланың негізінде
+
=1
және
\7\
Бұдан
-ның бізге керек болып отырған мәнін
табамыз,яғни
=
\8\
Бұл
сан /1/-теңдеуді нормалайтын көбейткіш
деп аталады. /2/-теідеудегі p
болғандықтан,егер с
0
болса,онда
көбейткішінің
таңбасы С коэффицентінің таңбасына
қарама-қарсы болып алынады. Ал,егер с=0
болса,онда /8/-формуладағы
таңбасы ретінде кез-келген таңбаны
алуға болады. /6/ және /8/-формулаларынын
мына теңдеуді аламыз
=0
Бұл жалпы теңдеуі арқылы берілген түзудің нормаланған теңдеуі болып табылады
16.Жазықтықтағы
нүктеден түзуге дейінгі арақашықтық.
Жазықтықтағы түзудің координаталық
осьтерге қатысты орналасуының дербес
жағдайлары. М(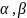
)
нүктесінен Ах+Ву+С=0 теңдеуімен берілген
L түзуіне дейінгі арақашықтық
(M,L)=
формуласымен есептеледі.Дәлелдеу
(M,L)=
теңдігі мен
=0
формуласынан және
=
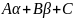формулалардан бірден көрініп тұр.Теорема:
Егер (
)
сандар жұбы М нүктесінің Декарт
кординаталары, ал
=0
теңдеуі L түзуінің нормаланған теңдеуі
болса, онда
=
.
Бұл теорема көп жағдайларда пайдалануға
ыңғайлы.