13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.

Мына есепті шығарайық:бағыттаушы векторы =(l,m)–ке тең,берілгенM˳(x˳,y˳) нүктесін басып өтетін d түзуінің теңдеуін табыңдар.M(x,y) d нүкте болсын,сонда =(x-x˳,y-y˳). Cондықтан || /1/,бұдан = - (канондық теңдеу), яғни кез-келген нүктесінің M(x,y) координаталары /1/- теңдеуді қанағаттандырады.

Керісінше ,M*(x*,y*) нүктесі,координаталары \1\ теңдеуді қанағаттандыратын нүкте болсын,яғни = . Олай болса, 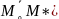=(x*-x˳,y*-y˳) және =(l,m) векторлары коллинеар болады,демек M*(x*,y*) . Сөйтіп /1/ -теңдеу іздеген теңдеуіміз болып шықты. Бұл теңдеу түзудің канондық теңдеуі деп аталады. /2/-формуладағы бөлшектердің біреуінің бөлімі нөлге айналуы мүмкін. /әрине 0 болғандықтан екі бөлшектердің бөлімдері бір уақытта нөлге тең болмайды. Бұл жағдайда, пропорциясын ad=bc теңдігінің орындалуын пара-пар деп түсінгендіктен,ол бөлшектің сәйкес алымын нөлге тнң деп санаймыз.

/1/теңдеудегі теңдіктің оң және сол жағындағы бқлшектердің жалпы мәнін t деп белгілейік. Сонда t парметрінің өзгеру облысының барлық сан осі (R) болатынына көз жеткізу қиын емес.

Шынында да,бөлшектердің кемінде біреуіңің бөлімі нөлге тең емес,демек,бөлшектің сәйкес алымы кез-келген мәнді хабарлай алады. Олай болса t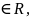 яғни - Сонымен /1/-теңдеуден немесе теңдеулерін аламыз.

x-x˳=lt , y-y˳=mt немесе \2\

/2/-теңдеулер түзудің парметрлік теңдеулері деп аталады.

Анықтама(Жазықтықтағы түзудің жалпы теңдеуі.).Ax+By+C=0 \1\ теңдеу түзудің жалпы теңдеуі деп аталады.

1-теорема.Жалпы теңдеуі арқылы анықталған түзуі,сол түзудің нормалдық векторы деп аталатын n=(A,B) векторына перпендикуляр болады.\1\ теңдеу кем дегенде бір (x˳,y˳) шешімі бар болатынын тексеру қиын емес.Шынында да,A және B коэффициенттері бір уақытта нөлге айналмайтын болғандықтан,A≠0 деп алайық.Егер y=y˳ десек,онда \1\ теңдеуден мына мәнді шығарамыз: x˳=-(B/A)y˳-(C/A).Демек,Ax˳+By˳+C=0 \2\

теңбе-теңдігі орындалатындай M˳(x˳y˳) нүктесі табылады.Егер \1\ теңдеуден \2\ теңбе-теңдігін мүшелеп алып тастасақ,онда \1\ теңдеуге мәндес мына теңдеуді аламыз:A(x-x˳)+B(y-y˳)=0 \3\.

\3\ шарт d түзуінде жатқан кез келген M˳M=(x-x˳,y-y˳)векторы мен n=(A,B) векторының перпендикулярлық (ортоганалдық) шартын (белгісін) көрсетеді.

2-анықтама./3/-теңдеу M˳(x˳,y˳) нүктесі арқылы өтетін. =(a,b) векторына перпендикуляр түзу теңдеуі деп аталады.

2-теорема. Нөлдік емес =(l,m) векторы /1/-жалпы теңдеумен берілген d түзуінің бағыттаушы векторы үшін Al+bm=0 \4\ шартының орындалуы қажетті және жеткілікті.

Қажеттілік. =(l,m) 0 векторы

Ax+by+c=0, +

tеңдеуімен анықталған d түзуінің бағыттаушы векторы дейік. 1-теорема негізінде =(A,B) болады. Бұдан. демек,бұл екі вектордың скалярлық көбейтіндісі нөлге тең,яғни * =A*l+ B*m=0. Қысқаша: s векторы d түзуінің бағыттаушы векторы болғандықтан, * =A*l+ B*m=0

Жеткіліктілік. Al+bm=0 болсын. Сонда 0= Al+bm= * ↔ ||d

Яғни,анықтама бойынша s векторы d түзуінің бағыттаушы векторы болады.

Салдар. =(-B,A)векторы жалпы теңдеуімен анықталған d түзуінің бағыттаушы векторы болады. Шынында да, S=(-B,A) векторы үшін /4/-шарт орындалады.