- •Векторлар . Векторларды қосу амалы және оның қасиеттері (дәлелдеуімен)
- •2. Векторларды санға көбейту амалы және оның қасиеттері (дәлелдеуімен)
- •3. Сызықтық тәуелді векторлар жүйесі. Сызықтық тәуелді векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •4. Сызықтық тәуелсіз векторлар жүйесі. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •6. Компланар векторлардың анықтамасы. Үш вектордың компланар болу белгісі. (дәлелдеумен)
- •8. Вектордың векторлық проекциясы және оның қаситеттері.
- •9. Екі вектордың скаляр көбейтіндісі және оның қасиеттері
- •10. Скаляр көбейтіндіні тікбұрышты координаталар жүйесінде есептеу формулалары.
- •12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
- •13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.
- •Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
- •15. Жазықтықтағы түзудің нормал теңдеуін қорытып шығару.
- •17. Жазықтықтың теңдеулерілерін қорытып шығару.
- •19. Екі жазықтықтың өзара орналасуы. (дәлелдеумен)
- •20. Екі жазықтықтың арасындағы бұрыш.
- •21.Жазықтықтың нормаль векторы. Жазықтықтың нормал теңдеуін қорытып шығару. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық.
- •22. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың формуласын қорытып шығару.
- •24. Кеңістіктегі түзумен жазықтықтың өзара орналасуын зерттеу.
- •25. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыш.
- •26. Эллипс. Канондық теңдеу
- •29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)
- •33. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.
- •35. Векторлар жүйесінің базасы және рангі.
10. Скаляр көбейтіндіні тікбұрышты координаталар жүйесінде есептеу формулалары.
11. Векторлардың векторлық көбейтіндісі және оның геометриялық мағынасы. Егер а, b, с оң қолдың баспармақ , сұқ саусақ, ортаңғы саусақ тарға сәйкес орналасса, онда а, b, c үштігін оң деп атаймыз, кез келген 3 вектордан 6 үштік құрауға болады:
Егер үштікте 2 вектордың орнын ауыстырса, үштік атын өзгертеді,
a, b, c; a, c, b; …..
Анықтама. а және в векторының векторлық көбейтіндісі деп келесі шартты қанағаттандыратын с векторын айтамыз:
1) а, в, с-оң үштік
2)а перпендук с, в перпендукляр с
3)|с|=|[a,b]|=|a||b|sin(a,b) c=[a,b]
a,b векторларының векторлық көбейтіндісінің қасиеттері:
1)кез келген a,b [a,b]=-[b,a]
2 кез келген a,b кез келген α€IR [αa,b]=α[a,b]
3)[λa,b]=[a,λb]=λ[a,b]
4)[a,a]=0≠a2
Теоремасы : а={x1, y1, z1} b={x2, y2, z2}
Декарт координаттар жүйесінде а мен б-ның векторлық көбейтіндісі келесі формула бойынша есептеледі:
[a,b]=
Геометриялық мағынасы – сол вектордан құралған паралелограмның ауданына тең. S=|a||b|sin(a,b)=|[a,b]|
Теорема:Ө емес а, б вектор-ң векторлық көбейтіндісі 0-ге тең болады, сонда және сонда ғана егерде олар коллинеар. Коллениар векторлар арасындағы бұрыш 0 градусқа неемесе 180 градусқа тең.
[ ]=Ө
=>
– коллениар
]=Ө
=>
– коллениар
Д/У:
[
]=Ө
=> |[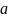 ,b]|=|a||b|sin(a,b)
=0
,b]|=|a||b|sin(a,b)
=0
 =Ө
немесе
=Ө
немесе
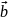 =Ө
нөлдік вектор кез келген векторға
коллениар.
=Ө
нөлдік вектор кез келген векторға
коллениар.sin(a,b) =0 => (a^b) = π немесе (a^b)=0 векторлар параллел онда олар коллениар.
12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
Үш вектордың аралас көбейтіндісі.Анықтама.Ретке келтірілген нөлдік емес a,b,c векторлары үштігінің аралас көбейтіндісі деп a*b векторымен c векторының скалярлық көбейтіндісіне тең санды айтады. Үш вектордың аралас көбейтіндісі a*b*c деп белгіленеді. Сонда, анықтама бойынша,а*b*c =(a*b)*c .
Егер a,b,с векторларының кем дегенде біреуі нөлдік вектор болса,онда аралас көбейтінді нөлге тең деп саналады.
Геометриялық мағынасы. 1-теорема. Компланар емес a,b,c векторларының көбейтіндісі ортақ бас нүктеден шыққан a,b,c векторларына салынған, егер a,b,c векторлар үштігі оң жақты болса,онда оң таңбамен,ал a,b,c үштігі сол жақты болса,теріс таңбамен алынған параллелепипедтің көлеміне тең болады. A,b,c векторлары компланар емес деп санап, мына екі жағдайды қарастырамыз. Алдымен, a,b,c үштігі оң жақты деп санайық.
А=OA, b=OB, c=OC векторларына салынған параллелепипедтің көлемін V арқылы белгілейік. Сонда V=S*h.
Мұндағы S a және b векторларына салынған параллелограмның ауданы,ал h=\OD\-параллепипедтің биіктігі. A*b=d деп белгілейік. Екі вектордың векторлық көбейтіндісінің анықтамасы бойынша;1\ \d\=s;
2\d векторы а және b векторлары жүргізілген жазықтығына перпендикуляр;
3\a,b,d векторлар үштігі оң жақты болады. Бұдан с және d векторлары жазықтығының бір жағында оорналасқандығы шығады,демек
OCD үшбұрышынан h=\c\*cosµ \1\
Енді d және с векторларының скаляр көбейтіндісін қарастырайық. Сонда ол бір жағынан d*c=(a*b)*c \2\
болса, ал екінші жағынан ,|d|=s теңдігі мен формуланы пайдалансақ,онда
d*c=|d|*|c|*cosµ=S*h=V \3\
болады,\2\ және\3\-формулалардың оң жақтарын теңестірсек,(a*b)*c=V болады.
Енді a,b,c векторлар үштігі сол жақты деп санайық. Сонда a*b=d және с векторлары α жазықтығының әртүрлі жағында жатады,демек,(c^,d)=µ>∏/2, яғни,соsµ< 0. OCD үшбұрышынан мына теңдік шығады. h=|c|*cosµ=|c|*cos(∏-µ)=-|c|*cosµ \4\
Егер |d|=S және \4\ формулаларын ескерсек,онда d*c=|d|*|c|*cosµ=S*(-h)=-S*h=-V \5\
Ал,егер a,b,c векторлар үштігі сол жақты болса, онда \2\ және \5\ формулалардан мына формуланы шығарып аламыз. (a*b)*c=-V. Сонымен, кез келген компланар емес a,b,c векторлар үштігі үшін V=|(a*b)c| формуласын аламыз.
Есептеy формаласы:
ТКЖ:a=(a1,a2,a3), b( b1,b2,b3)
i, j,k-орта нормаланған базис
[a,b]=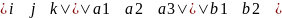 =i*|
=i*|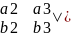 -j
-j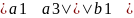 +K
+K
[a,b]=(a2b3-b2a3-a1b3+b1a3*a1b2-b1a2)
S=
C=(c1,c2,c3) a=(a1,a2,a3) b=(b1,b2,b3)
(a,
b ,c)=