30. Барометрическая формула. Распределение Больцмана.

При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям делалось предположение, что внешние силы не действуют на молекулы газа, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Сила тяжести, с одной стороны, и тепловое движение молекул — с другой, приводят газ к некоторому стационарному состоянию, при котором давление газа с высотой уменьшается.  Выведем закон изменения давления с высотой, предполагая при этом, что масса всех молекул одинакова, поле тяготения однородно и температура постоянна.

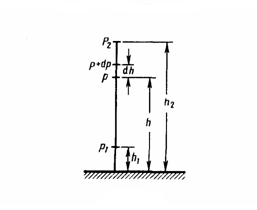
Рис.1 Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²:    где ρ — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом интервале плотность газа можно считать постоянной). Значит,   (1)  Зная уравнение состояния идеального газа pV=(m/M) RT (m — масса газа, М — молярная масса газа), находим, что    Подставив это выражение в (1), получим   или    С изменением высоты от h₁ до h₂ давление изменяется от р₁ до р₂ (рис. 67), т. е.    или   (2)  Выражение (2) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде   (3)  где р — давление на высоте h.  Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на применении формулы (3). Из этой формулы следует, что чем тяжелее газ, тем давление с высотой убывает тем быстрее.  Барометрическую формулу (3) можно преобразовать, если воспользоваться формулой p=nkT:    где n – концентрация молекул на высоте h, n₀ – то же, на высоте h=0. Так как M=m₀N_A (N_A – постоянная Авогадро, m₀ – масса одной молекулы), a R=kN_A, то   (4)  где m₀gh=P — потенциальная энергия молекулы в поле тяготения, т. е.   (5)  Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.  Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и , то распределение Больцмана (5) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

31. Среднее число столкновений и средняя длина свободного пробега молекул.

Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями.

За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости  . Если за это же время она испытает в среднем   столкновений с другими молекулами, то ее средняя длина свободного пробега   , очевидно, будет равна

(3.1.1)

Предположим, что все молекулы, кроме рассматриваемой, неподвижны. Молекулы будем считать шарами с диаметром d. Столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем или равном d от прямой, вдоль которой двигается центр рассматриваемой молекулы. При столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. Поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии.

Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. За секунду молекула проходит путь, равный   . Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадают внутрь ломаного цилиндра, имеющего суммарную длину   и радиус d. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным   Если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно

(3.1.2)

В действительности движутся все молекулы. Поэтому число столкновений за одну секунду будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной.

Предположение о неподвижности всех молекул, с которыми сталкивается рассматриваемая молекула, будет снято, если в формулу (3.1.2) вместо средней скорости <Vотн>представить среднюю скорость относительного движения <Vотн> рассматриваемой молекулы. В самом деле, если налетающая молекула движется со средней относительной скоростью <Vотн> , то молекула, с которой она сталкивается, оказывается покоящейся, что и предполагалось при получении формулы (3.1.2). Поэтому формулу (3.1.2) следует написать в виде:

(3.1.3)

Предположим, что скорости молекул до столкновения были   и   Тогда   

Из треугольника скоростей имеем (рис. 2) (3.1.4)

Так как углы   и скорости   и   , с которыми сталкиваются молекулы, очевидно, являются независимыми случайными величинами, то среднее

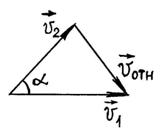рис. 2

от произведения этих величин равно произведению их средних. Поэтому

(3.1.5)

С учетом последнего равенства формулу (3.1.4) можно переписать в виде:

(3.1.6)

так как   Cредняя квадратичная скорость пропорциональна средней скорости,

(3.1.7)

т. е.   .

Поэтому соотношение (3.1.6) можно представить так:

(3.1.8)

С учетом последнего выражения формула для средней длины свободного пробега приобретает вид:

(3.1.9)

Для идеального газа   . Поэтому

(3.1.10)

Отсюда видно, что при изотермическом расширении (сжатии) средняя длина свободного пробега растет (убывает).

Как было отмечено во введении, эффективный диаметр молекул убывает с ростом температуры. Поэтому при заданной концентрации молекул средняя длина свободного пробега увеличивается с ростом температуры.

Вычисление средней длины свободного пробега для азота (d = 3•10^-10 м), находящегося при нормальных условиях (р = 1,01•10⁵ Па, Т = 273,15 К) дает:  , а для числа столкновений за одну секунду:   . Таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. Поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.