II. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка X отображается в такую точку , что .

Учитель: Постройте образ точки Х при осевой симметрии с осью l. Выделите для построения 10 клеток.

Ученики:

Учитель: Третьим пунктом выделим свойства параллельного переноса.

(Посередине страницы записывается заголовок: Свойства.) Вы доказали, что параллельный перенос является движением, запишем этот факт как первое свойство.

В тетрадях появляется запись: III. 1) Параллельный перенос является движением.

Учитель: Какой из этого следует вывод?

Ученики: Параллельный перенос обладает всеми свойствами движения. Он переводит отрезок в отрезок, луч - в луч, угол - в равный ему угол, любую фигуру в равную ей фигуру.

Учитель: Как вы думаете какие точки являются неподвижными при параллельном переносе?

Ученики: Неподвижных точек нет.

Учитель: Какая прямая называется неподвижной?

Ученики: Неподвижная прямая-это прямая, которая при движении отображается на себя.

Учитель: Какие прямые при параллельном переносе являются неподвижными?

Ученики: Неподвижных прямых нет.

Учитель: Запишем в таблицу второе свойство:

2) Неподвижных точек, неподвижных прямых - нет.

Построим образ прямой при параллельном переносе. Какие случаи взаимного расположения прямой и вектора параллельного переноса возможны?

Ученики: Прямая и вектор переноса могут быть параллельными или не параллельными.

Учитель: Рассмотрим случай, когда вектор переноса и прямая не параллельны. (Учитель строит прямую d, проходящую через точку Х). Постройте образ прямой d.

Ученики выполняют построения.

Что мы строим, чтобы найти образ прямой d? Почему?

Ученики: Мы строим образ точки У, лежащей на d. Потому, что образ прямой мы строим через образы двух точек, а образ точки Х, уже построен.

Учитель: Что мы можем сказать о взаимном расположение прямой d и её образа, обозначим его d₁?

Ученики: d параллельна d₁.

Учитель: Какой общий вывод мы можем сделать?

Ученики: Если прямая не параллельна вектору переноса, то ее образ параллелен самой прямой.

Рассмотрим случай, когда вектор переноса и прямая не параллельны. (Учитель строит прямую b). Постройте образ прямой b.

Учащиеся выполняют построения.

Как расположены прямая и её образ? Какой общий вывод мы можем сделать?

Ученики: Прямая b и b₁ совпадают. Если прямая параллельна вектору переноса, то ее образ совпадает с самой прямой.

Учитель: Запишем полученные факты в таблицу. (Учитель сам на доске записывает 3 свойство).

В тетрадях появляется запись:

3) 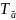(d)=d₁, (b)=b₁.

a)

б)

Учитель: Рассмотрим луч ХУ, на какой луч он отобразится при параллельном переносе?

Ученики: На луч Х₁У₁.

Учитель: Что мы можем сказать о взаимном расположение лучей ХУ и Х₁У₁?

Ученики: Лучи ХУ и Х₁У₁ сонаправлены.

Учитель: Сделаем общий вывод. На что при параллельном переносе отображается луч?

Ученики: Любой луч отображается на сонаправленный с ним луч.

Запишите это свойство в таблицу.

Учитель: приведем пример фигуры, которая отображается при параллельном переносе в себя.

Прямая, параллельная вектору , отображается на себя при параллельном переносе на вектор

3. Рефлексивно - оценочный этап.

Учитель: Давайте подведем итоги урока и проанализируем, какой новый материал вы сегодня узнали.

Ученики: Мы повторили определение и способ задания каждого частного вида движений. Ввели понятия неподвижных точек и прямых. Определили, какие точки и прямые являются неподвижными при каждом движении. Рассмотрели взаимное расположение прямой и её образа, привели примеры фигур, которые переходят при каждом из движении в себя.

Учитель: в начале урока мы решали задачу.

Задача: Даны два прямоугольных равнобедренных треугольника АОВ и СОD, они образуют четырехугольник АВСD, диагональ которого BD=d. Найдите площадь четырехугольника АВСD.

Учитель рассказывает учащимся решение, записи ведутся только на доске.

Решение: Рассмотрим поворот вокруг точки О на угол .

При этом повороте: (D)=C, (C)=B, (B)=A, (A)=D.

Следовательно (ВD)=СА. Так как поворот-это движение, значит он сохраняет расстояние между точками. Отсюда следует, что ВD=СА=d (по условию).

Угол между диагоналями четырехугольника равен углу поворота .

Следовательно зная длину диагоналей и величину угла между ними, мы можем найти площадь четырехугольника АВСD.

S _АВСD= .

Ответ: S _АВСD= .

Решение этой задачи опирается на свойства поворота. Далее на уроках мы будем решать подобные задачи, для этого вам нужно выучить таблицу, которую мы заполнили на уроке.

Домашнее задание:

Выучить теоретический материал по таблице, полученной в ходе урока.

21