26. Линейный коэффициент корреляции

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле^[10][8]:

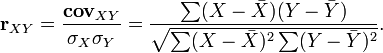
где ,  — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы^[11].

Доказательство

Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где — коэффициент регрессии, — среднеквадратическое отклонение соответствующего факторного признака^[12].

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).

27 Предмет физики

Физика — это наука о природе (естествознание) в самом общем смысле (часть природоведения). Она изучает различные субстанции бытия (материю, вещество, поля) и наиболее простые и вместе с тем наиболее общие формы её движения, а также фундаментальные взаимодействия природы, управляющие движением материи.

Некоторые закономерности являются общими для всех материальных систем, например, сохранение энергии, — их называют физическими законами. Физику иногда называют «фундаментальной наукой», поскольку другие естественные науки (биология, геология, химия и др.) описывают только некоторый класс материальных систем, подчиняющихся законам физики. Например, химия изучает атомы, образованные из них вещества и превращения одного вещества в другое. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, описываемыми в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика.

Физика тесно связана с математикой: математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений, причём используются более сложные разделы математики, чем обычно в других науках. И наоборот, развитие многих областей математики стимулировалось потребностями физических теорий (см. математическая физика).

28

Некоторые закономерности являются общими для всех материальных систем, например, сохранение энергии, — их называют физическими законами. Физику иногда называют «фундаментальной наукой», поскольку другие естественные науки (биология, геология, химия и др.) описывают только некоторый класс материальных систем, подчиняющихся законам физики. Например, химия изучает атомы, образованные из них вещества и превращения одного вещества в другое. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, описываемыми в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика.

Физика тесно связана с математикой: математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений, причём используются более сложные разделы математики, чем обычно в других науках. И наоборот, развитие многих областей математики стимулировалось потребностями физических теорий

29

30 Среди разнообразных колебательных движений отдельное место занимают гармонические колебания. При таких колебаниях физические величины, описы- вающие эти движения (например, отклонение от состояния равновесия, скорость, ускорение и т.д.), изменяются с течением времени по закону косинуса или синуса. Этот вид колебаний особенно важен потому, что в соответствии с учением о ко- лебаниях любые периодические колебания, которые наблюдаются в природе и тех- нике, можно представить как наложение нескольких гармонических колебательных движений. Таким образом, гармонические колебания являются простейшим видом колебательного движения. Рассмотрим колебания, которые происходят под воздействием упругой силы. Для этого используем колебательную систему, состоящую из массивного шара с отверстием, насаженного на горизонтальный стержень, вдоль которого он может скользить с ничтожно малым трением. На стержень надета стальная пружина, за-

Кафедра общей и теоретической физики Профессор В.А. Яковенко крепленная на его конце и на шаре (рис. 22.1). Массой пружины будем пренебрегать. В положении O шар находится в состоянии покоя. При этом пружина не деформирована (рис. 22.1, а). Сместим шар из состояния равновесия вправо (рис. 22.1, б) на ма- лый отрезок OB, а затем отпустим. В результате он начнет ускоренно двигаться влево под действием упругой силы пружины F kx =−  , где x  – вектор смещения шара из состояния равновесия. Знак «минус» обозначает, что сила направлена в сторону, противоположную вектору смещения, т.е. к состоянию равновесия. Под действием упругой силы пружины шар начнет двигаться к состоянию рав- новесия со все большей и большей скоростью. Численное значение упругой силы при этом будет уменьшаться и в точке O станет равным нулю. За счет запаса кине- тической энергии шар минует состояние равновесия и будет продолжать двигаться влево, растягивая пружину. В результате на него начнет действовать упругая сила, направленная вправо. Под действием этой силы шар будет тормозить до того вре- мени, пока вся кинетическая энергия не преобразуется в потенциальную энергию пружины. Остановившись на мгновение, он под действием упругой силы, которая достигнет максимального значения, начнет двигаться назад к состоянию равнове- сия O и т.д. Колебания, происходящие в системе при отсутствии внешних воздействий по- сле какого-нибудь начального отклонения ее от состояния равновесия, называются свободными или собственными. Если в системе отсутствует переход механиче- ской энергии в другие ее виды (консервативная система), то свободные колебания будут незатухающими. В любой реальной колебательной системе часть энергии колебательного движения всегда расходуется на преодоление сил сопротивления, и колебания постепенно затухают. Покажем, что свободные незатухающие колебания, которые происходят под действием упругой силы, являются гармоническими. Уравнение второго закона Ньютона для колеблющегося шара ma kx =− , Рис. 22.1

Кафедра общей и теоретической физики Профессор В.А. Яковенко где a – ускорение шара. Ускорение a, равное второй производной смещения x по времени, обозначим: ax =. Подставляя в формулу вместо a его значение, получим mx kx =− , или k xx m =− . Поскольку k и m – величины положительные, то их отношение приравняем квадрату некоторой величины 0 ω

2 0 k m =ω. После этого последнее уравнение примет вид: 2 0 0 xx +ω = . Как видим, колебания шара под действием упругой силы описываются одно- родным линейным дифференциальным уравнением второго порядка. Решение это- го уравнения должно давать возможность определить смещение x как функцию времени t. Легко проверить, что общим решением этого уравнения будет функция: ( ) ( ) 00 01 cos sin , x A t или x A t  = ω +α   = ω +α   (*) где A и 0 α – постоянные величины, которые зависят от начальных условий; 10 2 α =α +π . Таким образом, смещение из состояния равновесия x изменяется с течением времени по гармоническому закону, что позволяет сделать вывод, что движение системы под действием упругой силы F kx =−   является гармоническим колебани- ем. Полученные уравнения называются уравнениями гармонического колебатель- ного движения. Перейдем к их исследованию.

31

Среди возможных движений сплошной среды выделяется волновое движение, которое в большинстве случаев можно интерпретировать, как последовательное перемещение значений физических величин, заданных в некоторый (начальный) момент времени в определенных точках пространства от одной точки к другой. Представление о волновом движении в простейшем случае иллюстрируется одномерным движением. Пусть при 0 t в некоторой области пространства l x0 задано начальное распределение физической величины (например, плотности массы) с помощью функции:     xfx  0, . Движение называется волновым, если с течением времени изменение распределения плотности можно интерпретировать, например, как смещение начального распределения в положительном направлении оси OX :     Vtxftx  , . В рассматриваемом случае смещение пропорционально времени. Коэффициент пропорциональности называется (фазовой) скоростью волны. Если начальное распределение задано дифференцируемой функцией, то нетрудно найти дифференциальное уравнение (в частных производных), которому удовлетворяет данное волновое движение среды:    t V x   0. (1) Полученное уравнение называется уравнением простой волны.

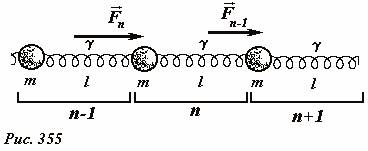
Теперь с помощью полученных кинематических законов рассмотрим энергетические характеристики волны, распространяющейся по цепочке. Мысленно разобьем цепочку на одинаковые элементарные ячейки, включающие шарик и следующую за ним пружину (Рис. 355).

Кинетическая энергия одной ячейки совпадает с кинетической энергией движущегося шарика, ее зависимость от времени выражается формулой

 Wkin,n=mυ2n2=mA2ω22sin2(ωt−nΔφ) . (13)

Во многих случаях основной интерес представляет среднее значение кинетической энергии, которое легко определить из выражения (13)

 <Wkin,n>=<mA2ω22sin2(ωt−nΔφ)>=mA2ω24 , (14)

где учтено, что среднее значение квадрата синуса равно  12. Причем, особо отметим, что в данном случае усреднение можно понимать двояко: как усреднение по промежутку времени, значительно превышающему период колебаний; либо как усреднение по участку цепочки, длина которого значительно превышает длину распространяющейся волны. В первом случае мы, как бы, следим за движением одного шарика в течение некоторого промежутка времени; во втором – рассчитываем среднюю энергию большого числа шариков в заданный момент времени. В случае гармонической волны такие усреднения временное и пространственное приводят к одному результату.

При переходе к непрерывному пределу от цепочки к непрерывной струне удобной характеристикой является средняя плотность энергии – энергия, приходящаяся на единицу длины струны^[3]. Для расчета этой характеристики следует среднюю энергию одной ячейки (14) разделить на ее длину

 <wkin,n>=<Wkin,n>l=ρA2ω24 , (15)

где обозначено  ρ=ml - средняя плотность цепочки, масса единицы длины.

Проведем расчет потенциальной энергии выделенной ячейки, то есть энергию пружинки, которая пропорциональна квадрату ее деформации

 Un=γ(un+1−un)22 . (16)

Из этой формулы следует, что потенциальная энергия ячейки зависит от разности смещений двух соседних шариков. Эту разность удобно выразить с помощью формулы (11)

 Un=γ2(−lcυn)2=γl22c2υ2n=mυ2n2=Wkin . (17)

Полученный результат является неожиданным: в любой момент времени потенциальная энергия ячейки равна ее кинетической энергии. Этот же вывод справедлив и для средней плотности потенциальной энергии

 <wpot,n>=<Un>l=γl22c2<υ2n>=γl4A2ω2c2=ρA2ω24 . (18)

Вспомните: при колебаниях маятника (как пружинного, так и математического) потенциальная энергия максимальна, когда кинетическая равна нулю, и наоборот - колебания этих двух видов энергии происходят в противофазе. В упругой волне эти колебания синфазны. Это принципиально различное поведение качественно может быть объяснено следующим образом: для пружинного маятника потенциальная энергия определяется его собственным смещением от положения равновесия, а для упругой волны эта энергия зависит от разности смещений двух соседей. Можно также указать, что для непрерывной среды ее кинетическая энергия пропорциональна производной от смещения по координате  υ=∂u∂t, а ее относительная деформация равна производной по координате  ε=∂u∂x. В случае незатухающей волны эти производные изменяются со временем по одному закону, следовательно, одинаково изменяются кинетическая и потенциальная энергии.

Суммарная средняя плотность энергии упругой волны определяется по формуле

 <w>=<wkin,n>+<wpot,n>=ρA2ω22 , (19)

она пропорциональна квадрату амплитуды волны и квадрату ее частоты.

Приведем еще одно выражение для плотности потенциальной энергии. Выразим потенциальную энергию пружинки через ее относительную деформацию  εn=u(n+1)−unl:

 Un=γ(un+1−un)22=γl2ε2n2 .

Теперь средняя потенциальная энергия оказывается равной

 wpot,n=Unl=γl2ε2n2=Eε22 ,

где E = γl - введенный ранее модуль Юнга среды. Сравните полученное выражение с формулами для средних плотностей энергии электрического и магнитного полей!