1.4.2. Дробные реплики

Число опытов в полном факторном эксперименте быстро возрастает с ростом числа факторов. Так, при трех факторах будем иметь 2³=8 опытов, при 5 факторах - 2⁵=32 опыта, а при 8 факторах уже 2⁸=256 опытов. Это вызывает необходи­мость разработки методов отбора части переменных, наиболее существенно влияющих на поверхность отклика. Поэтому, хотя полный факторный план 2^k является удобным с точки зрения простоты проведения анализа параметров функции регрессии, тем не менее при большом числе факторов его применяют редко. При трех и более факторах количество опытов можно существен­но сократить за счет потери части информации, не очень сущест­венной при построении линейных моделей. Для этого вместо плана 2^k следует использовать дробный фактор­ный план 2^{k - p} (2^{k - p}≥+1), который предназначен для реализации 2^{k -p} опытов. Для построения дробных планов (реплик) использу­ют матрицы полного факторного эксперимента. Дробные планы создают делением числа опытов полного факторного экспериме­нта на число, кратное двум. Так получают 1/2 реплики (полуреп­лику), 1/4 реплики (четвертьреплику) и т. д.

Вначале рассмотрим линейную функцию регрессии, завися­щую от трех факторов:

(1.67)

Для оценки четырех коэффициентов b₀, b₁, b₂, b₃ требуется провести четыре опыта, а проведение полного факторного экс­перимента, состоящего из восьми опытов, позволяет несмещенно оценить не только общее среднее b₀ и главные эффекты b₁, b₂, bз, но также и всевозможные взаимодействия первого и второго порядков, т. е. все параметры неполной кубической модели

(1.68)

содержащей восемь коэффициентов. Следовательно, восемь опы­тов, поставленных для оценки коэффициентов линейной модели (1.67), будут содержать в два раза больше информации, чем требуется.

Для оценивания параметров функции регрессии (1.67) можно построить план, предназначенный для проведения не восьми, а четырех опытов. Для этой цели факторы x₁ и х₂ следует варьировать, как в плане 2², а в качестве уровня фактора х₃ нужно выбрать значение взаимодействия, т. е. х₃ = x₁x₂. Получим план, определяемый матрицей, приведенной в табл. 1.4.

Таблица 1.4

№ опыта	Матрица плана
	x0	x1	x2	x3
1 2 3 4	+ 1 + 1 + 1 + 1	+ 1 - 1 + 1 - 1	+ 1 + 1 - 1 - 1	+ 1 - 1 - 1 + 1

Рассмотрим вопрос построения дробных реплик более под­робно. Вернемся к функции регрессии (1.68). Матрица плана этой модели приведена в табл. 1.5.

Рассмотрим эту таблицу более внимательно и обратим вни­мание, что второй столбец таблицы совпадает с девятым, тре­тий - с восьмым, четвертый - с седьмым, пятый - с шестым. Следовательно, при использовании этого плана нет различий между х₀ и х₁ х₂ x₃; x₁ и х₂ х₃; х₂ и x₁ x₃; х₃ и x₁x₂, т. е.

(1.69)

Таблица 1.5

№	Матрица плана
опыта	x0	x1	x2	x3	х1 x2	x1 x3	x2 x3	x1 x2 x3
1	2	3	4	5	6	7	8	9
1 2 3 4	+1 +1 +1 +1	+1 -1 +1 -1	+1 +1 -1 -1	+1 -1 -1 +1	+1 -1 -1 +1	+ 1 +1 -1 -1	+1 -1 +1 -1	+1 +1 +1 +1

На этом основании можно утверждать, что вместо отыскания оценок восьми параметров функции регрессии (1.68) можно найти оценки лишь четырех смешанных коэффициентов:

(1.70)

При этом главные эффекты, включая общее среднее, оценивают­ся независимо друг от друга, но смешиваются соответственно с эффектами взаимодействий второго и первого порядка. Если постулируется линейная модель (1.67), то эффекты взаимодейст­вий считаются незначительными, а смешанные коэффициенты (1.70) превращаются в параметры модели (1.67).

Таким образом, полный факторный эксперимент 2³ при по­стулировании линейной модели можно рассматривать как сово­купность двух полуреплик. Представленный в табл. 1.5 план называют полурепликой или планом 2^{3 -1}, полученным из полно­го факторного плана 2³ путем приравнивания единице произведе­ния x₁ x₂ x₃, т. е.

(1.71)

Это соотношение называется определяющим для данной полуреп­лики. Другая полуреплика 2^{3 -1} получится из определяющего соотношения x₁ x₂ x₃ = - 1, т. е. если уровни фактора х₃ устанавли­вать в соответствии с равенством х₃= - x₁ x₂.

Пример. План полного факторного эксперимента и его результаты записаны в левой части (столбцах 1...6) табл. 1.6. Требуется составить уравнения регрессии для полного факторного эксперимента и для его дробных реплик, если известно, что функция отклика линейна (либо постулируется ее линейность).

Таблица 1.6

№ опыта					y
1	2	3	4	5	6	7	8	9	10
1	+1	-1	-1	-1	4	+1	+1	+1	-1
2	+1	+1	-1	-1	16	-1	-1	+1	+1
3	+1	-1	+1	-1	-4	-1	+1	-1	+1
4	+1	+1	+1	-1	8	+1	-1	-1	-1
5	+1	-1	-1	+1	8	+1	-1	-1	+1
6	+1	+1	-1	+1	20	-1	+1	-1	-1
7	+1	-1	+1	+1	0	-1	-1	+1	-1
8	+1	+1	+1	+1	12	+1	+1	+1	+1

Решение. Запишем уравнение регрессии для линейной поверхности отклика

(1.72)

Коэффициенты b_i будем определять по формуле (1.62) в соответствии с приемами, указанными в пояснениях к этой формуле.

Вначале определим коэффициенты регрессии, используя данные полного фак­торного эксперимента (левую часть табл. 1.6).Имеем:

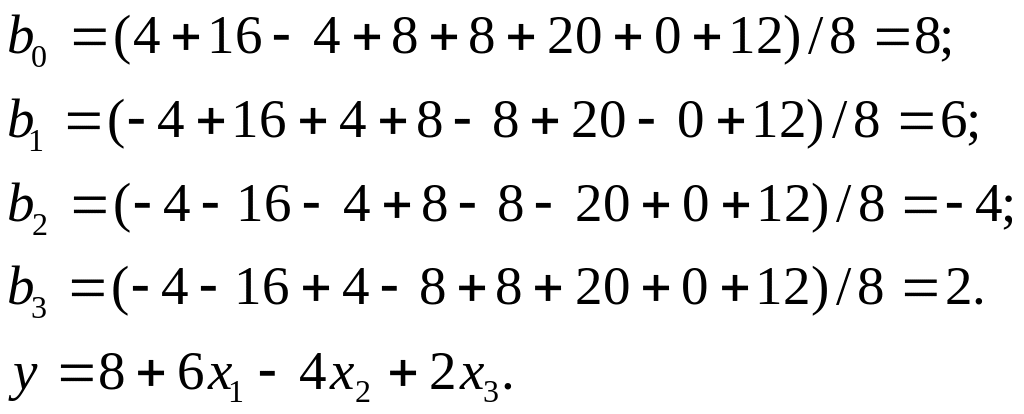(1.73)

Построим дробные реплики, для чего заполним правую часть табл. 1.6 (столбцы 7...10) и выберем строки, у которых 10-й столбец имеет одинаковые знаки. В результате получим две полуреплики:

Таблица 1.7

№ опыта	x0	x1	x2	x3	Y
1	2	3	4	5	6
Первая			Полуреплика
2	+ 1	+1	-1	-1	16
3	+ 1	-1	+1	-1	-4
5	+ 1	-1	-1	+1	8
8	+ 1	+1	+1	+1	12
Вторая полуреплика
1	+ 1	-1	-1	-1	4
4	+ 1	+1	-1	-1	8
6	+ 1	+1	-1	+1	20
7	-1	-1	+1	+1	0

Определим коэффициенты регрессии по дробным репликам.

Для первой полуреплики будем иметь: b₀ = (16—4+8-12)/4=8; b₁ = (16+4 — -8 + 12)/4 = 6; b₂ = (-16-4-8 + 12)/4=-4; b₃ = (-16 + 4+8-(-12)/4=2. Для вто­рой полуреплики b₀=(4+8+20+0)/4=8; b₁ = (-4 + 8+20-0)/4=6; b₂ = (-4 + + 8-20 + 0)/4=-4; b₃ = (-4-8 + 20)/4 = 2.

Как и следовало ожидать, во всех трех случаях для линейной поверхности отклика получены одинаковые результаты.

На рис. 1.20 приведена схема полного трехфакторного эксперимента и его полуреплик. Цифрами отмечены номера опытов с указанием в скобках координат факторов x₁, x₂, х₃. Точки 2, 3, 5, 8 соответствуют первой полуреплике, а цифры 1, 4, 6, 7 - второй. Обратите внимание, что каждая из полуреплик наиболее полно охватывает опытные точки факторного пространства.

При большом числе факторов т для оценивания параметров линейной функции регрессии (1.65) можно строить дробные репли­ки высокой степени дробности [19]. Так, при т = 7 можно постро­ить дробную реплику из полного факторного плана 2³ для пер­вых трех факторов, приравняв четыре остававшихся фактора к двухфакторным и трехфакторному взаимодействиям трех дру­гих факторов, положив, например

(1.74)

Такую реплику записывают как 2^{7 - 4}.

Рис. 1.20. Схема трехфакторного эксперимента

В общем случае дробную реплику обозначают через 2^{т - p}, если р факторов приравнены к произведениям остальных т - р фак­торов, уровни которых выбраны согласно полному факторному плану. Дробную реплику 2 ^{т - р} можно строить различными спо­собами. Для анализа системы смешивания коэффициентов пользуются понятиями генерирующих и определяющих соотно­шений.

Генерирующими называют соотношения, с помощью которых построена дробная реплика. Так, для реплики, представленной в табл. 1.5, генерирующим является соотношение x₃ = x₁x₂, а это указывает, что фактор х₃ занимает в матрице столбец, соответст­вующий взаимодействию х₁х₂. Для указанной выше реплики 2^{7 - 4}генерирующим является соотношение (1.74).

Определяющим соотношением (определяющим контрастом) называют равенство, в левой части которого стоит единица, а в правой — какое-либо произведение факторов. Для дробной реплики 2^{т - р} можно получить р различных определяющих соот­ношений из генерирующих путем умножения обеих частей по­следних на их левые части с последующей заменой (x_i)² на 1 (i=1,..,т). Другие определяющие соотношения получаются путем перемножения ранее полученных и выделения среди них новых. Например, для реплики (табл. 1.5) определяющим является соот­ношение (1.71).

Построим определяющие соотношения для реплики 2^{7 - 4}, за­даваемой генерирующими соотношениями (1.74). Умножая обе части равенств (1.74) на их левые части, получаем четыре опреде­ляющих соотношения:

(1.75)

Попарное перемножение этих четырех соотношений дает шесть новых:

(1.76)

Перемножение каждой тройки из четырех соотношений (1.75) дает еще три определяющих соотношения:

(1.77)

Наконец, перемножая все четыре соотношения (1.75), получаем

(1.78)

Легко понять, что кроме (1.75)...(1.78), других определяющих соотношений для рассмотренной реплики 2^{+ 7 - 4} нет.

Знание определяющих соотношений позволяет найти всю си­стему совместных оценок без изучения матрицы планирования дробной реплики. Для того чтобы определить, с какими взаимо­действиями смешано данное, нужно на него умножить обе части всех определяющих соотношений.

Определим, например, с какими взаимодействиями смешан главный эффект b₃ в дробной реплике 2^{7 - 4}, определяемой генери­рующими соотношениями (1.74). Для этого умножим все опреде­ляющие соотношения (1.75)...(1.78) на х₃. Получим

Следовательно, главный эффект b₃ смешан с эффектами вза­имодействий первого порядка

с эффектами взаимодействий второго порядка

третьего порядка

четвертого порядка

и пятого порядка

В конкретной практической ситуации для выбора подходящей дробной реплики полного факторного плана необходимо исполь­зовать все априорные сведения теоретического и интуитивного характера об объекте планирования с целью выделения тех фак­торов и произведений факторов, влияние которых на результаты измерений существенно. При этом смешивание нужно произво­дить так, чтобы общее среднее b_o и главные эффекты b₁, ..., b_т были смешаны с эффектами взаимодействий самого высокого порядка (так как обычно они отсутствуют) или с эффектами таких взаимодействий, о которых известно, что они оказывают несущественное влияние на результаты измерений. Отсюда сле­дует, в частности, что недопустимо произвольное разбиение пол­ного факторного плана 2³ на две части для выделения полурепли­ки 2^3-1.

Качество дробного факторного плана иногда характеризуют с помощью разрешающей способности плана, которая равна на­именьшему числу символов в правых частях определяющих соот­ношений. В частности, для плана разрешающей способности III ни один главный эффект не смешан ни с каким другим главным эффектом, но главные эффекты смешаны с эффектами двухфакторных взаимодействий. Для плана разрешающей способности IV главные эффекты не смешаны друг с другом и с эффектами двухфакторных взаимодействий, но последние друг с другом смешаны. Для плана разрешающей способности V главные эф­фекты и эффекты двухфакторных взаимодействий не смешаны, но последние смешаны с эффектами трехфакторных взаимодейст­вий. Все три рассмотренные выше дробные реплики имеют раз­решающую способность III.