1.4.1. Полный факторный эксперимент

Изложение основ факторного планирования эксперимента на­чнем с простейшего примера.

Пусть имеется две входные переменные и , одна из которых в интересующей нас области, заштрихованной на рис. 1.19 изменяется в пределах 0,4≤ ≤0,8, а другая - в пределах 10≤ ≤30. В процессе проведения эксперимента найдены значе­ния ординат поверхности отклика в граничных точках (рис. 1.19), приведенные в табл. 1.1.

Таблица 1.1

№ точки (опыта)			y
1 2 3 4	0,4 0,8 0,4 0,8	10 10 30 30	38 68 32 62

Поставим задачу поиска аналитического выражения функции отклика в линейной постановке, т. е. дадим приближенное пред­ставление этой функции в виде:

(1.60)

Для формализации процедур обработки экспериментальных данных факторы удобно представлять в закодированном виде. С этой целью выберем новую систему координат х₁ х₂ у (рис. 1.19 б), начало которой совместим с центром интересующей нас области, и назначим масштабы по осям факторов так, чтобы нижний уровень фактора соответствовал -1, а верхний - +1. Это легко достигается с помощью преобразований вида

(1.61)

где x_i, - кодированное значение i-го фактора; X_i - натуральное значение фактора; X₀ - нулевой уровень; ∆X_i - интервал варьи­рования фактора.

Для фактора Х₁ нулевой уровень и интервал варьирования будут равны

X₁₀ = (0,4 + 0,8)/2 = 0,6; ∆X₁= (0,8-0,4)/2 = 0,2. Для фактора Х₂ имеем:

X₂₀ = (10 + 30)/2 = 20; ∆X₂ = (30-10)/2 = 10.

Таблица 1.2

№ опыта	x0	x1	x2	y
1	2	3	4	5
1 2 3 4	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	38 68 32 62

Кодированные значения факторов приведены в табл. 1.2. В первом и пятом столбцах этой таблицы повторены значения табл. 1.1. Во втором столбце приведены значения фиктивной переменной х₀, характеризующей свободный член b₀ в уравнении регрессии (1.60). Значения х₀ всегда принимают равными 1. В 3 и 4 столбцах записаны искомые кодированные переменные; так, для фактора Х₁ в первой точке кодированное значение будет x₁₁ = (0,4 - 0,6)/0,2= - 1. Подобные таблицы называют матрица­ми планирования полного факторного эксперимента.

Все дальнейшие вычисления полностью формализованы. Ко­эффициенты регрессии уравнения (1.60) определяют по формуле

(1.62)

где x_in - значение х_i, в n-ом опыте; N - число опытов; у_п - значение отклика в п-ом опыте. Для вычисления коэффициентов регрессии по табличным данным достаточно перемножить данные столбцов у и соответствующих x_i сложить результаты и поделить их на число опытов.

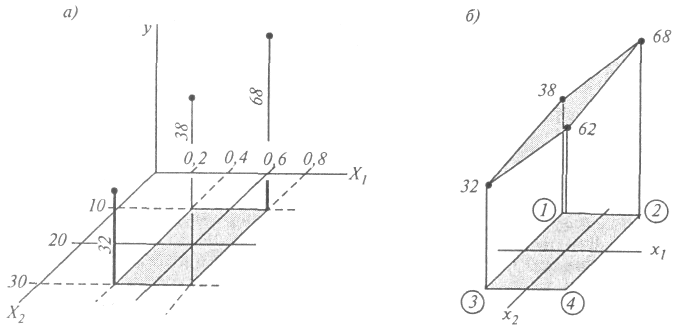
Рис. 1.19. Полный факторный эксперимент

Так, по данным табл. 1.2 имеем:

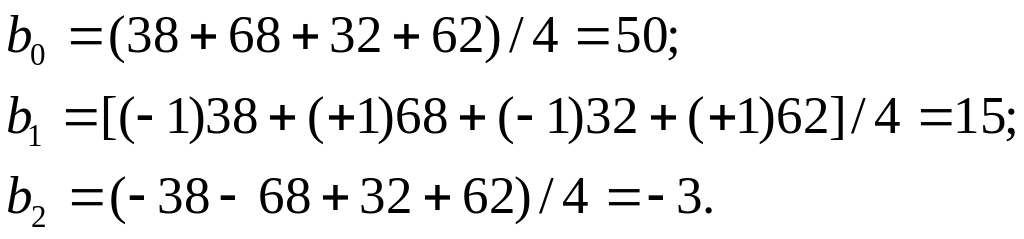
Искомое линейное уравнение поверхности отклика в закодиро­ванных переменных будет:

В натуральной (не кодированной) форме это уравнение име­ет вид:

(1.63)

Рассмотренный в примере план эксперимента соответствует двум факторам для линейной функции. Если поверхность откли­ка нелинейна, а мы пытаемся представить ее приближенное выра­жение, то в уравнении регрессии (1.60) следует добавить член b₁₂ x₁ x₂, учитывающий взаимодействие факторов х₁ и х₂. В нашем случае линейной исходной поверхности отклика этот член будет равен нулю, в чем нетрудно убедиться, добавив 6-й столбец, элементы которого равны произведениям элементов 3-го и 4-го столбцов.

В общем случае многофакторного эксперимента уравнение регрессии имеет вид:

(1.64)

Параметр b₀ называют общим средним, параметры b_i - главными эффектами (взаимодействиями нулевого порядка), параметры b_ij - эффектами взаимодействия первого порядка (эффектами двухфакторных взаимодействий), параметры b_ijk - эффектами взаимодействий второго порядка (эффектами трехфакторных вза­имодействий) и аналогично b_123…n - эффектами взаимодействия порядка n-1 (эффектами n-факторных взаимодействий).

Наиболее часто используют два частных случая функции рег­рессии (1.64): линейную

(1.65)

и неполную квадратичную

(1.66)

Техника эксперимента с варьированием k факторов на двух уровнях сводится к проведению 2^k опытов. Для построения мат­рицы планирования эксперимента при любом k следует дважды повторить матрицу планирования для случая k - 1: один раз для нижнего уровня k-го фактора, а другой раз - для верхнего. Последовательность достраивания матриц планирования при увеличении k от двух до пяти показана в табл.1.3. Первые четыре (отчеркнутые) опыта соответствуют двухфакторному экспери­менту типа 2², повторяя табл.1.2. Восьмифакторный план типа 2³ дважды повторяет двухфакторный эксперимент при варьиро­вании третьего фактора сначала на нижнем, а затем на верхнем уровнях. Аналогично строят планы полных факторных экспери­ментов при других значениях k.

Таблица 1.3

№
1	+1	-1	-1	-1	-1	-1
2	+1	+1	-1	-1	-1	-1
3	+1	-1	+1	-1	-1	-1
4	+1	+1	+1	-1	-1	-1
5	+1	-1	-1	+1	-1	-1
6	+1	+1	-1	+1	-1	-1
7	+1	-1	+1	+1	-1	-1
8	+1	+1	+1	+1	-1	-1
9	+1	-1	-1	-1	+1	-1
10	+1	+1	-1	-1	+1	-1
11	+1	-1	+1	-1	+1	-1
12	+1	+1	+1	-1	+1	-1
13	+1	-1	-1	+1	+1	-1
14	+1	+1	-1	+1	+1	-1
15	+1	-1	+1	+1	+1	-1
16	+1	+1	+1	+1	+1	-1
17	+1	-1	-1	-1	-1	-1
18	+1	+1	-1	-1	-1	-1
19	+1	-1	+1	-1	-1	-1
20	+1	+1	+1	-1	-1	-1
21	+1	-1	-1	+1	-1	-1
22	+1	+1	-1	+1	-1	-1
23	+1	-1	+1	+1	-1	-1
24	+1	+1	+1	+1	-1	-1
25	+1	-1	-1	-1	+1	-1
26	+1	+1	-1	-1	+1	-1
27	+1	-1	+1	-1	+1	-1
28	+1	+1	+1	-1	+1	-1
29	+1	-1	-1	+1	+1	-1
30	+1	+1	-1	+1	+1	-1
31	+1	-1	+1	+1	+1	-1
32	+1	+1	+1	+1	+1	-1

Выбор факторов. При проведении эксперимента факторы мо­гут быть управляемыми и неуправляемыми, наблюдаемыми и не­наблюдаемыми, изучаемыми и неизучаемыми, количественными и качественными, фиксированными и случайными.

Фактор является управляемым, если его уровни назначаются лицом, проводящим эксперимент, в соответствии с задачами исследования. В процессе эксперимента все управляемые фак­торы должны поддерживаться на заданном уровне или изменять­ся в соответствии с заданной программой.

Не всяким наблюдаемым (т. е. фиксируемым в процессе экс­перимента) фактором можно управлять. Такие наблюдаемые, но не управляемые факторы получили название сопутствую­щих. К ним относятся, в частности, воздействия внешней среды. Обычно сопутствующих факторов бывает довольно много, по­этому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на результаты экспери­мента.

После выбора факторов для каждого из них следует опреде­лить область, ограничивающую их возможное варьирование, и назначить основной уровень. Если, например, по условиям эксперимента нас интересует диапазон температуры воды от 20 до 60 °С, то основной уровень (для середины интервала) составит 40°, нижний уровень 20°, верхний уровень 60 °С. Разница значений между верхним и нижним уровнями фактора не может быть больше физически возможной. Например, для температуры обычной воды при нормальных условиях эта разность не может превысить 100 °С. При этом интервал варьирования не должен быть меньше ошибки фиксирования уровня фактора, иначе верх­ний и нижний уровни окажутся неразличимыми.

Факторы, которые по тем или иным причинам невозможно учесть в эксперименте, необходимо во всех опытах стабилизиро­вать на постоянных уровнях.