1.4. Планирование эксперимента

Планирование эксперимента позволяет оптимизировать тру­довые, временные и материальные затраты на проведение ис­следований, обеспечить их наиболее эффективное выполнение, а отсутствие соответствующего плана может существенно повы­сить трудоемкость исследований или сделать экспериментальную программу полностью безрезультатной.

Исторически теория планирования эксперимента начала раз­виваться с факторного планирования, основы которого зароди­лись еще в 30-х годах XX столетия. Основы этой теории состоят в построении экономичных планов, по результатам эксперимен­тальных измерений в точках которых можно делать статистичес­кие выводы о неизвестных параметрах функций регрессии, при­чем делать это на основе четко формализованных процедур. Факторное планирование включает построение полных и дроб­ных факторных планов, ортогональных латинских квадратов и сбалансированных блок-схем. В отличие от классического экс­перимента, в котором влияние различных значений входных переменных на результаты исследования рассматривается по одно­му, при факторном планировании эти значения одновременно комбинируются в разных вариантах. Это позволяет дать более точные оценки неизвестных параметров регрессии при равном числе измерений [19].

К настоящему времени сложилась стройная теория планиро­вания эксперимента, оперирующая с достаточно сложным мате­матическим аппаратом, имеющая свою терминологию. Рассмотрим основные положения этой теории, позволя­ющие организовать процесс моделирования не очень сложных систем. При этом ограничимся рассмотрением двухуров­невых планов, в которых влияние на результат эксперимента каждой из входных переменных изучается на двух уровнях, т. е. при наименьшем и наибольшем значениях этой переменной в пределах исследуемой области. Двухуровневые планы в силу ряда преимуществ получили наибольшее распространение при факторном планировании эксперимента.

Поскольку математические методы планирования экспериме­нта основаны на кибернетическом подходе, наиболее подходящей моделью эксперимента является «черный ящик», для которого известно лишь то, что подается на его вход, и то, что получается на выходе, а устройство этого ящика значения не имеет. Соответ­ственно мы будем иметь два типа переменных (входных и выход­ных), которые называют факторами и откликами. Для выясне­ния различий между ними рассмотрим простой эксперимент, в котором рассматриваются лишь две переменные х и у и целью которого является ответ на вопрос: как при изменении х будет изменяться y? В этом случае х - фактор, а у - отклик. В лите­ратуре встречаются другие термины: для фактора - режим, не­зависимая переменная, входная переменная, экзогенная перемен­ная; для отклика - реакция, выход, зависимая переменная, пере­менная состояния, эндогенная переменная. Подобная терминоло­гия возникла в связи с тем, что первые исследования с применени­ем статистических экспериментов проводились в сельском хозяй­стве, биологии, а затем стремительно вторгались в другие ниши, пополняясь там терминами, наиболее близкими и понятными читателям.

Каждый фактор х_i может принимать в эксперименте одно из нескольких значений, называемых уровнями. Каждому уровню соответствует определенная точка в многомерном пространстве, а множество таких точек образует поверхность отклика. На рис.1.19 показана поверхность отклика для двухфакторного экспери­мента. Факторами являются переменные х₁ и х₂. В точках 1, 2, 3, 4 эти факторы принимают определенные значения, которым отвечают соответствующие точки на поверхности отклика.

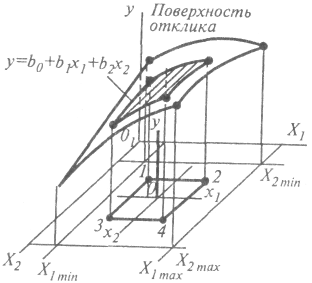
Рис. 1.19. Поверхность отклика.

(1.59)

Конфигурация поверхности отклика, следовательно, функция (1.59) не известна. Целью эксперимента является либо описание этой поверхности (хотя бы приближенное) в интересной для исследо­вателя области варьирования факторов, либо определение экст­ремального значения отклика. Вторая задача может быть сведена к пошаговому выполнению первой, поэтому на начальном этапе нас будет интересовать только поиск аналитического выражения, близкого к искомой функции (1.59) в заданной области. Этот поиск осуществляют на основе обработки экспериментальных данных в точках 1, 2, 3, 4 (см. рис. 1.19) факторного пространства.